Aufgabengruppe II - lernen mit Serlo!

Lösen Sie die folgenden Aufgaben.

Eine nach oben geöffnete Normalparabel $p_{1}$ verläuft durch die Punkte $A (– 2 | – 3)$ und $B (2 | 5)$ . Ermitteln Sie rechnerisch die Funktionsgleichung von $p_{1}$ in der Normalform.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für quadratische Funktionen
Die allgemeine Form oder auch Hauptform einer quadratischen Funktion lautet:
$f (x) = a x^{2} + b x + c$
Da es sich um eine nach oben geöffnete Normalparabel handelt ist der Vorfaktor $a = 1$
Setze die gegebenen Punktepaare in die Funktionsgleichung ein.
$\begin{array}{llrcl} Aus A (- 2 | - 3) : & I & - 3 & = & 1 \cdot (- 2)^{2} + b \cdot (- 2) + c \\ Aus B (2 | 5) : & I I & 5 & = & 1 \cdot (2)^{2} + b \cdot (2) + c \end{array}$
Berechnung der Parameter mit dem Gleichsetzungsverfahren;
$\begin{array}{llrcl} I & - 3 & = & 4 - 2 b + c \end{array} \Rightarrow c = 2 b - 7$
$\begin{array}{llrcl} I I & 5 & = & 4 + 2 b + c \end{array} \Rightarrow c = - 2 b + 1$
Setze $I = I I$
$2 b - 7$ $=$ $- 2 b + 1$
↓
fasse zusammen
$4 b$ $=$ $8$ $: 4$
$b$ $=$ $2$
Setze $2$ in $I$ oder $I I$ ein und berechne $c$ .
$c = 4 - 7 = - 3$
$c = - 3$
jetzt kannst Du die Funktionsgleichung aufstellen.
$p_{1} : y = x^{2} + 2 x - 3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Eine weitere Normalparabel $p_{2}$ hat die Funktionsgleichung $y = x^{2} - 5 x + 2,25$ . Bestimmen Sie rechnerisch die Scheitelpunktform und geben Sie den Scheitelpunkt $S_{2}$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Allgemeine Form und Scheitelform einer quadratischen Funktion
Umformen der allgemeinen Form in die Scheitelform:
$f (x)$ $=$ $y = x^{2} - 5 x + 2,25$
↓
Quadratische Ergänzung.
$=$ $x^{2} - 5 x + {(\frac{5}{2})}^{2} - {(\frac{5}{2})}^{2} + 2,25$
↓
In eine Binomische Formel umschreiben
$=$ ${(x - 2,5)}^{2} - {(\frac{5}{2})}^{2} + 2,25$
$=$ ${(x - 2,5)}^{2} - 4$
Jetzt kannst Du den Scheitelpunk ablesen: $S_{2} (2,5 | - 4)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Normalparabel $p_{2}$ schneidet die x-Achse in den Punkten $N_{1}$ und $N_{2}$ .
Berechnen Sie die x-Koordinaten dieser Nullstellen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Um die Schnittpunkte der Parabel mit der $x$ -Achse zu bestimmen, setze die Funktionsgleichung gleich $0$ und berechne $x$ z.B. mit der Mitternachtsformel.
$x_{1,2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
$x^{2} - 5 x + 2,25 = 0$
$x_{1,2} = \frac{5 \pm \sqrt{5^{2} - 4 \cdot 1 \cdot 2,25}}{2}$
$x_{1,2} = \frac{5 \pm \sqrt{25 - 9}}{2} \Rightarrow x_{1} = 4,5$
$x_{2} = 0,5$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Eine nach unten geöffnete Normalparabel $p_{3}$ hat den Scheitelpunkt $S_{3} (3 | 4) .$ Ermitteln Sie rechnerisch die Normalform der Funktionsgleichung von $p_{3}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Allgemeine Form und Scheitelform einer quadratischen Funktion
Der Scheitel der Parabel $p_{3}$ ist laut Angabe: $S_{3} (3 | 4)$
Die Scheitelform lautet:
$f (x) = a (x - d)^{2} + e$
Setze die entsprechenden Werte des Scheitels $S_{3}$ ein.
$p_{3} : y = - (x - 3)^{2} + 4$
die Normalform ist dann:
$p_{3} : y = - x^{2} + 6 x - 5$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
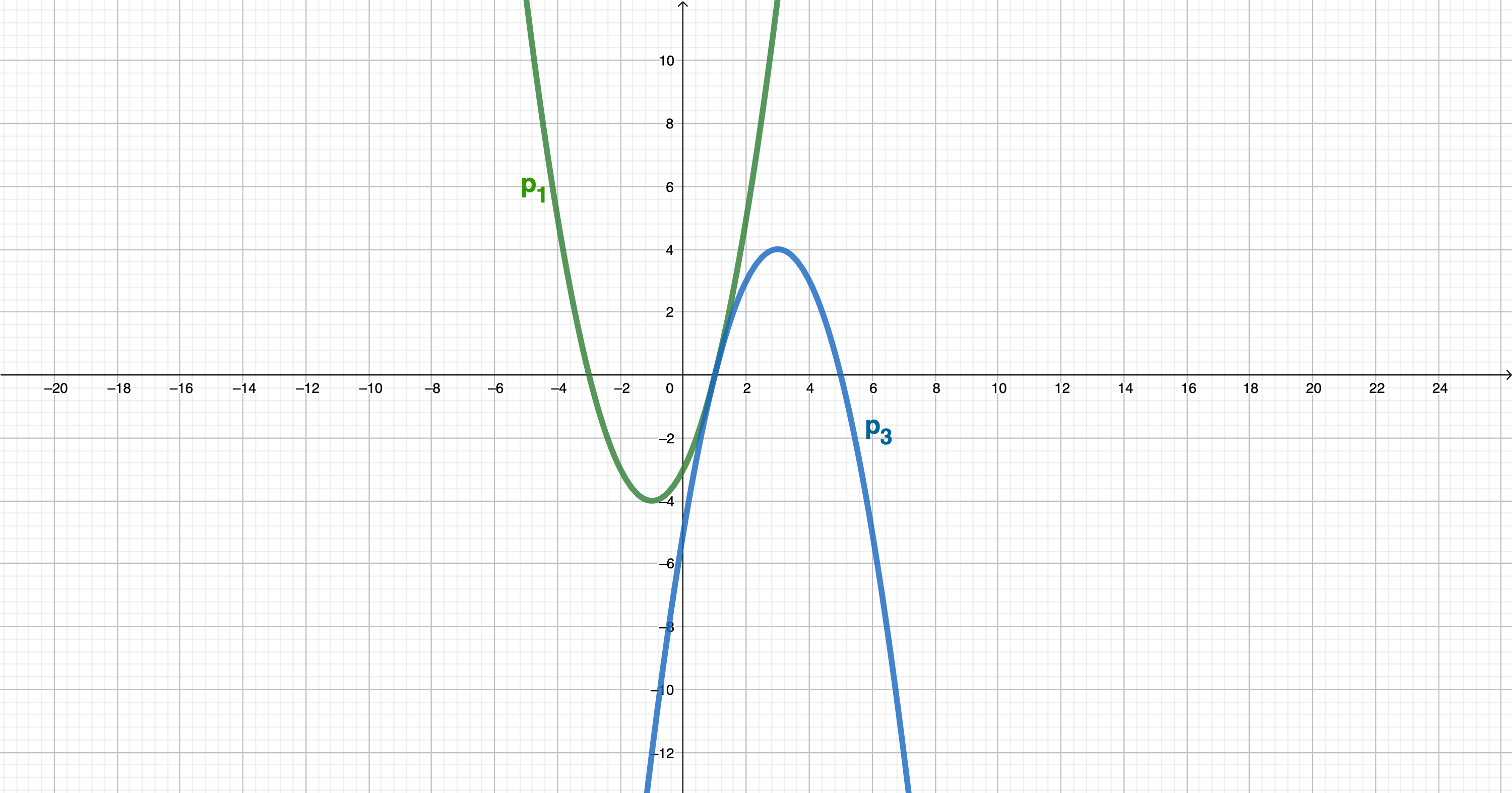
Zeichnen Sie die Normalparabeln $p_{1}$ und $p_{3}$ in ein Koordinatensystem mit der Längeneinheit 1cm.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel zeichnen
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überprüfen Sie nachvollziehbar, ob folgende Aussage richtig oder falsch ist:
Der Punkt $D (0 | 1)$ ist ein gemeinsamer Punkt der Normalparabel
$p_{4}$ : $y = (x – 2)^{2} – 3$ und der Geraden $g$ : $y = x – 3.$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Funktionen berechnen
Setze den $x$ Wert des Punktes D in die Geradengleichung $g : y = x - 3$ ein und berechne $y$ .
$y = 0 - 3 \Rightarrow y = - 3$
Die Gerade schneidet die $y$ -Achse bei $(0 | - 3)$ , also liegt $D$ nicht auf $g$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Normalparabel $p_{4}$ wird an der x-Achse gespiegelt. Geben Sie die Scheitelpunktform der so entstandenen Normalparabel $p_{5}$ an

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen spiegeln
Für die Spiegelung an der $x$ -Achse muss der Funktionsterm mit $(- 1)$ multipliziert werden.
$p_{4} : y = (x - 2)^{2} - 3 = \Rightarrow p_{5} : y = - 1 [\cdot (x - 2)^{2} - 3] = - 1 \cdot (x - 2)^{2} - 1 \cdot (- 3)$
Scheitelpunktform von $\begin{array}{l} p_{5} : \\ p_{5} : y = - (x - 2)^{2} + 3 \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$2 b - 7$	$=$	$- 2 b + 1$
	↓	fasse zusammen
$4 b$	$=$	$8$	$: 4$
$b$	$=$	$2$

$f (x)$	$=$	$y = x^{2} - 5 x + 2,25$
	↓	Quadratische Ergänzung.
	$=$	$x^{2} - 5 x + {(\frac{5}{2})}^{2} - {(\frac{5}{2})}^{2} + 2,25$
	↓	In eine Binomische Formel umschreiben
	$=$	${(x - 2,5)}^{2} - {(\frac{5}{2})}^{2} + 2,25$
	$=$	${(x - 2,5)}^{2} - 4$

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?