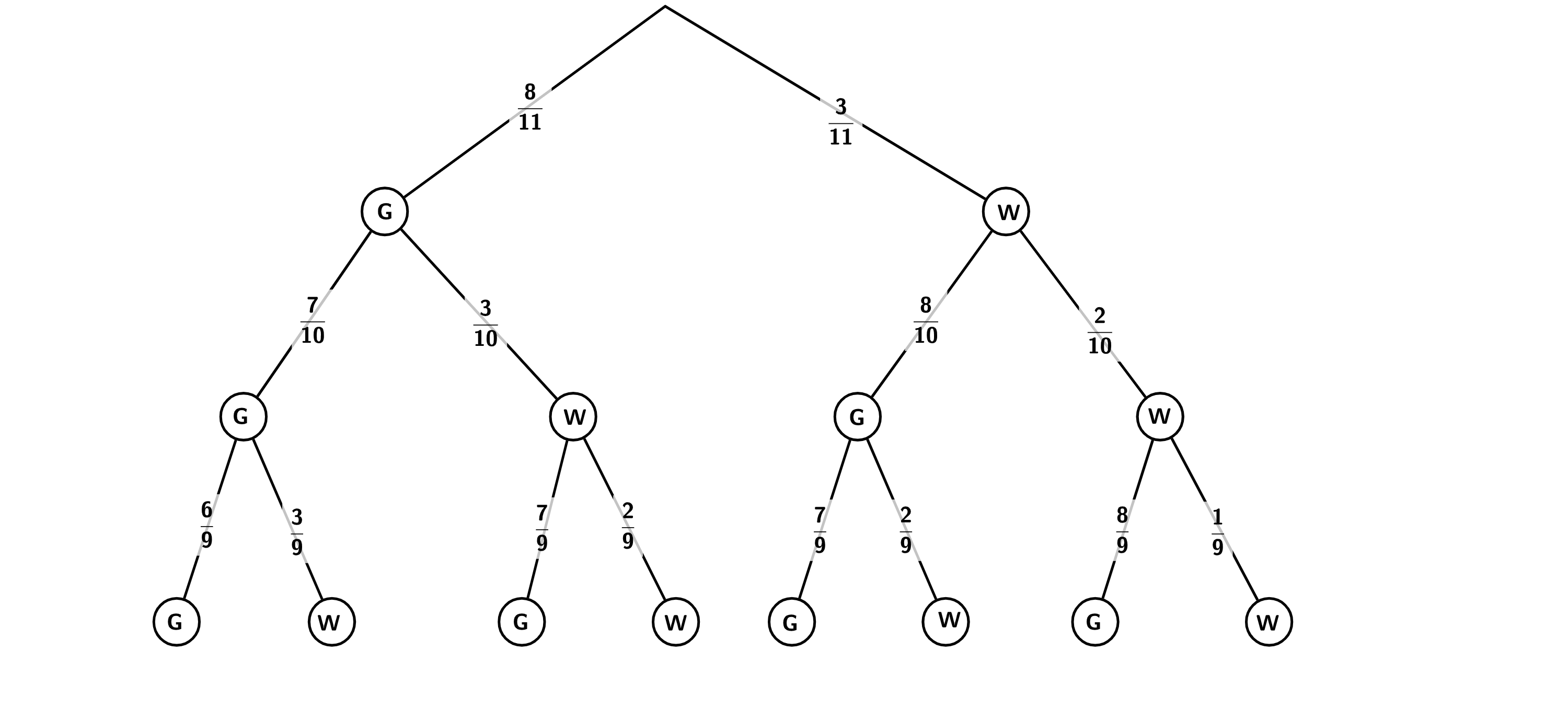
In einem Behälter befinden sich acht gelbe und drei weiße Spielbälle für ein Kickerturnier. Serkan nimmt nacheinander drei Spielbälle ohne Zurücklegen aus dem Behälter. Dies geschieht nach dem Zufallsprinzip.
Stellen Sie diesen Ablauf in einem Baumdiagramm dar und beschriften Sie die Äste mit den entsprechenden Wahrscheinlichkeiten.
Berechnen Sie die Wahrscheinlichkeit, dass bei dreimaligem Ziehen mindestens zwei gelbe Spielbälle gezogen werden.
Die Bälle sind mit den Zahlen eins bis elf durchnummeriert. Serkan nimmt die restlichen Bälle aus dem Behälter und legt alle 11 Bälle vor sich in einer Reihe hin. Berechnen Sie die Anzahl aller möglichen verschiedenen Reihenfolgen, in der die Bälle gelegt werden könnten.