Aufgabengruppe II
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
Lösen Sie die folgenden Aufgaben.
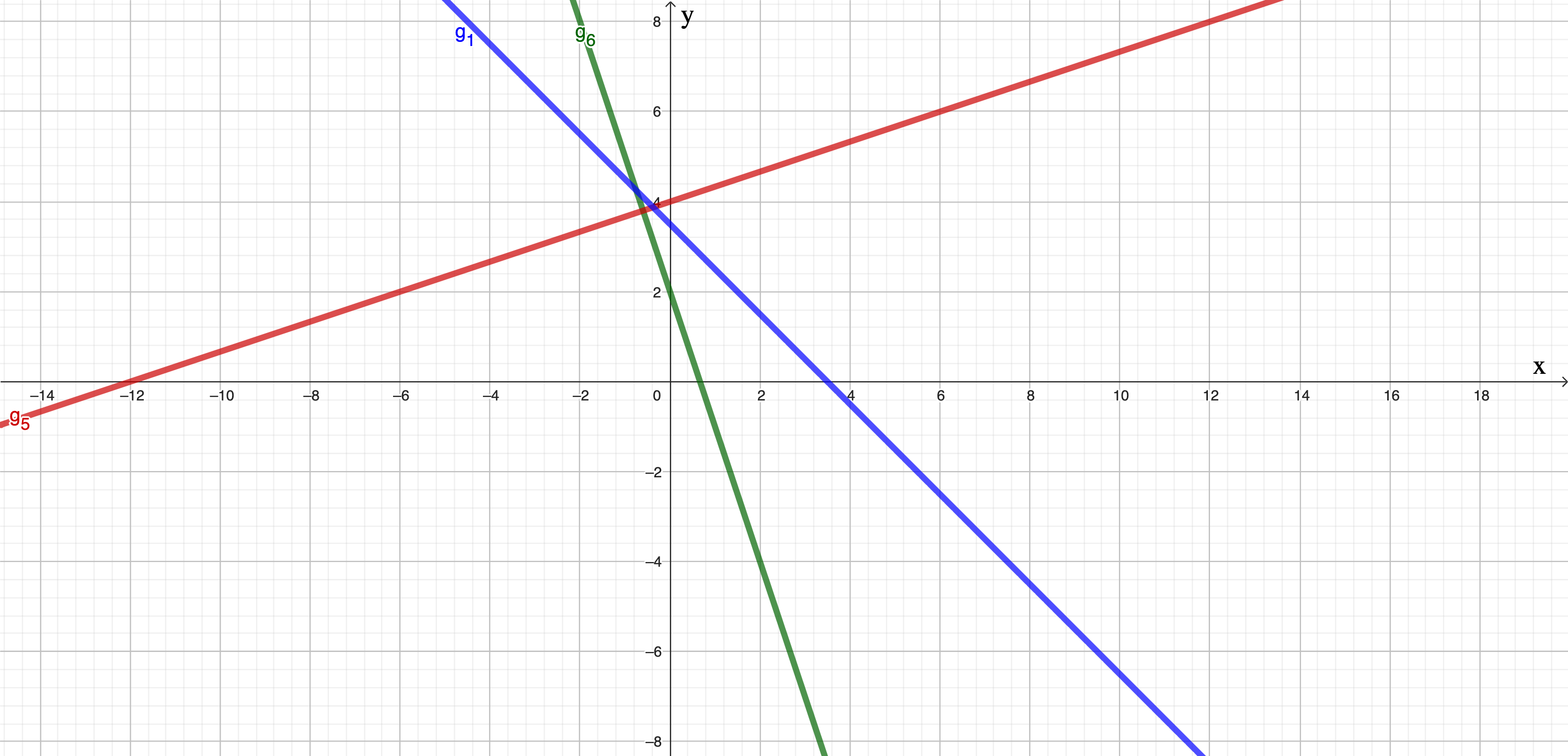
Die Gerade ist durch die Funktionsgleichung bestimmt. Berechnen Sie die Koordinaten des Schnittpunkts der Geraden mit der x-Achse und geben Sie an.
Die folgenden Wertepaare sind Punkte der Geraden :
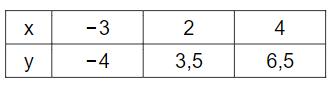
Ermitteln Sie die Funktionsgleichung von .
Die Gerade schneidet die Gerade im Punkt . Berechnen Sie die Koordinaten des Schnittpunkts und geben Sie diesen an.
Die Gerade wird zuerst an der x-Achse und dann an der y-Achse gespiegelt. Dadurch entsteht die Gerade . Geben Sie die Funktionsgleichung von an.
Die Gerade hat die Funktionsgleichung . Die Gerade steht senkrecht auf und verläuft durch den Punkt . Bestimmen Sie rechnerisch die Funktionsgleichung von .
Zeichnen Sie die Geraden , und in ein Koordinatensystem mit der Längeneinheit 1 cm.
- 2
Martina stellt Vogelfutter her. Für die Herstellung des Teigs verwendet sie einen Topf in Form eines Zylinders. Dieser hat im Inneren einen Durchmesser von 26 cm und eine Höhe von 28 cm. Die Teigmasse füllt den Topf bis 8 cm unter den Rand. Martina formt damit Kugeln mit einem Durchmesser von 5 cm, solange dies möglich ist. Aus der übrigen Teigmasse fertigt sie eine letzte, kleinere Kugel. Berechnen Sie den Durchmesser dieser kleineren Kugel.
- 3
In der folgenden Skizze gilt:
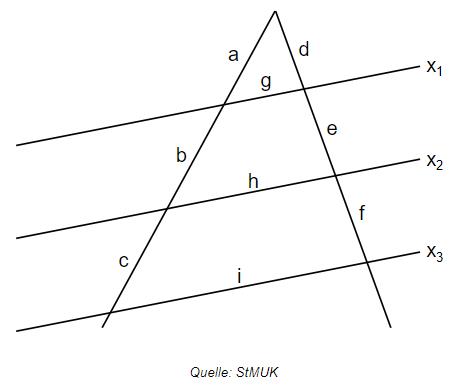
Hinweis: Skizze nicht maßstabsgetreu
Schreiben Sie die folgenden Aussagen auf Ihr Lösungsblatt und ersetzen Sie jeweils den Platzhalter so, dass die Beziehungen richtig wiedergegeben werden.
II.
III.
Folgende Streckenlängen sind gegeben: a = 4 cm; b = 6 cm; g = 2 cm. Berechnen Sie die Länge der Strecke h.
cm
- 4
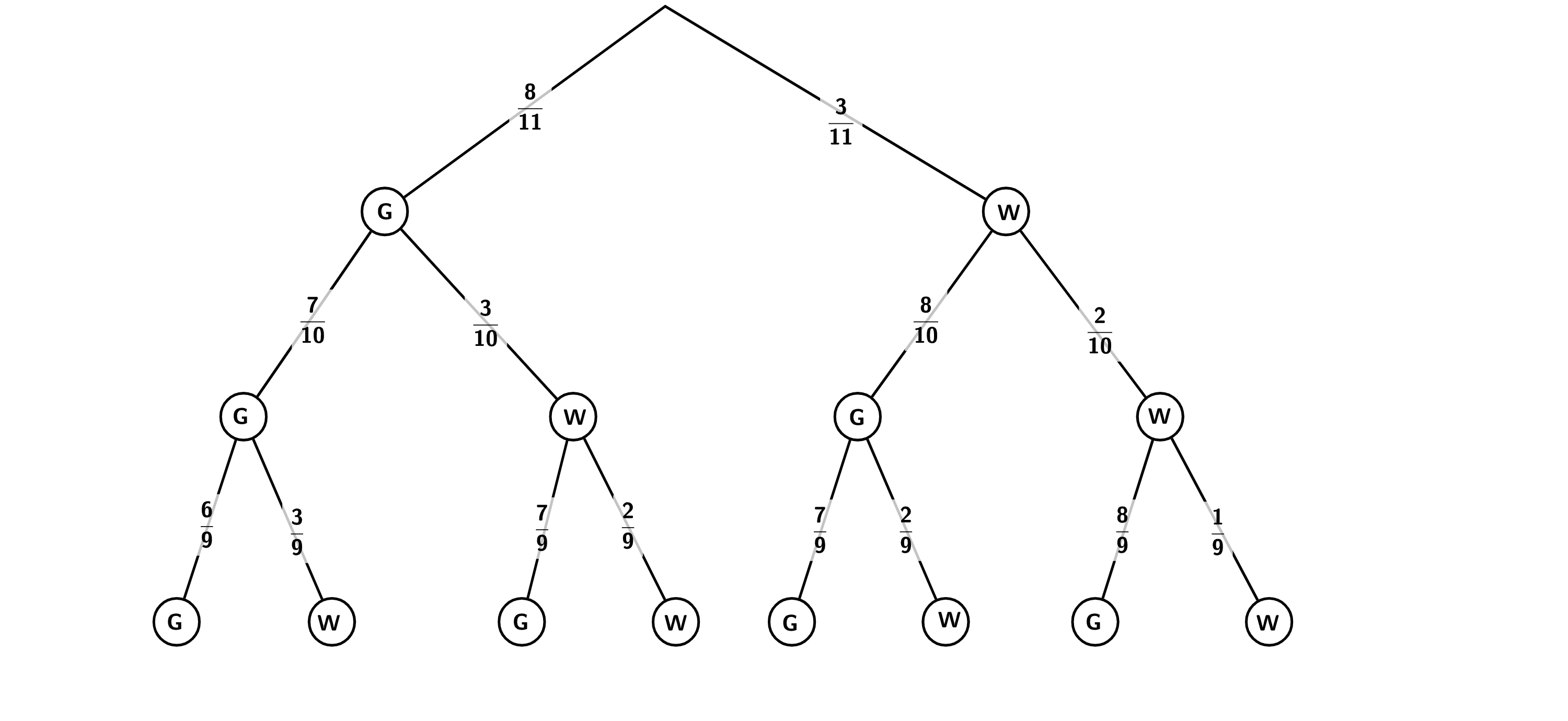
In einem Behälter befinden sich acht gelbe und drei weiße Spielbälle für ein Kickerturnier. Serkan nimmt nacheinander drei Spielbälle ohne Zurücklegen aus dem Behälter. Dies geschieht nach dem Zufallsprinzip.
Stellen Sie diesen Ablauf in einem Baumdiagramm dar und beschriften Sie die Äste mit den entsprechenden Wahrscheinlichkeiten.
Berechnen Sie die Wahrscheinlichkeit, dass bei dreimaligem Ziehen mindestens zwei gelbe Spielbälle gezogen werden.
Die Bälle sind mit den Zahlen eins bis elf durchnummeriert. Serkan nimmt die restlichen Bälle aus dem Behälter und legt alle 11 Bälle vor sich in einer Reihe hin. Berechnen Sie die Anzahl aller möglichen verschiedenen Reihenfolgen, in der die Bälle gelegt werden könnten.
- 5
Lösen Sie die folgenden Aufgaben.
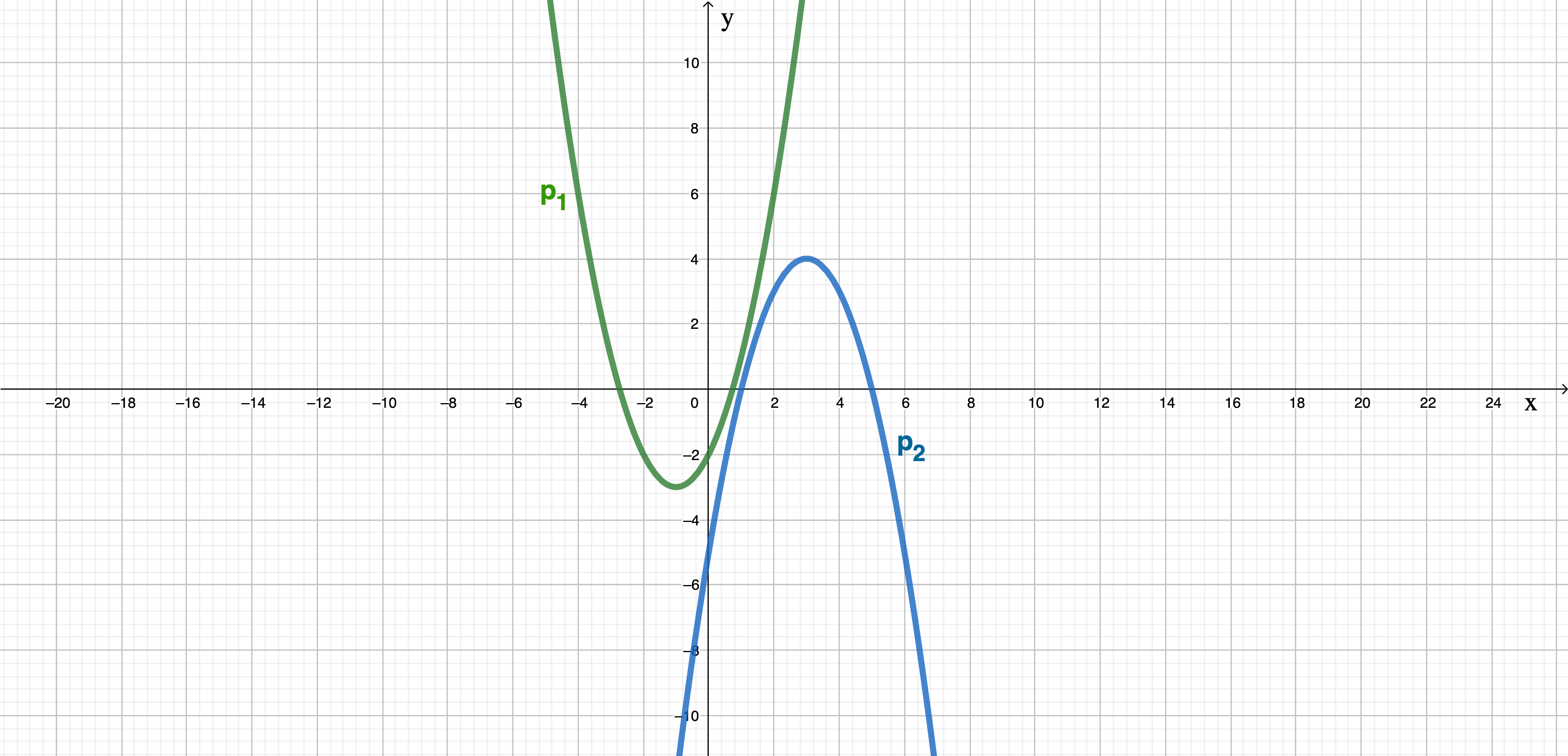
Die nach oben geöffnete Normalparabel verläuft durch die Punkte und . Geben Sie die Funktionsgleichung von in der Normalform an.
Die Normalparabel ist nach unten geöffnet und hat denScheitelpunkt ). Geben Sie die Funktionsgleichung von in der Normalform an
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der Längeneinheit 1 cm.
Der Punkt liegt auf der Normalparabel . Berechnen Sie die fehlende y-Koordinate.
Überprüfen Sie rechnerisch, ob der Punkt auf der Parabel liegt.
Bestimmen Sie durch Rechnung den Scheitelpunkt der Parabel .
Die Parabel schneidet die x-Achse in den Punkten und . Ermitteln Sie die x-Koordinaten von und rechnerisch.
Zeigen Sie rechnerisch, dass die Gerade keinen gemeinsamen Punkt mit der Parabel hat.
- 6
Lösen Sie folgende Aufgaben.
Ersetzen Sie den Platzhalter durch einen Term so, dass eine wahre Aussage entsteht. Dabei sind und beliebige, positive, reele Zahlen. Schreiben Sie die korrekte Gleichung auf Ihr Lösungsblatt.
Ersetzen Sie die Platzhalter ♦ (Rechenzeichen) und (Terme) in der folgenden Gleichung so, dass eine korrekte Anwendung einer binomischen Formel entsteht.Schreiben Sie diese Gleichung vollständig auf Ihr Lösungsblatt.
- 7
Die folgende Skizze zeigt die Fläche einer Werbetafel für eine Surfschule. Es gilt:
; ;
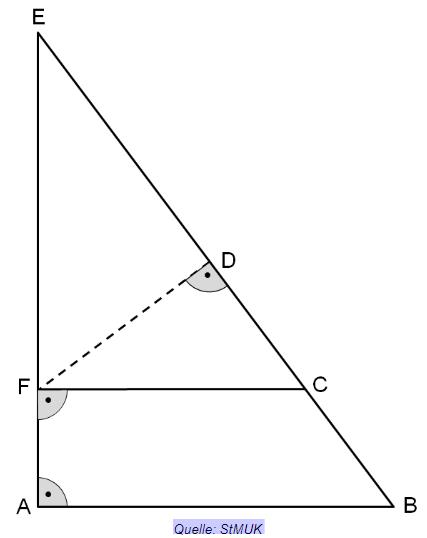
Hinweis: Skizze nicht maßstabsgetreu
Das Trapez ABCF der Werbetafel soll rot lackiert werden. Berechnen Sie den Flächeninhalt dieses Trapezes.
Der Umfang der Tafel soll entlang des Dreiecks ABE mit einem speziellen LED–Lichtschlauch beleuchtet werden. Diesen kann man nur bis zu einem Winkel von 25° biegen, damit er nicht bricht. Überprüfen Sie, ob der Lichtschlauch für dieses Dreieck geeignet ist.
- 8
Gegeben ist folgende Gleichung:
Geben Sie die Definitionsmenge an, lösen Sie die Gleichung nach x auf und bestimmen Sie die Lösungsmenge.
- 9
Die Bevölkerungszahl in deutschen Städten hat sich in den letzten Jahren verändert.
Am 1. Januar 2010 wohnten in einer Stadt 460725 Einwohner. Diese Einwohnerzahl stieg in neun Jahren um insgesamt 30800. Berechnen Sie das durchschnittliche jährliche Bevölkerungswachstum dieser Stadt in Prozent.
In einer Großstadt betrug am 1. Januar 2019 die Einwohnerzahl 1847253. Bestimmen Sie rechnerisch den Zeitraum in Jahren, in dem diese Großstadt bei einem durchschnittlichen jährlichen Wachstum von 0,38 % die Grenze von zwei Millionen Einwohnern überschreiten würde.
JahreIn anderen Städten sinken die Einwohnerzahlen. Berechnen Sie die Anzahl der Einwohner einer Stadt nach zehn Jahren, wenn diese momentan 246334 Einwohner zählt und man von einem jährlichen durchschnittlichen Rückgang von 1,01 % ausgeht.
EinwohnerIn vielen ländlichen Gebieten sinken die Einwohnerzahlen noch stärker. Am 1. Januar 2021 hatte eine kleine Gemeinde 2510 Einwohner. Seit dem 1. Januar 2000 nahm die Einwohnerzahl durchschnittlich um jährlich 2,8 % ab. Berechnen Sie die Anzahl der Einwohner am 1. Januar 2000.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?