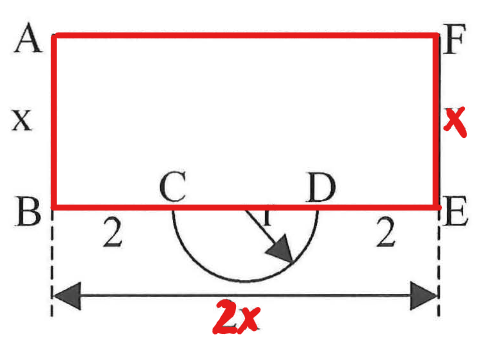
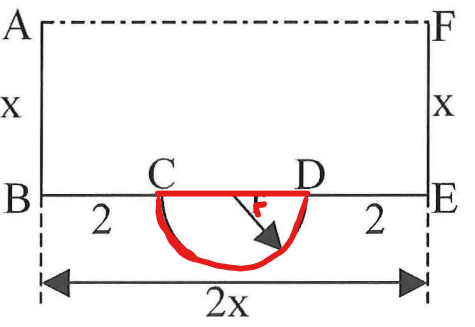
Der Querschnitt eines Abflusskanals ist begrenzt durch ein Rechteck und einen Halbkreis mit Radius r. Alle Angaben sind in Meter. Auf Einheiten wird in der Rechnung verzichtet.
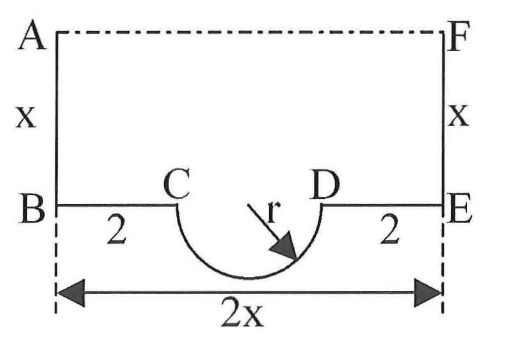
Zeigen Sie, dass sich die Maßzahl A(x) der Querschnittsfläche des Kanals in Abhängigkeit von x durch darstellen lässt. (5 BE)
Die Strecken [AB], [BC], [DE] und [EF] besitzen in der Summe höchstens eine Länge von 12 m.
Weisen Sie nach, dass dann für die sinnvolle maximale Definitionsmenge der Funktion gilt: . (3 BE)
Bestimmen Sie x so, dass die zugehörige Querschnittsfläche maximalen Inhalt annimmt. (4 BE)
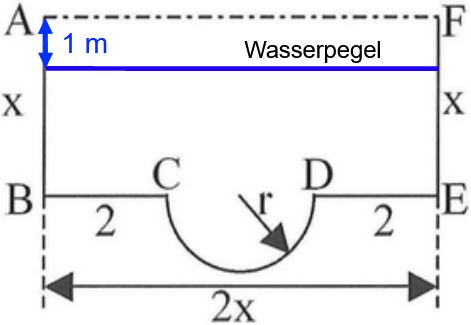
Nun sei Der Kanal ist bis 1 m unter der Oberkante gefüllt. Berechnen Sie, wie viel Prozent der Querschnittsfläche des Kanals ausgelastet sind. (3 BE)