Aufgabengruppe A1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Gegeben ist die reelle Funktion mit dem Definitionsbereich .
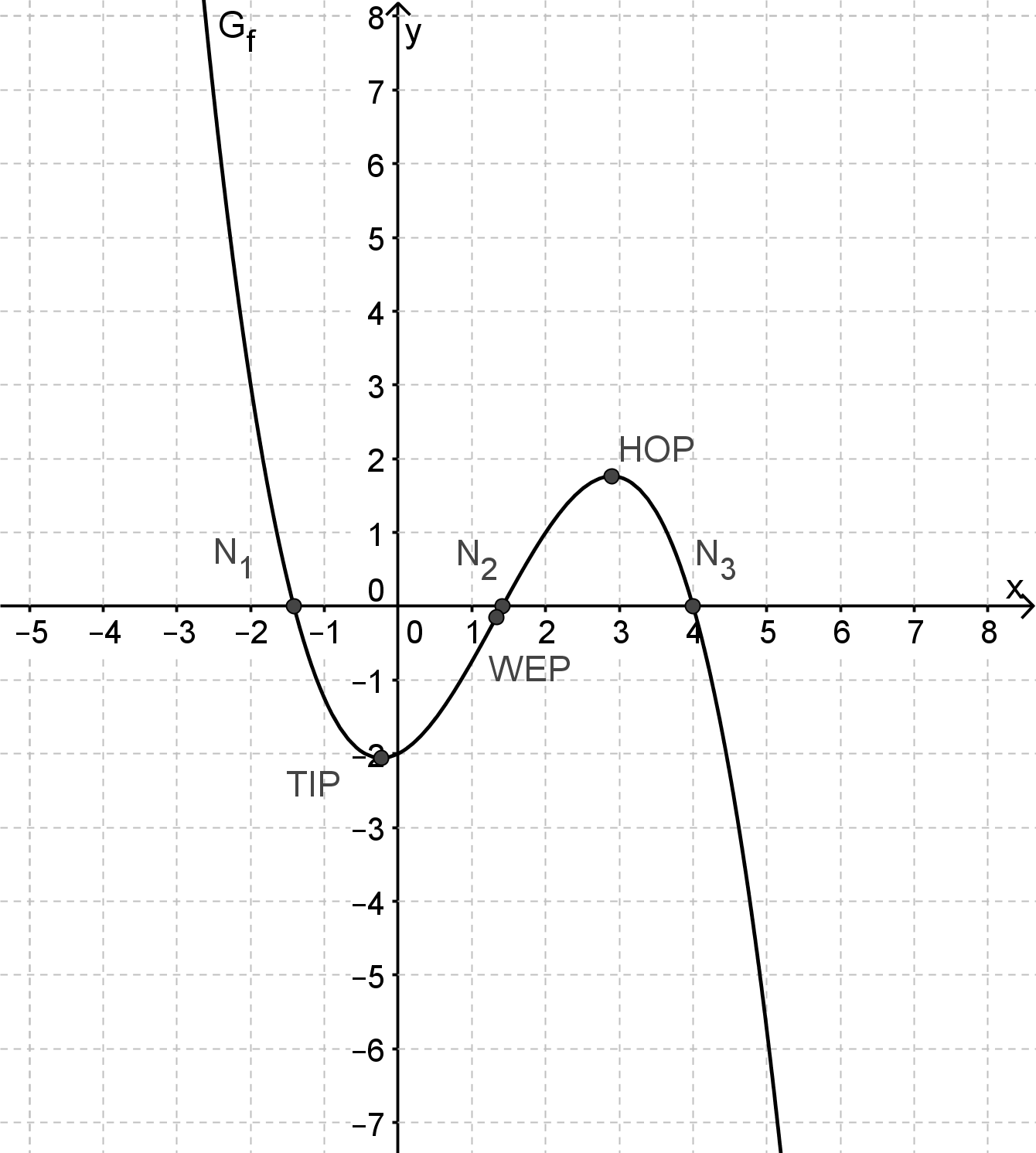
Bestimmen Sie sämtliche Nullstellen der Funktion f und deren Vielfachheit. Begründen Sie dann ohne weitere Rechnung, dass in den Intervallen sowie jeweils eine Extremstelle liegt. Geben Sie auch deren Art an. (7 BE)
Berechnen Sie Art und Koordinaten der Extrempunkte des Graphen . Runden Sie auf zwei Stellen nach dem Komma. (5 BE)
Ermitteln Sie die maximalen Intervalle, in denen der Graph rechts- bzw. linksgekrümmt ist, sowie die Koordinaten des Wendepunkts. (4 BE)
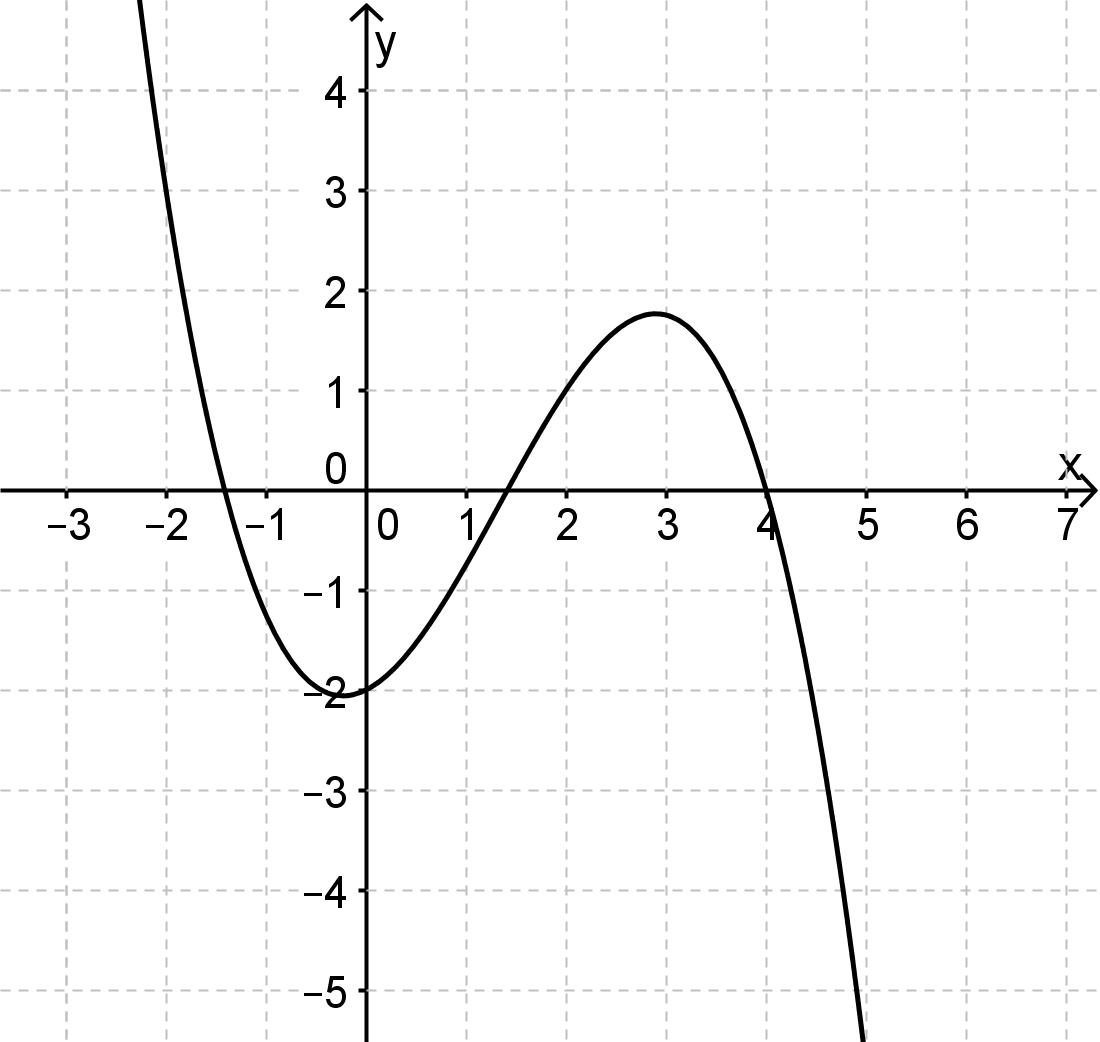
Zeichnen Sie den Graphen im Bereich auch unter Verwendung der vorliegenden Ergebnisse, in ein kartesisches Koordinatensystem (4 BE)
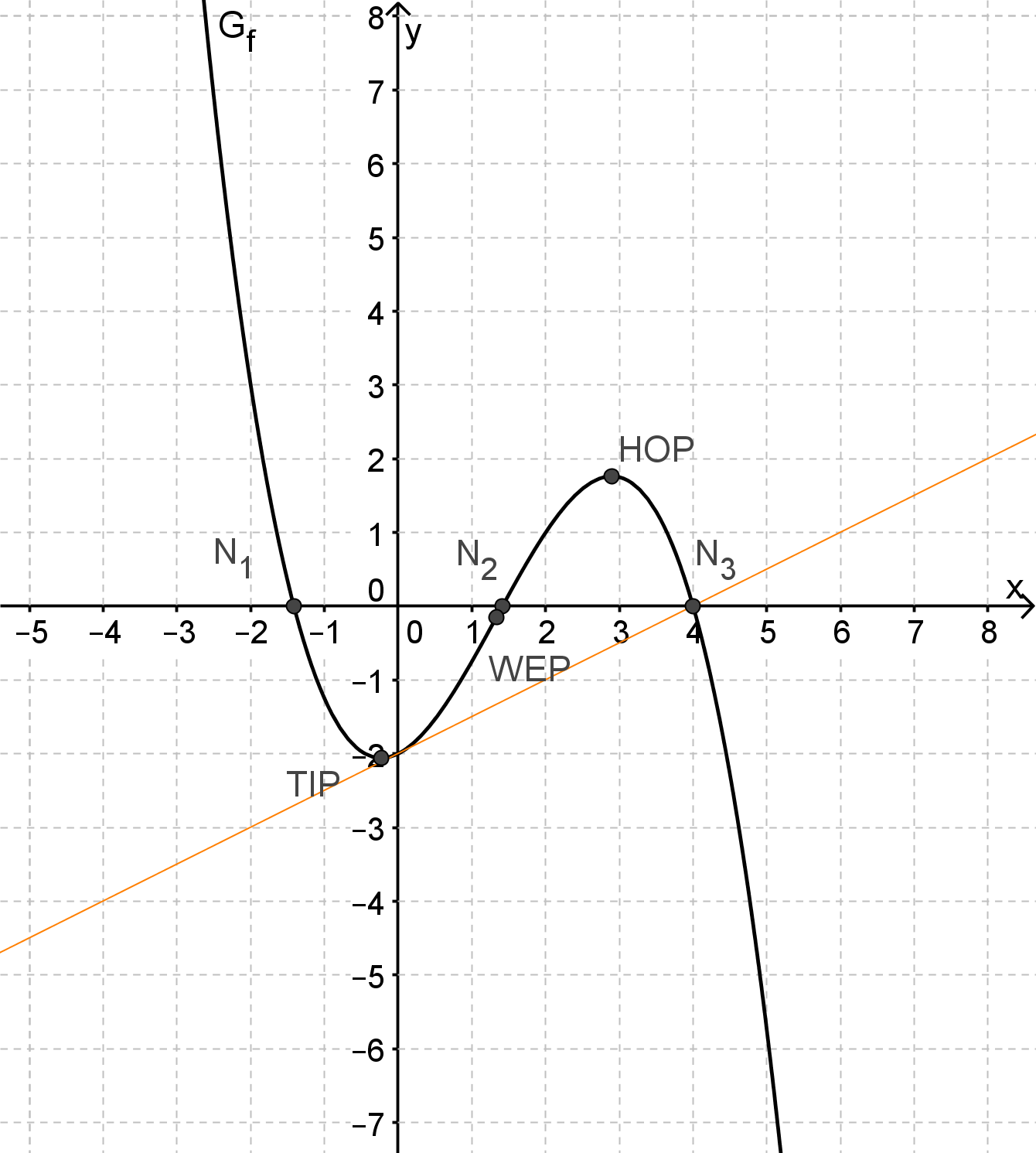
Die Gerade enthält die Schnittpunkte des Graphen mit der y-Achse und mit der x-Achse bei . Zeigen Sie, dass die Gerade Tangente an ist und zeichnen Sie in das vorhandene Koordinatensystem ein. (4 BE)
Die Graphen und schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl seines Flächeninhalts. (4 BE)
Gegeben ist zusätzlich die Funktion p mit und es gilt: .
Bestimmen Sie die Nullstellen der Funktionen mit deren Vielfachheit und erläutern Sie die geometrische Bedeutung dieser Stellen für den Graphen der beiden Funktionen. (4 BE)
- 2
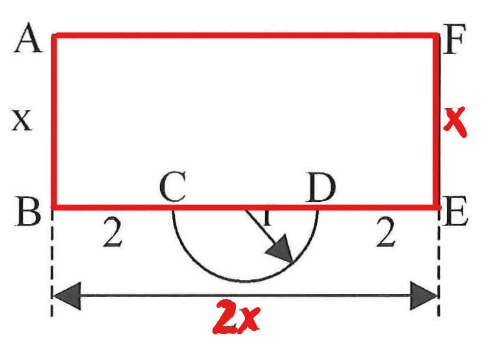
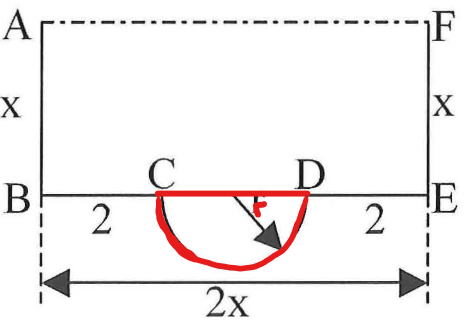
Der Querschnitt eines Abflusskanals ist begrenzt durch ein Rechteck und einen Halbkreis mit Radius r. Alle Angaben sind in Meter. Auf Einheiten wird in der Rechnung verzichtet.
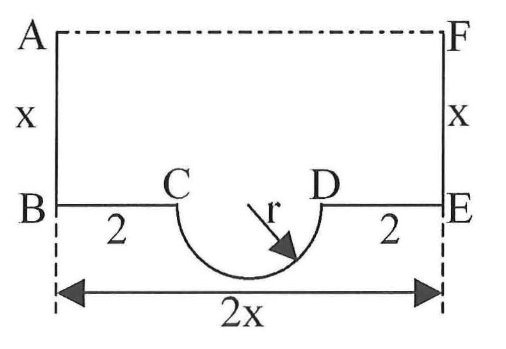
Zeigen Sie, dass sich die Maßzahl A(x) der Querschnittsfläche des Kanals in Abhängigkeit von x durch darstellen lässt. (5 BE)
Die Strecken [AB], [BC], [DE] und [EF] besitzen in der Summe höchstens eine Länge von 12 m.
Weisen Sie nach, dass dann für die sinnvolle maximale Definitionsmenge der Funktion gilt: . (3 BE)
Bestimmen Sie x so, dass die zugehörige Querschnittsfläche maximalen Inhalt annimmt. (4 BE)
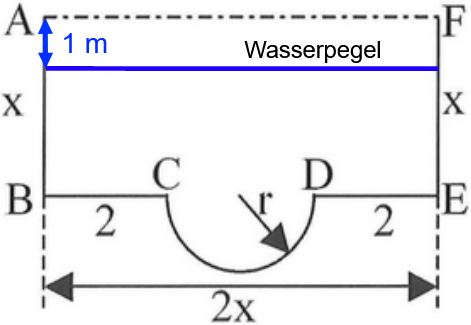
Nun sei Der Kanal ist bis 1 m unter der Oberkante gefüllt. Berechnen Sie, wie viel Prozent der Querschnittsfläche des Kanals ausgelastet sind. (3 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?