Teil B - lernen mit Serlo!

Aufgabe B2

Gegeben sind die Geraden $g$ : $y = 0,25 x - 3$ und $h$ : ⁣ $y = 0,6 x$ $(𝔾 = ℝ \times ℝ)$ .

Punkte $B_{n} (x | 0,25 x - 3)$ auf der Geraden $g$ bilden für $x > 1,57$ zusammen mit dem Punkt

$A (0 | 0)$ und Punkten $C_{n}$ und $D_{n}$ Rauten $A B_{n} C_{n} D_{n}$ , wobei die Gerade $h = A C_{n}$ eine der Symmetrieachsen der Rauten ist.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

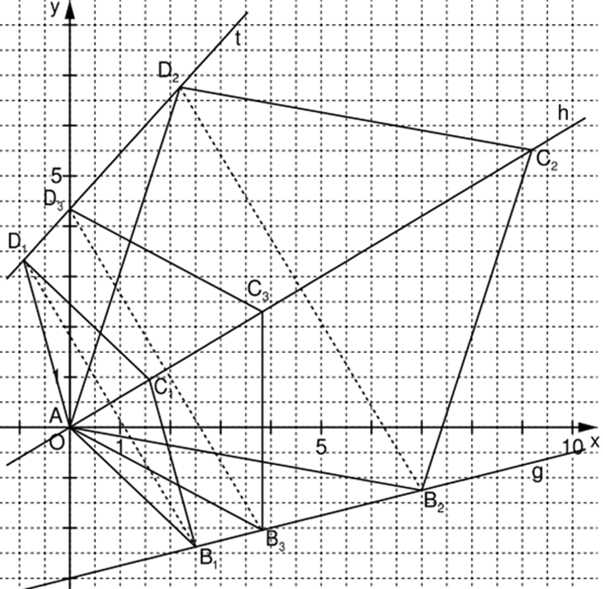
Zeichnen Sie die Geraden $g$ und $h$ sowie die Rauten $A B_{1} C_{1} D_{1}$ für $x = 2,5$ und $A B_{2} C_{2} D_{2}$ für $x = 7$ in ein Koordinatensystem. (3 BE)
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 1 \leq x \leq 10$ ; $- 4 \leq y \leq 8$

geg.: Geraden: $g : y = 0,25 x - 3; h : y = 0,6 x; 𝔾 = ℝ 𝕩 ℝ$
Rauten: $A B_{n} C_{n} D_{n} m i t A (0 | 0), 𝐁_{𝐧} (𝐱 | 𝟎,𝟐𝟓 𝐱 - 𝟑), C_{n}, D_{n}$
wobei $h = A C_{n}$ Symmetrieachse der Rauten ist
Zeichenbereich: $- 1 \leq x \leq 10$ und $- 4 \leq y \leq 8$ ; $L E = 1 c m$
ges.: Geraden $g$ und $h$ ; Raute $A B_{1} C_{1} D_{1}$ für $x = 2,5$ und Raute $A B_{2} C_{2} D_{2}$ für $x = 7$
Anleitung zum Einzeichnen
1. $A (0 | 0$ ) einzeichnen
2. für $g$ und $h$ jeweils $2$ Punkte berechnen und Geraden ins Koordinatensystem einzeichnen
3. $B_{1}$ und $B_{2}$ für $x = 2,5$ und $x = 7$ auf $g$ eintragen; dann $C_{1}$ und $D_{1}$ sowie $C_{2}$ und $D_{2}$ zu Rauten ergänzen
Geraden und Rauten im Koordinatensystem
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeichne die Geraden $g$ und $h$ sowie Rauten ins Koordinatensystem ein.
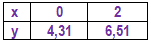
Ermitteln Sie rechnerisch die Koordinaten der Punkte $D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ . (3 BE)
$[$ Ergebnis: $D_{n} (0,69 x - 2,64 | 0,76 x + 1,41)]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung mit Matrizen
geg.: Punkte $B_{n} (x | 0,25 x - 3)$ , Gerade $h : y = 0,6 x$
ges.: Abbildung der Punkte $B_{n}$ via h nach $D_{n}$
Berechnung Winkel $φ$ zwischen x-Achse und Spiegelachse
$h : y = 0,6 x$ $\Rightarrow \tan φ = 0,6 \Rightarrow 𝛗 = 𝟑𝟎,𝟗𝟔 °$
Spiegelungsmatrix an einer Ursprungsgeraden mit dem Winkel $α$ zur positiven $x -$ Achse
$S g = (\begin{array}{cc} \cos 2 α & \sin 2 α \\ \sin 2 α & - \cos 2 α \end{array})$
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos (2 α) & \sin (2 α) \\ \sin (2 α) & - \cos (2 α) \end{array}) ⊙ (\begin{array}{c} x_{B} \\ y_{B} \end{array})$
Werte für $x_{B}$ und $y_{B}$ einsetzen:
$\Rightarrow (\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos (2 φ) & \sin (2 φ) \\ \sin (2 φ) & - \cos (2 φ) \end{array}) ⊙ (\begin{array}{c} x \\ 0,25 x - 3 \end{array})$
Wert für $φ$ einsetzen und Sinus/Kosinus-Werte berechnen:
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos (2 \cdot 30,96 °) & \sin (2 \cdot 30,96 °) \\ \sin (2 \cdot 30,96 °) & - \cos (2 \cdot 30,96 °) \end{array}) ⊙ (\begin{array}{c} x \\ 0,25 x - 3 \end{array})$
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos (61,92 °) & \sin (61,92 °) \\ \sin (61,92 °) & - \cos (61,92 °) \end{array}) ⊙ (\begin{array}{c} x \\ 0,25 x - 3 \end{array})$
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} 0,47 & 0,88 \\ 0,88 & - 0,47 \end{array}) ⊙ (\begin{array}{c} x \\ 0,25 x - 3 \end{array})$
Multiplikation der Abbildungsmatrix mit einem Vektor
$Multiplikationsregel: (\begin{array}{c} x^{^{'}} \\ y^{^{'}} \end{array}) = (\begin{array}{cc} a & b \\ c & d \end{array}) ⊙ (\begin{array}{c} x \\ y \end{array}) = (\begin{array}{c} a \cdot x + b \cdot y \\ c \cdot x + d \cdot y \end{array})$
$\Rightarrow (\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{c} 0,47 \cdot x + 0,88 \cdot (0,25 x - 3) \\ 0,88 \cdot x + (- 0,47) \cdot (0,25 x - 3) \end{array})$
$\Rightarrow (\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{c} 0,47 x + 0,22 x - 2,64 \\ 0,88 x - 0,1175 x + 1,41 \end{array})$
$\Rightarrow (\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{c} 0,69 x - 2,64 \\ 0,76 x + 1,41 \end{array})$
$\Rightarrow$ Koordinaten der Punkte $D_{n} (x) : 𝐃_{𝐧} (𝟎,𝟔𝟗 𝐱 - 𝟐,𝟔𝟒 | 𝟎,𝟕𝟔 𝐱 + 𝟏,𝟒𝟏)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Winkel $φ$ zwischen $x -$ Achse und Spiegelachse.
Berechne die Abbildung der Punkte $B_{n}$ via Spiegelachse $h$ nach $D_{n}$ .
Überprüfen Sie rechnerisch, ob die Raute $A B_{2} C_{2} D_{2}$ ein Quadrat ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Eigenschaften Raute und Quadrat
geg.: gleichseitiges Parallelogramm, achsensymmetrisch und punktsymmetrisch
ges.: Ist $A B_{2} C_{2} D_{2}$ ein Quadrat ?
Berechnung
Die Raute wäre dann ein Quadrat, wenn zwei Seiten senkrecht zueinander stehen.
Dies ist der Fall, wenn das Skalarprodukt $\vec{𝐀 𝐁_{𝟐}} ⊙ \vec{𝐀 𝐃_{𝟐}} = 𝟎$ ist.
Mit $A (0 | 0)$ und $B_{2} (x | 0,25 \cdot x - 3)$ für $x = 7$ $\Rightarrow$
$\vec{𝐀 𝐁_{𝟐}} = (\begin{array}{c} x - 0 \\ (0,25 x - 3) \end{array}) = (\begin{array}{c} 7 - 0 \\ 0,25 \cdot 7 - 3 \end{array}) = (\begin{array}{c} 𝟕 \\ - 𝟏,𝟐𝟓 \end{array})$
Mit $A (0 | 0)$ und $D_{2} (0,69 x - 2,64 | 0,76 x + 1,41)$ aus Aufgabe B 2.b für $x = 7$ $\Rightarrow$
$\vec{𝐀 𝐃_{𝟐}} = (\begin{array}{c} 0,69 \cdot x - 2,64 \\ 0,76 \cdot x + 1,41 \end{array}) = (\begin{array}{c} 0,69 \cdot 7 - 2,64 \\ 0,76 \cdot 7 + 1,41 \end{array}) = (\begin{array}{c} 𝟐,𝟏𝟗 \\ 𝟔,𝟕𝟑 \end{array})$
Ist das Skalarprodukt $\vec{𝐀 𝐁_{𝟐}} ⊙ \vec{𝐀 𝐃_{𝟐}} = 𝟎$ ?
$(\begin{array}{c} 7 \\ - 1,25 \end{array}) ⊙ (\begin{array}{c} 2,19 \\ 6,73 \end{array}) = 7 \cdot 2,19 + (- 1,25) \cdot 6,73 = 15,33 - 8,4125 = 𝟔,𝟗𝟏𝟕𝟓 \neq 𝟎$
$\Rightarrow$ Die Raute $𝐀 𝐁_{𝟐} 𝐂_{𝟐} 𝐃_{𝟐}$ ist kein Quadrat!
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überprüfe, ob die Seiten im rechten Winkel zueinander stehen.
Berechne dazu die Skalarprodukte.
Bestimmen Sie die Gleichung des Trägergraphen $t$ der Punkte $D_{n}$ .
Zeichnen Sie sodann den Trägergraphen $t$ in das Koordinatensystem zur Teilaufgabe (a) ein. (3 BE)

geg.: $D_{n} (0,69 x - 2,64 | 0,76 x + 1,41)$
ges.: Gleichung für Trägergraph $t$
Aus $D_{n} (0,69 x - 2,64 | 0,76 x + 1,41)$ Gleichungssystem aufstellen:
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{c} 0,69 x - 2,64 \\ 0,76 x + 1,41 \end{array})$
I. $𝐱_{𝐃_{𝐧}} = 𝟎,𝟔𝟗 𝐱 - 𝟐,𝟔𝟒$
II. $𝐲_{𝐃_{𝐧}} = 𝟎,𝟕𝟔 𝐱 + 𝟏,𝟒𝟏$ $𝔾 = ℝ \times ℝ; x \in ℝ; x > 1,57$
$x_{D_{n}} + 2,64 = 0,69 x$ nach $x$ auflösen:
$\Rightarrow x = \frac{(x_{D_{n}} + 2,64)}{0,69} \Rightarrow x = \frac{x_{D_{n}}}{0,69} + \frac{2,64}{0,69}; \Rightarrow 𝐱 = 𝟏,𝟒𝟓 𝐱_{𝐃_{𝐧}} + 𝟑,𝟖𝟐$
$x$ in $y_{D_{n}}$ einsetzen:
$y_{D_{n}} = 0,76 \cdot (1,45 x_{D_{n}} + 3,82) + 1,41$
$y_{D_{n}} = 1,10 x_{D_{n}} + 2,90 + 1,41$
$𝐲_{𝐃_{𝐧}} = 𝟏,𝟏𝟎 𝐱_{𝐃_{𝐧}} + 𝟒,𝟑𝟏 𝔾 = ℝ \times ℝ$
$\Rightarrow$ Trägergraph $𝐭 : 𝐲 = 𝟏,𝟏𝟎 𝐱 + 𝟒,𝟑𝟏$
Einzeichnen des Trägergraphen $t$ durch die Punkte $D_{n}$ :
Punkte auf $t$ : Graph siehe Aufgabe 2.a
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für die Punkte $D_{n}$ gilt $D_{n} (x^{'} | Trägergraphgleichung)$ :
1. Gleichungssystem für $I . x_{D} = \dots$ und $I I . y_{D} = \dots$ aufstellen
2. $I .$ nach $x^{'}$ auflösen und
3. in $I I .$ einsetzen.
4. Trägergraph einzeichnen
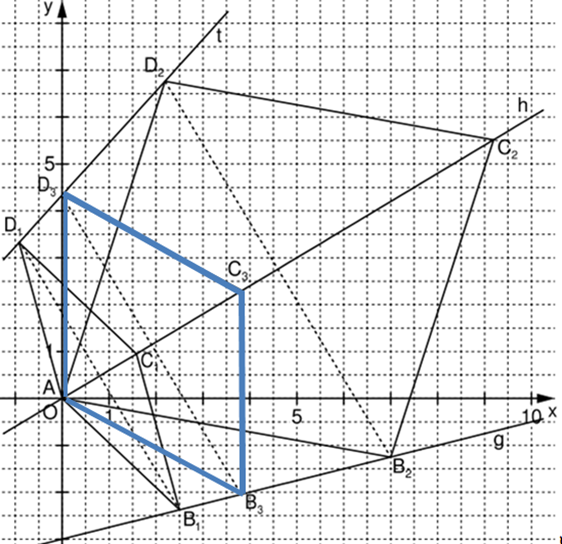
Der Punkt $D_{3}$ der Raute $A B_{3} C_{3} D_{3}$ liegt auf der y-Achse.
Zeichnen Sie die Raute $A B_{3} C_{3} D_{3}$ in das Koordinatensystem zur Teilaufgabe (a) ein.
Berechnen Sie sodann die Koordinaten des Punktes $C_{3}$ sowie den Flächeninhalt der Raute $A B_{3} C_{3} D_{3}$ . (5 BE)
$[$ Teilergebnis: $x_{C_{3}} = 3,83]$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächen der Raute
geg.: Träger $h$ des Punktes $C_{3}$
ges.: Raute im Koordinatensystem, Punkt $C_{3}$ , Fläche $A B_{3} C_{3} D_{3}$
Einzeichnen der Raute $A B_{3} C_{3} D_{3}$ siehe Bild
Berechnung der Koordinaten von $C_{3}$ :
Koordinaten von $D_{n}$ in Abhängigkeit der Abszisse $x : D_{n} (0,69 x - 2,64 | 0,76 x + 1,41)$ , siehe Aufgabe B 2.b
$\Rightarrow 0,69 x - 2,64 = 0 x \in ℝ; x > 1,57$
$\Rightarrow 0,69 x = 2,64 x = \frac{2,64}{0,69} = 3,826 \approx 3,83 \Rightarrow L = {3,83}$
$x$ in Gleichung für $h$ einsetzen:
Flächeninhalt der Raute $A B_{3} C_{3} D_{3}$ ist ein gleichseitiges Parallelogramm,
$\Rightarrow A_{A B_{3} C_{3} D_{3}} : A = a \cdot h_{a}$
Berechnung $𝐚$ :
Der Trägergraph $𝐲 = 𝟏,𝟏𝟎 𝐱 + 𝟒,𝟑𝟏$ (siehe Aufgabe (d)) ist für $x = 0$ :
$y = 1,10 x + 4,31 = 1,10 \cdot 0 + 4,31 = 4,31$
$\Rightarrow$ Strecke $[𝐀 𝐃_{𝟑}] = 𝐚 = 𝟒,𝟑𝟏$ LE
Berechnung $𝐡_{𝐚}$ $≙$ Abstand $d$ zwischen Punkt $C_{3}$ und Strecke $A D_{3}$ ,
daher ist $𝐝 (𝐂_{𝟑}; 𝐀 𝐃_{𝟑}) = 𝟑,𝟖𝟑$ LE
Mit $𝐚 ≙ [𝐀 𝐃_{𝟑}]$ und $𝐡_{𝐚} ≙ 𝐝 (𝐂_{𝟑}; 𝐀 𝐃_{𝟑})$ $\Rightarrow$
Fläche $𝐀_{𝐀 𝐁_{𝟑} 𝐂_{𝟑} 𝐃_{𝟑}} = A D_{3} \cdot d (C_{3}; A D_{3}) = 4,31 \cdot 3,83 = 𝟏𝟔,𝟓𝟓 𝐅 𝐄$
Raute $A B_{3} C_{3} D_{3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeichne die Raute $A B_{3} C_{3} D_{3}$ .
Berechne die Koordinate $C_{3}$
Berechne die Fläche der Raute $A B_{3} C_{3} D_{3}$ .

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Aufgabe B2

Anleitung zum Einzeichnen

Hast du eine Frage oder Feedback?

Berechnung Winkel φ zwischen x-Achse und Spiegelachse

Spiegelungsmatrix an einer Ursprungsgeraden mit dem Winkel α zur positiven x−Achse

Multiplikation der Abbildungsmatrix mit einem Vektor

Hast du eine Frage oder Feedback?

Berechnung

Hast du eine Frage oder Feedback?

Aus Dn(0,69x−2,64|0,76x+1,41) Gleichungssystem aufstellen:

xDn+2,64=0,69x nach x auflösen:

x in yDn einsetzen:

Einzeichnen des Trägergraphen t durch die Punkte Dn:

Hast du eine Frage oder Feedback?

Einzeichnen der Raute AB3C3D3 siehe Bild

Berechnung der Koordinaten von C3:

Flächeninhalt der Raute AB3C3D3 ist ein gleichseitiges Parallelogramm,

Hast du eine Frage oder Feedback?

Berechnung Winkel $φ$ zwischen x-Achse und Spiegelachse

Spiegelungsmatrix an einer Ursprungsgeraden mit dem Winkel $α$ zur positiven $x -$ Achse

Aus $D_{n} (0,69 x - 2,64 | 0,76 x + 1,41)$ Gleichungssystem aufstellen:

$x_{D_{n}} + 2,64 = 0,69 x$ nach $x$ auflösen:

$x$ in $y_{D_{n}}$ einsetzen:

Einzeichnen des Trägergraphen $t$ durch die Punkte $D_{n}$ :

Einzeichnen der Raute $A B_{3} C_{3} D_{3}$ siehe Bild

Berechnung der Koordinaten von $C_{3}$ :

Flächeninhalt der Raute $A B_{3} C_{3} D_{3}$ ist ein gleichseitiges Parallelogramm,