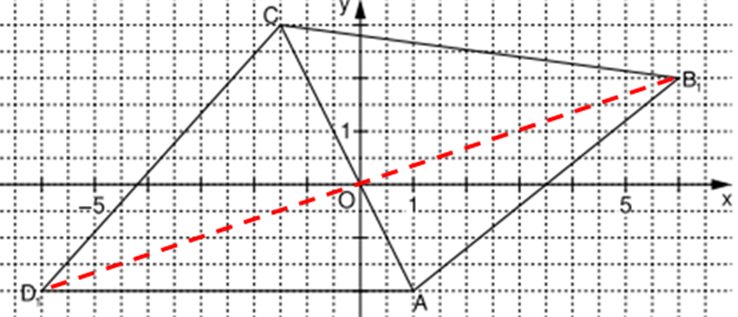
Aufgabe A3
Die Punkte und legen für zusammen mit
Pfeilen Dreiecke fest.
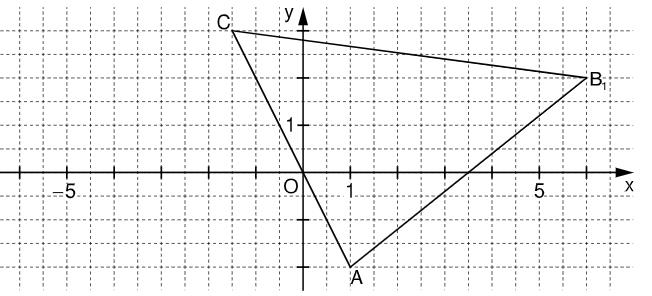
Im Koordinatensystem ist das Dreieck für eingezeichnet.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Die Punkte werden durch Punktspiegelung an auf Punkte abgebildet. Dadurch entstehen Vierecke .
Ergänzen Sie im Koordinatensystem zu A3.0 das Dreieck zum Viereck .
Zeigen Sie sodann rechnerisch, dass für die Koordinaten der Punkte in Abhängigkeit von gilt:
(3 P)
Begründen Sie, weshalb es unter den Vierecken kein Parallelogramm gibt. (2 P)