Aufgabe A2
Gegeben ist das Dreieck mit den Seitenlängen , und .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
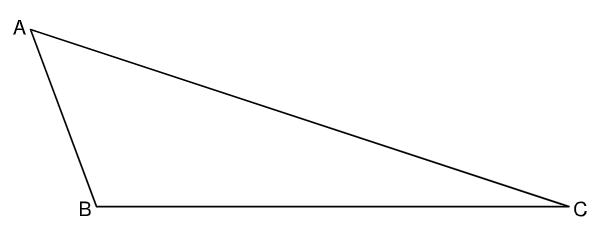
Berechnen Sie das Maß des Winkels . (2 P)
Ergebnis:
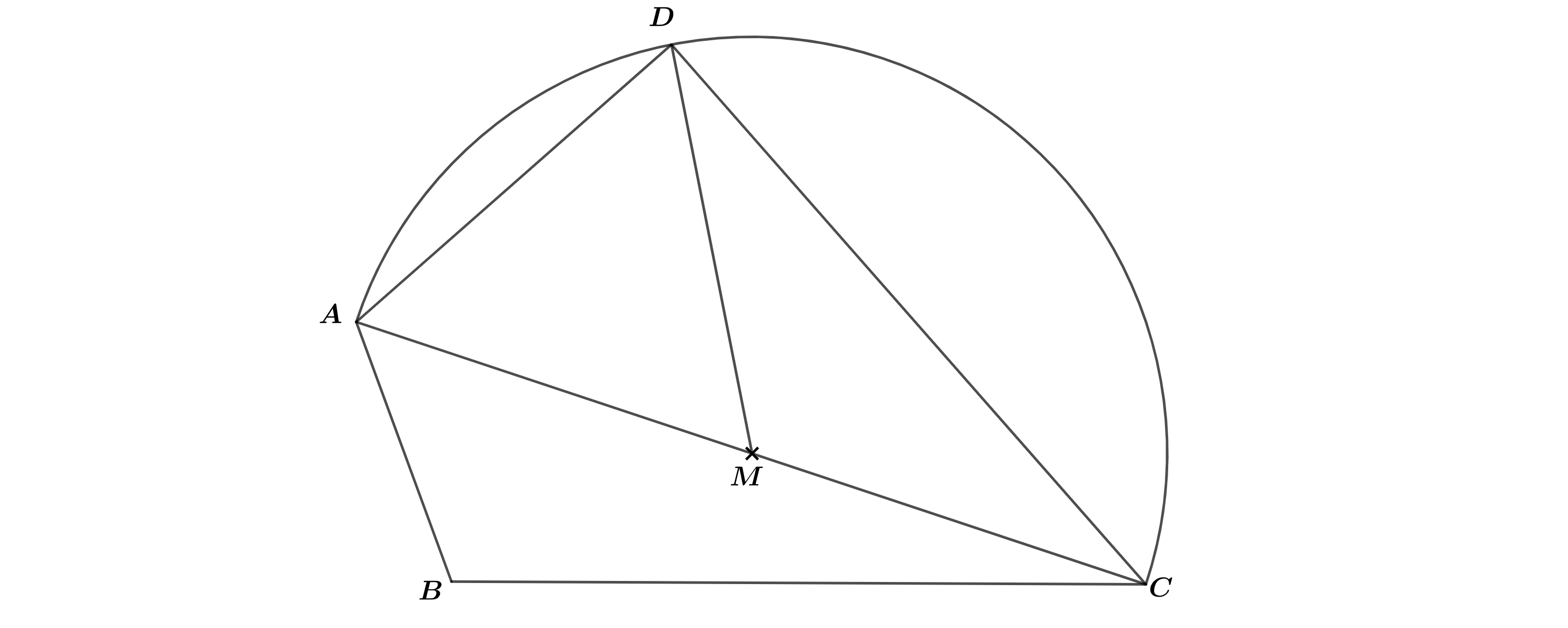
Der Punkt ist der Mittelpunkt der Strecke . Auf dem Kreisbogen mit dem Mittelpunkt liegt der Punkt mit .
Zeichnen Sie den Kreisbogen , das Dreieck und die Strecke in die Zeichnung zu 2) ein. (2 P)
Begründen Sie, weshalb der Winkel das Maß und der Winkel das Maß hat. (2 P)
Berechnen Sie den Flächeninhalt der Figur, die durch den Kreisbogen sowie die Strecken , und begrenzt wird. (3 P)