Aufgabe A3
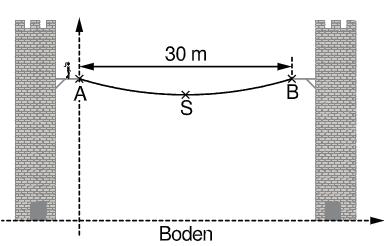
An zwei Türmen sind auf einer Höhe von jeweils über dem Boden Plattformen angebracht. Zwischen den beiden voneinander entfernten Plattformen ist eine Brücke gespannt. Der Verlauf der Brücke zwischen den Punkten und kann näherungsweise durch eine Parabel beschrieben werden. Diese hat eine Gleichung der Form
, ;
und den Scheitelpunkt . Dabei entspricht der horizontal gemessenen Entfernung vom Punkt und der Höhe über dem Boden.
Zeigen Sie rechnerisch, dass für die Gleichung der Parabel gilt:
, . (3 P)
Eine Person überquert die Brücke von nach . Sie geht bereits wieder aufwärts. Bei einer Höhe von Metern über dem Boden bleibt sie stehen. Diese Position entspricht dem Punkt auf der Parabel .
Berechnen Sie die x-Koordinate des Punktes (2 P)
