Gemischte Aufgaben - lernen mit Serlo!

Gegeben sind die Eckpunkte einer Pyramide $A (0 | 0 | 0)$ , $B (6 | 0 | 0)$ , $C (6 | 6 | 0)$ , $D (0 | 6 | 0)$ , $S (3 | 3 | 12)$ und die Gleichung einer Ebene $K : 2 x_{2} + 4,5 x_{3} = 20$ . Die Pyramide wird von der Ebene $K$ geschnitten.

Zeige, dass die Schnittfläche zwischen Pyramide und Ebene ein gleichschenkliges (symmetrisches) Trapez ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Die folgende Skizze (nicht maßstabsgetreu) verdeutlicht die Aufgabenstellung und dient zur Orientierung bei der Benennung der Pyramidenpunkte.
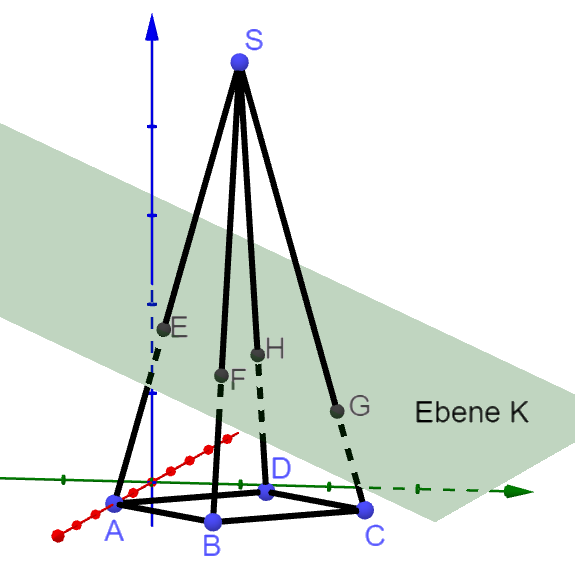
Berechne die Gleichungen der Pyramidenkanten
$g_{A S} : \vec{X} = \vec{A} + r \cdot (\vec{S} - \vec{A}) = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 0 \\ 3 - 0 \\ 12 - 0 \end{array})$
Kürze den Richtungsvektor mit Faktor $3$ :
$g_{A S} : \vec{X} = r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
$g_{B S} : \vec{X} = \vec{B} + r \cdot (\vec{S} - \vec{B}) = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 6 \\ 3 - 0 \\ 12 - 0 \end{array})$
Kürze den Richtungsvektor mit Faktor $3$ :
$g_{B S} : \vec{X} = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
$g_{C S} : \vec{X} = \vec{C} + r \cdot (\vec{S} - \vec{C}) = (\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 6 \\ 3 - 6 \\ 12 - 0 \end{array})$
Kürze den Richtungsvektor mit Faktor $3$ :
$g_{C S} : \vec{X} = (\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
$g_{D S} : \vec{X} = \vec{D} + r \cdot (\vec{S} - \vec{D}) = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 0 \\ 3 - 6 \\ 12 - 0 \end{array})$
Kürze den Richtungsvektor mit Faktor $3$ :
$g_{D S} : \vec{X} = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
Schneide die Geraden jeweils mit der Ebene $K$
$g_{A S} \cap K$ :
$g_{A S} : \vec{X} = r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
$K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
↓
Setze $x_{2} = r$ und $x_{3} = 4 r$ ein.
$2 \cdot r + 4,5 \cdot 4 r$ $=$ $20$
$2 r + 18 r$ $=$ $20$
$20 r$ $=$ $20$ $: 20$
$r$ $=$ $1$
Setze $r = 1$ in $g_{A S}$ ein, um die Koordinaten $E$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
$\vec{X}$ $=$ $r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
↓
Setze $r = 1$ ein.
$=$ $1 \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
↓
Vereinfache.
$=$ $(\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
Damit hat der Punkt $E$ die Koordinaten $E (1 | 1 | 4)$ .
$g_{B S} \cap K$ :
$g_{B S} : \vec{X} = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
$K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
↓
Setze $x_{2} = r$ und $x_{3} = 4 r$ ein.
$2 \cdot r + 4,5 \cdot 4 r$ $=$ $20$
$2 r + 18 r$ $=$ $20$
$20 r$ $=$ $20$ $: 20$
$r$ $=$ $1$
Setze $r = 1$ in $g_{B S}$ ein, um die Koordinaten $F$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
$\vec{X}$ $=$ $(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
↓
Setze $r = 1$ ein.
$=$ $(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
↓
Vereinfache.
$=$ $(\begin{array}{c} 5 \\ 1 \\ 4 \end{array})$
Damit hat der Punkt $F$ die Koordinaten $F (5 | 1 | 4)$ .
$g_{C S} \cap K :$
$g_{C S} : \vec{X} = (\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
$K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
↓
Setze $x_{2} = 6 - r$ und $x_{3} = 4 r$ ein.
$2 \cdot (6 - r) + 4,5 \cdot 4 r$ $=$ $20$
$12 - 2 r + 18 r$ $=$ $20$
$12 + 16 r$ $=$ $20$ $- 12$
$16 r$ $=$ $8$ $: 16$
$r$ $=$ $0,5$
Setze $r = 0,5$ in $g_{C S}$ ein, um die Koordinaten $G$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
$\vec{X}$ $=$ $(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
↓
Setze $r = 0,5$ ein.
$=$ $(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
↓
Vereinfache.
$=$ $(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$
Damit hat der Punkt $G$ die Koordinaten $G (5,5 | 5,5 | 2)$ .
$g_{D S} \cap K :$
$g_{D S} : \vec{X} = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
$K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
↓
Setze $x_{2} = 6 - r$ und $x_{3} = 4 r$ ein.
$2 \cdot (6 - r) + 4,5 \cdot 4 r$ $=$ $20$
$12 - 2 r + 18 r$ $=$ $20$
$12 + 16 r$ $=$ $20$ $- 12$
$16 r$ $=$ $8$ $: 16$
$r$ $=$ $0,5$
Setze $r = 0,5$ in $g_{D S}$ ein, um die Koordinaten $H$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
$\vec{X}$ $=$ $(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
↓
Setze $r = 0,5$ ein.
$=$ $(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
↓
Vereinfache.
$=$ $(\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
Damit hat der Punkt $H$ die Koordinaten $H (0,5 | 5,5 | 2)$ .
Die Schnittfläche
Die Punkte $E$ und $F$ haben die gleiche $x_{3}$ -Koordinate $4$ und die Punkte $G$ und $H$ haben die gleiche $x_{3}$ -Koordinate $2$ .
Berechne die Vektoren $\vec{E F} = \vec{F} - \vec{E}$ und $\vec{H G} = \vec{G} - \vec{H} :$
$\vec{E F}$ $=$ $(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
$=$ $(\begin{array}{c} 4 \\ 0 \\ 0 \end{array})$
$\vec{H G}$ $=$ $(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
$=$ $(\begin{array}{c} 5 \\ 0 \\ 0 \end{array})$
Damit folgt: $\vec{E F} ∥ \vec{H G}$
Die beiden Vektoren sind ungleich lang:
$| \vec{E F} | = \sqrt{4^{2} + 0^{2} + 0^{2}} = \sqrt{16} = 4$
$| \vec{H G} | = \sqrt{5^{2} + 0^{2} + 0^{2}} = \sqrt{25} = 5$
Berechne die Vektoren $\vec{G F} = \vec{F} - \vec{G}$ und $\vec{H E} = \vec{E} - \vec{H}$ :
$\vec{G F}$ $=$ $(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$
$=$ $(\begin{array}{c} - 0,5 \\ - 4,5 \\ 2 \end{array})$
$\vec{H E}$ $=$ $(\begin{array}{c} 1 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
$=$ $(\begin{array}{c} 0,5 \\ - 4,5 \\ 2 \end{array})$
Die Vektoren sind nicht parallel zueinander:
$(\begin{array}{c} - 0,5 \\ - 4,5 \\ 2 \end{array})$ $\neq$ $k \cdot (\begin{array}{c} 0,5 \\ - 4,5 \\ 2 \end{array})$
Aber die beiden Vektoren sind gleich lang:
$| \vec{G F} | = \sqrt{(- 0,5)^{2} + (- 4,5)^{2} + 2^{2}} = \sqrt{24,5}$
$| \vec{H E} | = \sqrt{(0,5)^{2} + (- 4,5)^{2} + 2^{2}} = \sqrt{24,5}$
Somit haben wir zwei ungleich lange parallele Vektoren $\vec{E F}$ und $\vec{H G}$ und zwei gleich lange, aber nicht parallele Vektoren $\vec{G F}$ und $\vec{H E}$ .
Die geometrische Figur kann demnach nur ein gleichschenkeliges (symmetrisches) Trapez und kein Parallelogramm sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Erstelle die Geradengleichungen für die vier Pyramidenkanten und schneide sie jeweils mit der Ebene $K$ , um die Eckpunkte der Schnittfläche zu erhalten.
Berechne den Flächeninhalt des Trapezes.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Für die Trapezfläche gilt:
$A_{Trapez} = \frac{a + c}{2} \cdot h$
Die Längen der beiden parallelen Seiten wurden in Aufgabe a) berechnet:
$a = | \vec{H G} | = 5$ und $c = | \vec{E F} | = 4$
Die Länge der Seite $| \vec{G F} | = \sqrt{24,5}$ .
Die Höhe des Trapezes muss noch berechnet werden:
Die Höhe $h$ kann mit dem Satz des Pythagoras berechnet werden.
Dazu muss erst die Länge der Seite x berechnet werden:
$x = 0,5 \cdot (5 - 4) = 0,5$
Dann gilt:
$h = \sqrt{| \vec{G F} |^{2} - x^{2}}$
$h = \sqrt{(\sqrt{24,5})^{2} - {0,5}^{2}}$
$h = \sqrt{24,25} \approx 4,925$
$A_{Trapez}$ $=$ $\frac{a + c}{2} \cdot h$
↓
Setze $a = 5$ , $c = 4$ und $h = 4,925$ ein.
$=$ $\frac{5 + 4}{2} \cdot 4,925$
$\approx$ $22,16$
Der Flächeninhalt des Trapezes beträgt etwa $22,16 FE$ .
Die folgende Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung.
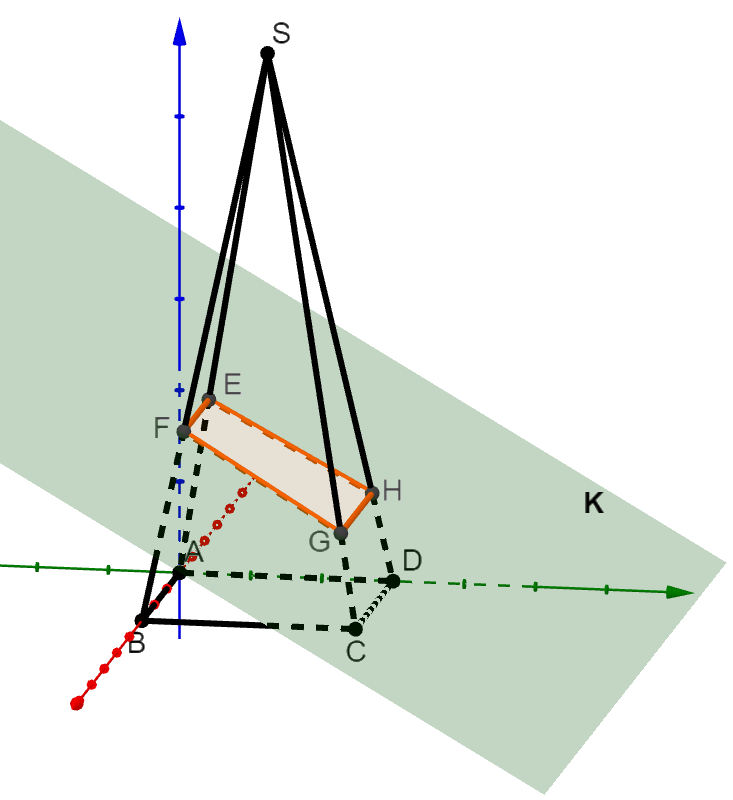
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$K : 2 x_{2} + 4,5 x_{3}$	$=$	$20$
	↓	Setze $x_{2} = r$ und $x_{3} = 4 r$ ein.
$2 \cdot r + 4,5 \cdot 4 r$	$=$	$20$
$2 r + 18 r$	$=$	$20$
$20 r$	$=$	$20$	$: 20$
$r$	$=$	$1$

$\vec{X}$	$=$	$r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
	↓	Setze $r = 1$ ein.
	$=$	$1 \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$

$\vec{X}$	$=$	$(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
	↓	Setze $r = 1$ ein.
	$=$	$(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 5 \\ 1 \\ 4 \end{array})$

$K : 2 x_{2} + 4,5 x_{3}$	$=$	$20$
	↓	Setze $x_{2} = 6 - r$ und $x_{3} = 4 r$ ein.
$2 \cdot (6 - r) + 4,5 \cdot 4 r$	$=$	$20$
$12 - 2 r + 18 r$	$=$	$20$
$12 + 16 r$	$=$	$20$	$- 12$
$16 r$	$=$	$8$	$: 16$
$r$	$=$	$0,5$

$\vec{X}$	$=$	$(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
	↓	Setze $r = 0,5$ ein.
	$=$	$(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$

$\vec{X}$	$=$	$(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
	↓	Setze $r = 0,5$ ein.
	$=$	$(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$

$\vec{E F}$	$=$	$(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
	$=$	$(\begin{array}{c} 4 \\ 0 \\ 0 \end{array})$

$\vec{H G}$	$=$	$(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
	$=$	$(\begin{array}{c} 5 \\ 0 \\ 0 \end{array})$

$\vec{G F}$	$=$	$(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$
	$=$	$(\begin{array}{c} - 0,5 \\ - 4,5 \\ 2 \end{array})$

$\vec{H E}$	$=$	$(\begin{array}{c} 1 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
	$=$	$(\begin{array}{c} 0,5 \\ - 4,5 \\ 2 \end{array})$

$A_{Trapez}$	$=$	$\frac{a + c}{2} \cdot h$
	↓	Setze $a = 5$ , $c = 4$ und $h = 4,925$ ein.
	$=$	$\frac{5 + 4}{2} \cdot 4,925$
	$\approx$	$22,16$

Berechne die Gleichungen der Pyramidenkanten

Schneide die Geraden jeweils mit der Ebene K

Die Schnittfläche

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schneide die Geraden jeweils mit der Ebene $K$