Gemischte Aufgaben

Hier findest du gemischte Übungsaufgaben zu Vektoren, Ebenen und vielem mehr. Schaffst du sie alle?

1
Berechne die Spurpunkte der gegebenen Geraden.
1. $g : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 3 \end{array}) + k \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte
  Spurpunkt in der $x_{1} x_{2}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{3}$ die Gleichung: $x_{3} = 3 - 2 k$
  Wird die $x_{1} x_{2}$ -Ebene geschnitten, so muss $x_{3} $ gleich Null sein: $x_{3} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 3 - 2 k & | + 2 k \\ 2 k & = & 3 & | : 2 \\ k & = & \frac{3}{2} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 3 \end{array}) + \frac{3}{2} \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4,5 \\ 3,5 \\ 0 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{2}} (4,5 ∣ 3,5 ∣ 0)$
  Spurpunkt in der $x_{1} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{2}$ die Gleichung: $x_{2} = 2 + k$
  Wird die $x_{1} x_{3}$ -Ebene geschnitten, so muss $x_{2} $ gleich Null sein: $x_{2} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 2 + k & | - 2 \\ k & = & - 2 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 3 \end{array}) + (- 2) \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 1 \\ 0 \\ 7 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{3}} (1 ∣ 0 ∣ 7)$
  Spurpunkt in der $x_{2} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{1}$ die Gleichung: $x_{1} = 3 + k$
  Wird die $x_{2} x_{3}$ -Ebene geschnitten, so muss $x_{1} $ gleich Null sein: $x_{1} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 3 + k & | - 3 \\ k & = & - 3 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 3 \\ 2 \\ 3 \end{array}) + (- 3) \cdot (\begin{array}{c} 1 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 0 \\ - 1 \\ 9 \end{array})$
  Antwort: Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{2} x_{3}} (0 ∣ - 1 ∣ 9)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Punkte, in denen die Gerade $g$ die Koordinatenebenen schneidet, heißen Spurpunkte. Berechne also jeweils den Schnittpunkt der Geraden $g$ mit einer der drei Koordinatenebenen.
2. $g : \vec{x} = (\begin{array}{c} 1 \\ - 1 \\ 0 \end{array}) + k \cdot (\begin{array}{c} 2 \\ 3 \\ 1 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte
  Spurpunkt in der $x_{1} x_{2}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{3}$ die Gleichung: $x_{3} = 0 + k$
  Wird die $x_{1} x_{2}$ -Ebene geschnitten, so muss $x_{3} $ gleich Null sein: $x_{3} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 0 + k \\ k & = & 0 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 1 \\ - 1 \\ 0 \end{array}) + 0 \cdot (\begin{array}{c} 2 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} 1 \\ - 1 \\ 0 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{2}} (1 ∣ - 1 ∣ 0)$
  Spurpunkt in der $x_{1} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{2}$ die Gleichung: $x_{2} = - 1 + 3 k$
  Wird die $x_{1} x_{3}$ -Ebene geschnitten, so muss $x_{2} $ gleich Null sein: $x_{2} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & - 1 + 3 k & | + 1 \\ 1 & = & 3 k & | : 3 \\ k & = & \frac{1}{3} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 1 \\ - 1 \\ 0 \end{array}) + \frac{1}{3} \cdot (\begin{array}{c} 2 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} \frac{5}{3} \\ 0 \\ \frac{1}{3} \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{3}} (\frac{5}{3} ∣ 0 ∣ \frac{1}{3})$
  Spurpunkt in der $x_{2} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{1}$ die Gleichung: $x_{1} = 1 + 2 k$
  Wird die $x_{2} x_{3}$ -Ebene geschnitten, so muss $x_{1} $ gleich Null sein: $x_{1} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 1 + 2 k & | - 1 \\ - 1 & = & 2 k & | : 2 \\ k & = & - \frac{1}{2} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 1 \\ - 1 \\ 0 \end{array}) + (- \frac{1}{2}) \cdot (\begin{array}{c} 2 \\ 3 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ - \frac{5}{2} \\ - \frac{1}{2} \end{array})$
  Antwort: Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{2} x_{3}} (0 ∣ - \frac{5}{2} ∣ - \frac{1}{2})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Punkte, in denen die Gerade $g$ die Koordinatenebenen schneidet, heißen Spurpunkte. Berechne also jeweils den Schnittpunkt der Geraden $g$ mit einer der drei Koordinatenebenen.
3. $g : \vec{x} = (\begin{array}{c} - 2 \\ 4 \\ 1 \end{array}) + k \cdot (\begin{array}{c} - 2 \\ - 1 \\ 3 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte
  Spurpunkt in der $x_{1} x_{2}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{3}$ die Gleichung: $x_{3} = 1 + 3 k$
  Wird die $x_{1} x_{2}$ -Ebene geschnitten, so muss $x_{3} $ gleich Null sein: $x_{3} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 1 + 3 k & | - 3 k \\ - 3 k & = & 1 & | : (- 3) \\ k & = & - \frac{1}{3} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} - 2 \\ 4 \\ 1 \end{array}) + (- \frac{1}{3}) \cdot (\begin{array}{c} - 2 \\ - 1 \\ 3 \end{array}) = (\begin{array}{c} - \frac{4}{3} \\ \frac{13}{3} \\ 0 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{2}} (- \frac{4}{3} ∣ \frac{13}{3} ∣ 0)$
  Spurpunkt in der $x_{1} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{2}$ die Gleichung: $x_{2} = 4 - k$
  Wird die $x_{1} x_{3}$ -Ebene geschnitten, so muss $x_{2} $ gleich Null sein: $x_{2} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 4 - k & | + k \\ k & = & 4 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} - 2 \\ 4 \\ 1 \end{array}) + 4 \cdot (\begin{array}{c} - 2 \\ - 1 \\ 3 \end{array}) = (\begin{array}{c} - 10 \\ 0 \\ 13 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{3}} (- 10 ∣ 0 ∣ 13)$
  Spurpunkt in der $x_{2} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{1}$ die Gleichung: $x_{1} = - 2 - 2 k$
  Wird die $x_{2} x_{3}$ -Ebene geschnitten, so muss $x_{1} $ gleich Null sein: $x_{1} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & - 2 - 2 k & | + 2 k \\ 2 k & = & - 2 & | : 2 \\ k & = & - 1 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} - 2 \\ 4 \\ 1 \end{array}) + (- 1) \cdot (\begin{array}{c} - 2 \\ - 1 \\ 3 \end{array}) = (\begin{array}{c} 0 \\ 5 \\ - 2 \end{array})$
  Antwort: Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{2} x_{3}} (0 ∣ 5 ∣ - 2)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Punkte, in denen die Gerade $g$ die Koordinatenebenen schneidet, heißen Spurpunkte. Berechne also jeweils den Schnittpunkt der Geraden $g$ mit einer der drei Koordinatenebenen.
4. $g : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 5 \end{array}) + k \cdot (\begin{array}{c} 1 \\ - 4 \\ 2 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte
  Spurpunkt in der $x_{1} x_{2}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{3}$ die Gleichung: $x_{3} = - 5 + 2 k$
  Wird die $x_{1} x_{2}$ -Ebene geschnitten, so muss $x_{3} $ gleich Null sein: $x_{3} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & - 5 + 2 k & | - 2 k \\ - 2 k & = & - 5 & | : (- 2) \\ k & = & \frac{5}{2} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 5 \end{array}) + \frac{5}{2} \cdot (\begin{array}{c} 1 \\ - 4 \\ 2 \end{array}) = (\begin{array}{c} 6,5 \\ - 8 \\ 0 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{2}} (6,5 ∣ - 8 ∣ 0)$
  Spurpunkt in der $x_{1} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{2}$ die Gleichung: $x_{2} = 2 - 4 k$
  Wird die $x_{1} x_{3}$ -Ebene geschnitten, so muss $x_{2} $ gleich Null sein: $x_{2} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 2 - 4 k & | + 4 k \\ 4 k & = & 2 & | : 4 \\ k & = & \frac{1}{2} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 5 \end{array}) + (\frac{1}{2}) \cdot (\begin{array}{c} 1 \\ - 4 \\ 2 \end{array}) = (\begin{array}{c} 4,5 \\ 0 \\ - 4 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{3}} (4,5 ∣ 0 ∣ - 4)$
  Spurpunkt in der $x_{2} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{1}$ die Gleichung: $x_{1} = 4 + k$
  Wird die $x_{2} x_{3}$ -Ebene geschnitten, so muss $x_{1} $ gleich Null sein: $x_{1} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 4 + k & | - 4 \\ k & = & - 4 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 5 \end{array}) + (- 4) \cdot (\begin{array}{c} 1 \\ - 4 \\ 2 \end{array}) = (\begin{array}{c} 0 \\ 18 \\ - 13 \end{array})$
  Antwort: Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{2} x_{3}} (0 ∣ 18 ∣ - 13)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Punkte, in denen die Gerade $g$ die Koordinatenebenen schneidet, heißen Spurpunkte. Berechne also jeweils den Schnittpunkt der Geraden $g$ mit einer der drei Koordinatenebenen.
5. $g : \vec{x} = (\begin{array}{c} - 3 \\ 2 \\ 5 \end{array}) + k \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte
  Spurpunkt in der $x_{1} x_{2}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{3}$ die Gleichung: $x_{3} = 5 + 0 k = 5$
  Wird die $x_{1} x_{2}$ -Ebene geschnitten, so muss $x_{3} $ gleich Null sein: $x_{3} = 0 \Rightarrow$
  $0 = 5$
  Das ist eine falsche Aussage.
  Antwort: Es gibt keinen Schnittpunkt mit der $x_{1} x_{2}$ -Ebene. Die Gerade verläuft parallel zur $x_{1} x_{2}$ -Ebene.
  Spurpunkt in der $x_{1} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{2}$ die Gleichung: $x_{2} = 2 + k$
  Wird die $x_{1} x_{3}$ -Ebene geschnitten, so muss $x_{2} $ gleich Null sein: $x_{2} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 2 + k & | - 2 \\ k & = & - 2 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} - 3 \\ 2 \\ 5 \end{array}) + (- 2) \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} - 7 \\ 0 \\ 5 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{3}} (- 7 ∣ 0 ∣ 5)$
  Spurpunkt in der $x_{2} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{1}$ die Gleichung: $x_{1} = - 3 + 2 k$
  Wird die $x_{2} x_{3}$ -Ebene geschnitten, so muss $x_{1} $ gleich Null sein: $x_{1} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & - 3 + 2 k & | + 3 \\ 3 & = & 2 k & | : 2 \\ k & = & \frac{3}{2} \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} - 3 \\ 2 \\ 5 \end{array}) + \frac{3}{2} \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 3,5 \\ 5 \end{array})$
  Antwort: Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{2} x_{3}} (0 ∣ 3,5 ∣ 5)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Punkte, in denen die Gerade $g$ die Koordinatenebenen schneidet, heißen Spurpunkte. Berechne also jeweils den Schnittpunkt der Geraden $g$ mit einer der drei Koordinatenebenen.
6. $g : \vec{x} = (\begin{array}{c} 2 \\ 0 \\ 1 \end{array}) + k \cdot (\begin{array}{c} 1 \\ 0 \\ 1 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spurpunkte
  Spurpunkt in der $x_{1} x_{2}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{3}$ die Gleichung: $x_{3} = 1 + k$
  Wird die $x_{1} x_{2}$ -Ebene geschnitten, so muss $x_{3} $ gleich Null sein: $x_{3} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 1 + k & | - 1 \\ k & = & - 1 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 2 \\ 0 \\ 1 \end{array}) + (- 1) \cdot (\begin{array}{c} 1 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 1 \\ 0 \\ 0 \end{array})$
  Antwort: Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten:
  $S_{x_{1} x_{2}} (1 ∣ 0 ∣ 0)$
  Spurpunkt in der $x_{1} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{2}$ die Gleichung: $x_{2} = 0 + 0 k = 0$
  Wird die $x_{1} x_{3}$ -Ebene geschnitten, so muss $x_{2} $ gleich Null sein: $x_{2} = 0 \Rightarrow$
  $0 = 0$
  Das ist eine wahre Aussage. Es gibt unendliche viele Schnittpunkte mit der $x_{1} x_{3}$ -Ebene .
  Antwort: Die Gerade $g$ verläuft ganz in der $x_{1} x_{3}$ -Ebene.
  Spurpunkt in der $x_{2} x_{3}$ -Ebene
  Der Geradengleichung $g$ entnimmst du für $x_{1}$ die Gleichung: $x_{1} = 2 + k$
  Wird die $x_{2} x_{3}$ -Ebene geschnitten, so muss $x_{1} $ gleich Null sein: $x_{1} = 0 \Rightarrow$
  $\begin{array}{rcl} 0 & = & 2 + k & | - 2 \\ k & = & - 2 \end{array}$
  Das berechnete $k$ wird in die Geradengleichung $g$ eingesetzt und ergibt den Vektor zum Spurpunkt.
  $g : \vec{x} = (\begin{array}{c} 2 \\ 0 \\ 1 \end{array}) + (- 2) \cdot (\begin{array}{c} 1 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ - 1 \end{array})$
  Antwort: Der Spurpunkt in der $x_{2} x_{3}$ -Ebene hat die Koordinaten:
  $S_{x_{2} x_{3}} (0 ∣ 0 ∣ - 1)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Punkte, in denen die Gerade $g$ die Koordinatenebenen schneidet, heißen Spurpunkte. Berechne also jeweils den Schnittpunkt der Geraden $g$ mit einer der drei Koordinatenebenen.
2
Ein Dreieck ABC ist gegeben durch die Punkte $A (2 | - 3 | - 4), B (1 | 5 | 0), C (3 | 1 | 4)$ .
1. Bestimme den Umfang des Dreiecks.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Punkte berechnen
  Länge der Strecken
  Setze jeweils die Koordinaten der Punkte in den "dreidimensionalen Pythagoras" ein:
  $P R = \sqrt{(p_{1} - r_{1})^{2} + (p_{2} - r_{2})^{2} + (p_{3} - r_{3})^{2}}$
  Strecke $A B$ :
  $A B = \sqrt{(2 - 1)^{2} + (- 3 - 5)^{2} + (- 4 - 0)^{2}} L E = 9 L E$
  Strecke $A C$ :
  $A C = \sqrt{(2 - 3)^{2} + (- 3 - 1)^{2} + (- 4 - 4)^{2}} L E = 9 L E$
  Strecke $C B :$
  $C B = \sqrt{(3 - 1)^{2} + (1 - 5)^{2} + (4 - 0)^{2}} L E = 6 L E$
  Umfang des Dreiecks
  Addiere die Streckenlängen
  $U = A B + A C + C B = 9 L E + 9 L E + 6 L E = 24 L E$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Umfang enstspricht der Summe der Abstände der drei Punkte zueinander. (Alternativ kann man auch die Länge der Verbindungsvektoren bestimmen.)
2. Handelt es sich um ein besonderes Dreieck (Mehrfachauswahl möglich)?
  Das Dreieck ist rechtwinklig
  Das Dreieck ist gleichseitig
  Das Dreieck ist gleichschenklig
  Nein, es ist kein besonderes Dreieck
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: besondere Dreiecke
  Das Dreieck ist gleichschenklig mit der Basis $[B C]$ , da die zwei Seiten $[A B]$ und $[A C]$ gleich lang sind.
  Wäre das Dreieck gleichseitig, müsste auch die Strecke $B C$ 9 LE lang sein.
  Damit ein Dreieck rechtwinklig ist, muss der Umkehrsatz des Satz des Pythagoras gelten, also für die gegebenen Seitenlängen 6 LE, 9 LE und 9 LE die Beziehung $a^{2} + b^{2} = c^{2}$ erfüllt sein, wobei c die eindeutig längste Seite ist. Da aber zwei Seiten 9 LE lang sind, kann das Dreieck diese Beziehung nicht erfüllen und ist folglich nicht rechtwinklig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Schau dir die Seitenlängen des Dreiecks an.
3
Ein Wandergebiet ist von vielen Wanderwegen durchzogen. Legt man dieses Wandergebiet in ein Koordinatensystem, so kann man seine Zielposition mithilfe von Vektorketten berechnen.
Du beginnst eine Wanderung an einem Parkplatz, der ausgehend vom Ursprung die Koordinaten $P (1 | - 2 | 0,5)$ hat. Danach bewegst du dich 2,7 km entlang eines Weges, der durch den Vektor $\vec{w_{1}} = (\begin{array}{c} 8 \\ 4 \\ 1 \end{array})$ ausgedrückt wird, bevor du vorzeitig auf einen anderen Weg $\vec{w_{2}} = (\begin{array}{c} - 11 \\ - 10 \\ 2 \end{array})$ abbiegst und diesem 1,5 km folgst. Danach steigst du in eine Talbahn und fährst 1,8 km einen Weg entlang, der im Koordinatensystem durch $\vec{w_{3}} = (\begin{array}{c} 1 \\ 8 \\ - 4 \end{array})$ beschrieben wird, bevor du an einer Zwischenstation aussteigst.
1. Bestimme die Koordinaten des Berggasthofes $B$ , bei dem du deine Wanderung beendest.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge von Vektoren anpassen
  Der zu berechnende Term
  Um zum Berggasthof zu gelangen, muss man vom Parkplatz aus die veränderten Vektoren, die den Wanderwegen entsprechen, abgehen.
  Keine Angst, der Term wird in den nächsten Schritten nochmal Stück für Stück aufgeschlüsselt und erklärt.
  $\vec{B} = \vec{P} + \frac{2,7}{| \vec{w_{1}} |} \cdot \vec{w_{1}} + \frac{1,5}{| \vec{w_{2}} |} \cdot \vec{w_{2}} + \frac{1,8}{| \vec{w_{3}} |} \cdot \vec{w_{3}}$
  Länge der Wege berechnen
  Um jeden Weg auf die gewünschte Länge $k$ zu verkürzen, muss man ihn erst auf die Länge 1 verkürzen und dann wieder auf die Länge $k$ strecken. Dafür berechnest du zuerst die Länge jedes Weges, also die Länge der Vektoren.
  $| \vec{w_{1}} | = \sqrt{8^{2} + 4^{2} + 1^{2}} L E = 9 L E$
  $| \vec{w_{2}} | = \sqrt{{(- 11)}^{2} + {(- 10)}^{2} + 2^{2}} L E = 15 L E$
  $| \vec{w_{3}} | = \sqrt{1^{2} + 8^{2} + {(- 4)}^{2}} L E = 9 L E$
  Wege verkürzen
  Den Quotienten aus gewünschter Länge $k_{1,2,3}$ und aktueller Länge $| {\vec{w}}_{1,2,3} |$ multiplizierst du jetzt bei einer skalaren Multiplikation mit dem jeweiligen Vektor ${\vec{w}}_{1,2,3}$ . Zur Übersicht kannst du die berechneten Vektoren noch benennen. Hier benennen wir sie mit $\vec{z_{1}}, \vec{z_{2}}, \vec{z_{3}}$ für "zurückgelegter Weg".
  $\vec{z_{1}} = \frac{k_{1}}{| \vec{w_{1}} |} \cdot \vec{w_{1}} = \frac{2,7}{9} \cdot (\begin{array}{c} 8 \\ 4 \\ 1 \end{array}) = 0,3 \cdot (\begin{array}{c} 8 \\ 4 \\ 1 \end{array}) = (\begin{array}{c} 2,4 \\ 1,2 \\ 0,3 \end{array})$
  $\vec{z_{2}} = \frac{k_{2}}{| \vec{w_{2}} |} \cdot \vec{w_{2}} = \frac{1,5}{15} \cdot (\begin{array}{c} - 11 \\ - 10 \\ 2 \end{array}) = 0,1 \cdot (\begin{array}{c} - 11 \\ - 10 \\ 2 \end{array}) = (\begin{array}{c} - 1,1 \\ - 1 \\ 0,2 \end{array})$
  $\vec{z_{3}} = \frac{k_{3}}{| \vec{w_{3}} |} \cdot \vec{w_{3}} = \frac{1,8}{9} \cdot (\begin{array}{c} 1 \\ 8 \\ - 4 \end{array}) = 0,2 \cdot (\begin{array}{c} 1 \\ 8 \\ - 4 \end{array}) = (\begin{array}{c} 0,2 \\ 1,6 \\ - 0,8 \end{array})$
  Vektorkette bilden
  Nun kannst du die Vektoren in die Vektorkette oben einsetzen und die Koordinaten des Berggasthofes bestimmen.
  $\vec{B} = \vec{P} + \frac{2,7}{| \vec{w_{1}} |} \cdot \vec{w_{1}} + \frac{1,5}{| \vec{w_{2}} |} \cdot \vec{w_{2}} + \frac{1,8}{| \vec{w_{3}} |} \cdot \vec{w_{3}}$
  Setze zunächst an den zugehörigen Stellen die Vektoren ${\vec{z}}_{1}, {\vec{z}}_{2}, {\vec{z}}_{3}$ ein:
  $\vec{B} = \vec{P} + {\vec{z}}_{1} + {\vec{z}}_{2} + {\vec{z}}_{3}$
  Berechne nun den Wert des Terms, in dem du die Vektoren addierst:
  $\vec{B} = (\begin{array}{c} 1 \\ - 2 \\ 0,5 \end{array}) + (\begin{array}{c} 2,4 \\ 1,2 \\ 0,3 \end{array}) + (\begin{array}{c} - 1,1 \\ - 1 \\ 0,2 \end{array}) + (\begin{array}{c} 0,2 \\ 1,6 \\ - 0,8 \end{array}) = (\begin{array}{c} 2,5 \\ - 0,2 \\ 0,2 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Hier musst du einiges an Wissen verknüpfen:
  Der Weg vom Parkplatz zum Gasthof ist eine Vektorkette und beginnt mit dem Ortsvektor des Parkplatzes.
  Die Wege werden dabei nicht komplett durchlaufen, sondern es wird vorher abgebogen. Man muss die Vektoren also geeignet verkürzen.
2. Bei Wanderungen gibt man häufig an, wie viele Höhenmeter es nach oben $(↗ . . . m)$ beziehungsweise nach unten $(↙ . . . m)$ geht. Wie ist es bei dieser Wanderung?
  Wie würdest du die Schwierigkeit der Wanderung einschätzen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
  Mit dem Auto startet man auf einer Höhe von 500 m.
  Die ersten beiden Wege führen bergauf, nämlich 0,2 km + 0,3 km, also insgesamt $↗ 500 m$
  Der dritte Weg führt bergab, nämlich 0,8 km, allerdings werden diese nicht gelaufen (viel zu steil!) sondern mit einer Talbahn zurückgelegt. Man kann sich jetzt also streiten, ob man $↙ 0 m$ oder $↙ 800 m$ angibt.
  Schwierigkeit der Route
  Der Wanderweg hat recht große Steigungen und ist deshalb definitiv nichts für Anfänger, obwohl er nicht lang ist!
  Im ersten Wegstück wird zum Beispiel auf 2,7 km Strecke 0,3 km Höhe gewonnen, was einer Steigung von durchgehend mehr als 10% entspricht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die x-3-Koordinate gibt an, wie viele Meter man nach oben bzw unten wandert.
3. Stelle die durchlaufene Wanderung in einem geeigneten Koordinatensystem dar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
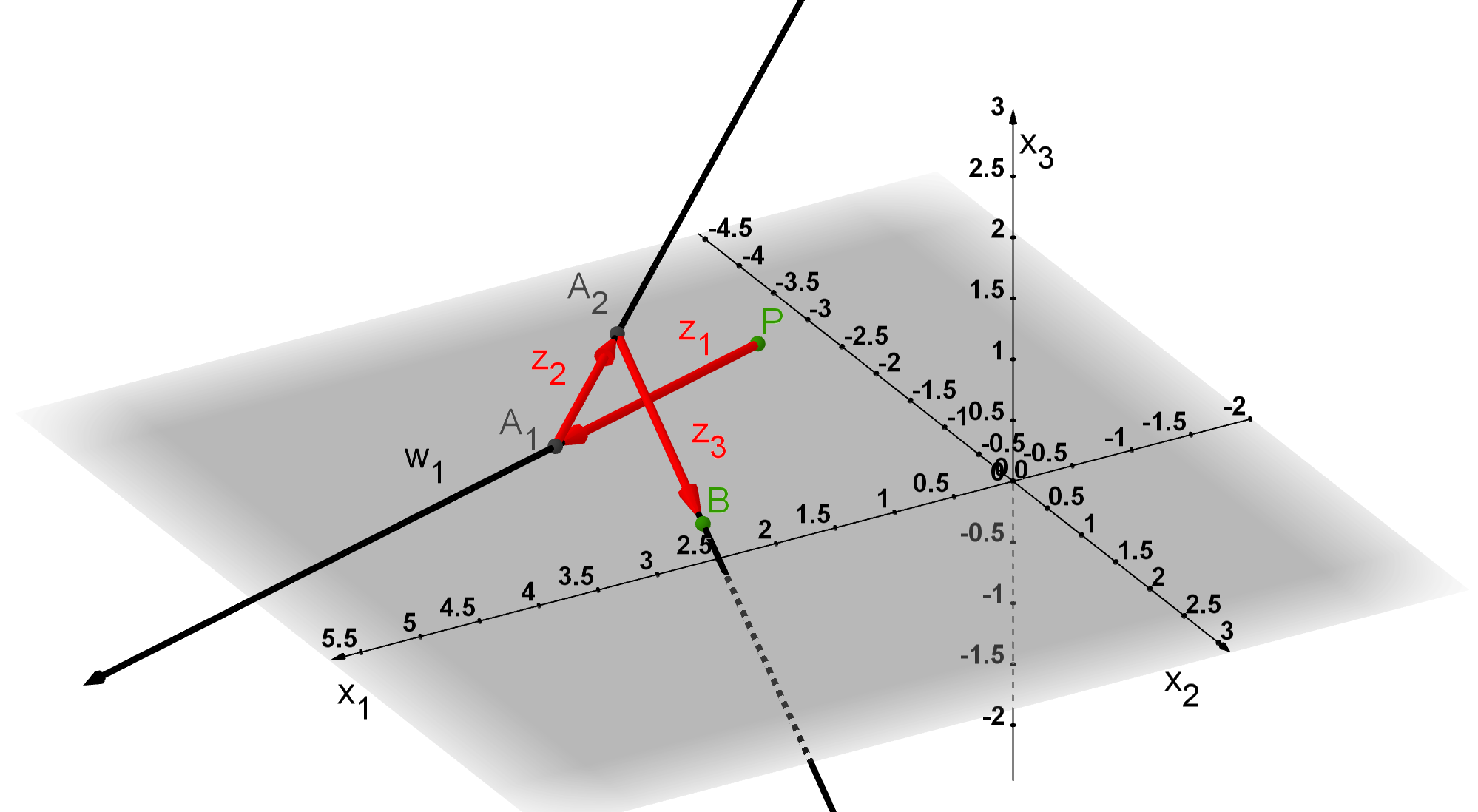
  Vom Punkt P aus wird zuerst der Vektor ${\vec{z}}_{1}$ aus Aufgabe a) angehängt und an dessen Spitze dann noch die beiden anderen. am Schluss markiert man den Punkt B.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Da du in Teilaufgabe a) bereits die Vektoren berechnet hast, die du vom Punkt P aus durchläufst, musst du diese jetzt nur noch in ein Koordinatensystem malen.
4
Überlege und begründe, ob die vier Ebenen ein Volumen einschließen, und berechne dieses gegebenenfalls.
1. $E_{1} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $E_{2} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 3 \\ 2 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 4 \\ 5 \\ 6 \end{array})] = 0$
  $E_{3} : \frac{1}{\sqrt{101}} (\begin{array}{c} 6 \\ 7 \\ 4 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 4 \\ 5 \\ 6 \end{array})] = 0$
  $E_{4} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 3 \\ 2 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})] = 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hessesche Normalenform
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ebene 2 und Ebene 4 sind parallel zueinander. Man kann sich überlegen, dass man dann mindestens drei weitere Ebenen braucht, um ein Volumen einzuschließen.
  Wenn wir ein Zimmer mit einer Decke und einem Boden haben (die parallel zueinander sind), braucht man ja auch mindestens 3 (ebene) Wände, um ein richtiges Zimmer zu haben.
2. $E_{1} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $E_{2} : \frac{1}{\sqrt{14}} (\begin{array}{c} - 1 \\ 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $E_{3} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $E_{4} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hessesche Normalenform
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Punkt $A (1 | 2 | 3)$ liegt in allen vier Ebenen. Man kann sich bildlich überlegen, dass die Ebenen dann kein Volumen einschließen können.
  Eine Beweisidee ginge zum Beispiel so:
  Wenn wir ein eingeschlossenes Volumen hätten und der Punkt $B (e | f | g)$ eingeschlossen wäre, würde jede Gerade, die durch den Punkt B geht, mindesten zwei unterschiedliche Schnittpunkte mit den Ebenen haben. Da die Gerade durch die Ränder des eingeschlossenen Volumens geht. Betrachten wir die Gerade, die durch die Punkte A und B geht.
  $g : (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + λ (\begin{array}{c} e - 1 \\ f - 2 \\ g - 3 \end{array})$
  Die Gerade schneidet alle Ebenen in dem Punkt A. Wir wissen, dass jede Gerade eine Ebene nur ein mal schneiden kann (oder Teil von ihr ist). Also gibt es keinen anderen Schnittpunkt mit den Ebenen und der Geraden $g$ . Also gibt es keinen anderen Rand vom eingeschlossen Volumen, also kann B in keinem eingeschlossenen Volumen sein, was ein Widerspruch ist.
3. $E_{1} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $E_{2} : \frac{1}{\sqrt{14}} (\begin{array}{c} - 1 \\ 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 4 \\ 5 \\ 6 \end{array})] = 0$
  $E_{3} : \frac{1}{\sqrt{6}} (\begin{array}{c} 0 \\ 0 \\ 6 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 7 \\ 8 \\ 9 \end{array})] = 0$
  $E_{4} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 1 \end{array})] = 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen zwischen 3 Ebenen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Man sieht, dass die Normalenvektoren der ersten drei Ebenen linear abhängig voneinander sind.
  $(\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) + (\begin{array}{c} - 1 \\ 2 \\ 3 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ 6 \end{array})$
  Das bedeutet insbesondere, dass die drei Normalenvektoren in einer Ebenen liegen. Bestimmen wir von dieser Ebene jetzt wiederum den Normalenvektor:
  $(\begin{array}{c} 0 \\ 0 \\ 6 \end{array}) \times (\begin{array}{c} - 1 \\ 2 \\ 3 \end{array}) = (\begin{array}{c} 0 \cdot 3 - 6 \cdot 2 \\ 6 \cdot (- 1) - 0 \cdot 3 \\ 0 \cdot 2 - 0 \cdot (- 1) \end{array}) = (\begin{array}{c} - 12 \\ - 6 \\ 0 \end{array})$
  Dieser Vektor ist für unser Problem entscheidend!
  Betrachten wir die Geradenschar $g$ , die von diesem Vektor aufgespannt wird:
  $g : (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{c} e \\ f \\ g \end{array}) + λ (\begin{array}{c} - 12 \\ - 6 \\ 0 \end{array})$
  Jede dieser Geraden ist parallel zu den ersten drei Ebenen dieser Teilaufgabe (oder Teil von mindesten einer der Ebenen). Denn die Geradenschar ist ja grade so festgelegt, dass der Span-Vektor senkrecht auf den Normalenvektoren der ersten drei Ebenen steht. Was die Bedingung für Parallelität von Gerade und Ebene ist.
  Wenn jetzt der Punkt $P (a | b | c)$ Teil eines eingeschlossenen Gebiets ist, muss jede Gerade, die durch den Punkt P geht, mindesten zwei Ebenen der vier gegebenen Ebenen schneiden, da es jede Gerade sein muss, können wir auch eine aus der Geradenschar $g$ nehmen.
  $g_{P} : (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{c} a \\ b \\ c \end{array}) + λ (\begin{array}{c} - 12 \\ - 6 \\ 0 \end{array})$
  Diese Gerade schneidet jedoch die Ebenen $E_{1}$ , $E_{2}$ und $E_{3}$ nicht. Also kann sie nur die Ebene 4 schneiden. Diese kann sie jedoch nur ein mal schneiden. Also kann der allgemeine Punkt nicht Teil eines eingeschlossenen Volumens sein. Also gibt es keine eingeschlossenen Volumen.
  Räumlich kann man sich vorstellen, dass die Ebenen $E_{1}$ , $E_{2}$ und $E_{3}$ einen unendlich langen geraden Tunnel erzeugen, diesen kann man nicht mit einer Wand (Ebenen) zu einem Zimmer machen.
4. $E_{1} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $E_{2} : \frac{1}{\sqrt{14}} (\begin{array}{c} - 1 \\ 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 4 \\ 5 \\ 6 \end{array})] = 0$
  $E_{3} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 7 \\ 8 \\ 9 \end{array})] = 0$
  $E_{4} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})] = 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung in der analytischen Geometrie
  Um die Schnittpunkte der Ebenen zu bestimmen, bringst du zunächst die Ebenen in Koordinatenform:
  $E_{1} : \frac{1}{\sqrt{14}} (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0$
  $\begin{array}{l} E_{1} : (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) \circ [(\begin{array}{c} x_{1} - 1 \\ x_{2} - 2 \\ x_{3} - 3 \end{array})] = 0 \\ E_{1} : 1 \cdot (x_{1} - 1) + (- 2) \cdot (x_{2} - 2) + 3 \cdot (x_{3} - 3) = 0 \\ E_{1} : (x_{1} - 1) + (- 2 x_{2} + 4) + (3 x_{3} - 9) = 0 \\ E_{1} : x_{1} - 2 x_{2} + 3 x_{3} = 6 \end{array}$
  Analog:
  $E_{2} : - x_{1} + 2 x_{2} + 3 x_{3} = 24$
  $E_{3} : x_{1} + 2 x_{2} - 3 x_{3} = - 4$
  $ E_{4} : x_{1} + 2 x_{2} + 3 x_{3} = 0$
  Jetzt bestimmst du $A (x_{1} | x_{2} | x_{3})$ als Schnittpunkt der Ebenen $E_{1}$ , $E_{2}$ und $E_{3}$ .
  Diese geschieht, indem du die drei Ebenen als Gleichungen eines linearen Gleichungssystems auffasst. In diesem Beispiel kann man sie addieren, um die Unbekannten zu bestimmen.
  $E_{1} + E_{2} \Rightarrow 6 x_{3} = 30 \Rightarrow x_{3} = 5$
  $E_{1} + E_{3} \Rightarrow 2 x_{1} = 2 \Rightarrow x_{1} = 1$
  $E_{2} + E_{3} \Rightarrow 4 x_{2} = 20 \Rightarrow x_{2} = 5$
  Somit ist der Punkt $A (1 | 5 | 5)$ eindeutig bestimmt.
  Analog lassen sich
  $B (- 12 | 5 | \frac{2}{3})$ als Schnittpunkt der Ebenen $E_{2}$ , $E_{3}$ und $E_{4}$ ,
  $C (- 12 | - \frac{3}{2} | 5)$ als Schnittpunkt der Ebenen $E_{1}$ , $E_{2}$ und $E_{4}$ und
  $D (1 | - \frac{3}{2} | \frac{2}{3})$ als Schnittpunkt der Ebenen $E_{1}$ , $E_{3}$ und $E_{4}$ bestimmen.
  Setze jetzt in die Volumenformel ein:
  $\begin{array}{l} V = \frac{1}{6} | \det (\vec{A B}, \vec{A C}, \vec{A D}) | \\ = \frac{1}{6} | \det ((\begin{array}{c} - 12 \\ 5 \\ \frac{2}{3} \end{array}) - (\begin{array}{c} 1 \\ 5 \\ 5 \end{array}), (\begin{array}{c} - 12 \\ - \frac{3}{2} \\ 5 \end{array}) - (\begin{array}{c} 1 \\ 5 \\ 5 \end{array}), (\begin{array}{c} 1 \\ - \frac{3}{2} \\ \frac{2}{3} \end{array}) - (\begin{array}{c} 1 \\ 5 \\ 5 \end{array})) | \end{array}$
  $= \frac{1}{6} | \det ((\begin{array}{c} - 13 \\ 0 \\ - \frac{13}{3} \end{array}), (\begin{array}{c} - 13 \\ - \frac{13}{2} \\ 0 \end{array}), (\begin{array}{c} 0 \\ - \frac{13}{2} \\ - \frac{13}{3} \end{array})) |$
  $= \frac{1}{6} | - 13 \cdot (- \frac{13}{2}) \cdot (- \frac{13}{3}) + (- 13) \cdot (- \frac{13}{2}) \cdot (- \frac{13}{3}) + 0 - 0 - 0 - 0 |$
  $= \frac{1}{6} | - 13^{3} \cdot \frac{1}{3} |$
  $= \frac{2197}{18}$
  $\approx 122$
  Das eingeschlossene Volumen ist etwa $122$ $VE$ groß.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Körper, der entsteht, wenn wir vier Ebenen schneiden, ist eine Pyramide mit vier Seiten, also ein Tetraeder.
  Das Volumen eines Tetraeders berechnet man in der analytischen Geometrie am einfachsten über die Determinante der aufspannenden Vektoren:
  $V = \frac{1}{6} | \det (\vec{A B}, \vec{A C}, \vec{A D}) |,$
  wobei die Punkte $A$ , $B$ , $C$ und $D$ die Eckpunkte des Tetraeders sind. Diese sind in unserem Fall auch die Punkte an denen sich jeweils drei Ebenen schneiden.

Gegeben sind die Punkte $A (6 | 0 | 3)$ , $B (6 | 4 | 0)$ und $C (0 | 6 | 1,5)$ .

Zeige, dass die drei Punkte $A$ , $B$ , und $C$ nicht auf einer Geraden liegen.

Bestimme eine Parametergleichung der Ebene, die durch die Punkte $A$ , $B$ , und $C$ verläuft.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parametergleichung einer Ebene
Ebenengleichung $E_{A B C}$ durch die Punkte $A$ , $B$ und $C$ :
$E_{A B C} : \vec{X} = \vec{A} + r \cdot \vec{A B} + s \cdot \vec{A C}$
Der Vektor $\vec{A B}$ wurde in Aufgabe a) berechnet:
$\vec{A B} = (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array})$
Berechne nun den Vektor $\vec{A C}$ :
$\vec{A C} = \vec{C} - \vec{A} = (\begin{array}{c} 0 \\ 6 \\ 1,5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 3 \end{array}) = (\begin{array}{c} - 6 \\ 6 \\ - 1,5 \end{array})$
Setze alle Vektoren in die Ebenengleichung ein:
$E_{A B C} : \vec{X} = (\begin{array}{c} 6 \\ 0 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array}) + s \cdot (\begin{array}{c} - 6 \\ 6 \\ - 1,5 \end{array})$
Das ist die gesuchte Parameterform der Ebene $E_{A B C}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Wandle die Parameterform der Ebene $E_{A B C}$ in eine Koordinatenform um.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parameterform in Koordinatenform umwandeln
Um eine Ebene von der Parameterform in die entsprechende Koordinatenform umzuwandeln, muss man nacheinander folgende Umwandlungen vornehmen:
Parameterform in Normalenform
Normalenform in Koordinatenform
Schritt 1: Umwandlung in die Normalenform

$E : (\vec{X} - \vec{A}) \circ \vec{n} = 0$
Berechne den Normalenvektor $\vec{n}$ als Vektorprodukt der beiden Richtungsvektoren:
$\vec{n} = (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array}) \times (\begin{array}{c} - 6 \\ 6 \\ - 1,5 \end{array}) = (\begin{array}{c} 4 \cdot (- 1,5) - (- 3) \cdot 6 \\ (- 3) \cdot (- 6) - 0 \cdot (- 1,5) \\ 0 \cdot 6 - 4 \cdot (- 6) \end{array}) = (\begin{array}{c} 12 \\ 18 \\ 24 \end{array})$
Der Normalenvektor kann noch um den Faktor $6$ verkürzt werden.
$\Rightarrow \vec{n} = (\begin{array}{c} 2 \\ 3 \\ 4 \end{array})$
Setze in die Normalenform ein:
$E : (\vec{X} - \vec{A}) \circ \vec{n}$ $=$ $0$
↓
Setze die Vektoren $\vec{A}$ und $\vec{n}$ ein.
$E_{A B C} : (\vec{X} - (\begin{array}{c} 6 \\ 0 \\ 3 \end{array})) \circ (\begin{array}{c} 2 \\ 3 \\ 4 \end{array})$ $=$ $0$
Schritt 2: Umwandlung in die Koordinatenform
$E_{A B C} : (\vec{X} - (\begin{array}{c} 6 \\ 0 \\ 3 \end{array})) \circ (\begin{array}{c} 2 \\ 3 \\ 4 \end{array}) = 0$
Berechne das Skalarprodukt:
$2 \cdot x_{1} + 3 \cdot x_{2} + 4 \cdot x_{3} - (6 \cdot 2 + 0 \cdot 3 + 3 \cdot 4) = 0$
$\Rightarrow E_{A B C} : 2 \cdot x_{1} + 3 \cdot x_{2} + 4 \cdot x_{3} - 24 = 0$
Antwort: Die Gleichung der Ebene $E_{A B C}$ in Koordinatenform lautet:
$E_{A B C} : 2 \cdot x_{1} + 3 \cdot x_{2} + 4 \cdot x_{3} - 24 = 0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Gleichung einer Geraden $h$ , die die Ebene $E_{A B C}$ senkrecht schneidet (Lotgerade).

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Ein Punkt der Ebene $E_{A B C}$ ist der Punkt $A$ . Ein zur Ebene senkrechter Vektor ist der Normalenvektor $\vec{n}$ .
Verwende für die Geradengleichung den Punkt $A$ als Aufpunkt und den Vektor $\vec{n}$ als Richtungsvektor.
Antwort: Die Gleichung einer Geraden $h$ , die die Ebene $E_{A B C}$ senkrecht schneidet, lautet:
$h : \vec{X} = (\begin{array}{c} 6 \\ 0 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 3 \\ 4 \end{array})$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

6
Gegeben sind die Eckpunkte einer Pyramide $A (0 | 0 | 0)$ , $B (6 | 0 | 0)$ , $C (6 | 6 | 0)$ , $D (0 | 6 | 0)$ , $S (3 | 3 | 12)$ und die Gleichung einer Ebene $K : 2 x_{2} + 4,5 x_{3} = 20$ . Die Pyramide wird von der Ebene $K$ geschnitten.
1. Zeige, dass die Schnittfläche zwischen Pyramide und Ebene ein gleichschenkliges (symmetrisches) Trapez ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Die folgende Skizze (nicht maßstabsgetreu) verdeutlicht die Aufgabenstellung und dient zur Orientierung bei der Benennung der Pyramidenpunkte.
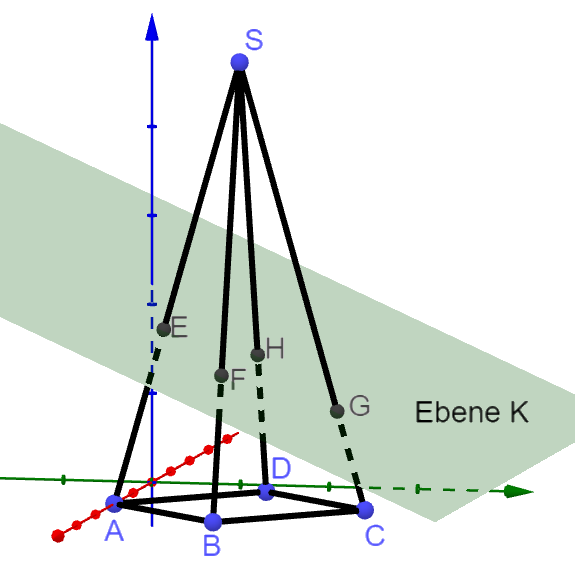
  Berechne die Gleichungen der Pyramidenkanten
  $g_{A S} : \vec{X} = \vec{A} + r \cdot (\vec{S} - \vec{A}) = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 0 \\ 3 - 0 \\ 12 - 0 \end{array})$
  Kürze den Richtungsvektor mit Faktor $3$ :
  $g_{A S} : \vec{X} = r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
  $g_{B S} : \vec{X} = \vec{B} + r \cdot (\vec{S} - \vec{B}) = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 6 \\ 3 - 0 \\ 12 - 0 \end{array})$
  Kürze den Richtungsvektor mit Faktor $3$ :
  $g_{B S} : \vec{X} = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
  $g_{C S} : \vec{X} = \vec{C} + r \cdot (\vec{S} - \vec{C}) = (\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 6 \\ 3 - 6 \\ 12 - 0 \end{array})$
  Kürze den Richtungsvektor mit Faktor $3$ :
  $g_{C S} : \vec{X} = (\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
  $g_{D S} : \vec{X} = \vec{D} + r \cdot (\vec{S} - \vec{D}) = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 3 - 0 \\ 3 - 6 \\ 12 - 0 \end{array})$
  Kürze den Richtungsvektor mit Faktor $3$ :
  $g_{D S} : \vec{X} = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
  Schneide die Geraden jeweils mit der Ebene $K$
  $g_{A S} \cap K$ :
  $g_{A S} : \vec{X} = r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
  $K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
  ↓
  Setze $x_{2} = r$ und $x_{3} = 4 r$ ein.
  $2 \cdot r + 4,5 \cdot 4 r$ $=$ $20$
  $2 r + 18 r$ $=$ $20$
  $20 r$ $=$ $20$ $: 20$
  $r$ $=$ $1$
  Setze $r = 1$ in $g_{A S}$ ein, um die Koordinaten $E$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
  $\vec{X}$ $=$ $r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
  ↓
  Setze $r = 1$ ein.
  $=$ $1 \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
  ↓
  Vereinfache.
  $=$ $(\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
  Damit hat der Punkt $E$ die Koordinaten $E (1 | 1 | 4)$ .
  $g_{B S} \cap K$ :
  $g_{B S} : \vec{X} = (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
  $K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
  ↓
  Setze $x_{2} = r$ und $x_{3} = 4 r$ ein.
  $2 \cdot r + 4,5 \cdot 4 r$ $=$ $20$
  $2 r + 18 r$ $=$ $20$
  $20 r$ $=$ $20$ $: 20$
  $r$ $=$ $1$
  Setze $r = 1$ in $g_{B S}$ ein, um die Koordinaten $F$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
  $\vec{X}$ $=$ $(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
  ↓
  Setze $r = 1$ ein.
  $=$ $(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
  ↓
  Vereinfache.
  $=$ $(\begin{array}{c} 5 \\ 1 \\ 4 \end{array})$
  Damit hat der Punkt $F$ die Koordinaten $F (5 | 1 | 4)$ .
  $g_{C S} \cap K :$
  $g_{C S} : \vec{X} = (\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
  $K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
  ↓
  Setze $x_{2} = 6 - r$ und $x_{3} = 4 r$ ein.
  $2 \cdot (6 - r) + 4,5 \cdot 4 r$ $=$ $20$
  $12 - 2 r + 18 r$ $=$ $20$
  $12 + 16 r$ $=$ $20$ $- 12$
  $16 r$ $=$ $8$ $: 16$
  $r$ $=$ $0,5$
  Setze $r = 0,5$ in $g_{C S}$ ein, um die Koordinaten $G$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
  $\vec{X}$ $=$ $(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
  ↓
  Setze $r = 0,5$ ein.
  $=$ $(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
  ↓
  Vereinfache.
  $=$ $(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$
  Damit hat der Punkt $G$ die Koordinaten $G (5,5 | 5,5 | 2)$ .
  $g_{D S} \cap K :$
  $g_{D S} : \vec{X} = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
  $K : 2 x_{2} + 4,5 x_{3}$ $=$ $20$
  ↓
  Setze $x_{2} = 6 - r$ und $x_{3} = 4 r$ ein.
  $2 \cdot (6 - r) + 4,5 \cdot 4 r$ $=$ $20$
  $12 - 2 r + 18 r$ $=$ $20$
  $12 + 16 r$ $=$ $20$ $- 12$
  $16 r$ $=$ $8$ $: 16$
  $r$ $=$ $0,5$
  Setze $r = 0,5$ in $g_{D S}$ ein, um die Koordinaten $H$ des Schnittpunktes mit der Ebene $K$ zu erhalten:
  $\vec{X}$ $=$ $(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
  ↓
  Setze $r = 0,5$ ein.
  $=$ $(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
  ↓
  Vereinfache.
  $=$ $(\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
  Damit hat der Punkt $H$ die Koordinaten $H (0,5 | 5,5 | 2)$ .
  Die Schnittfläche
  Die Punkte $E$ und $F$ haben die gleiche $x_{3}$ -Koordinate $4$ und die Punkte $G$ und $H$ haben die gleiche $x_{3}$ -Koordinate $2$ .
  Berechne die Vektoren $\vec{E F} = \vec{F} - \vec{E}$ und $\vec{H G} = \vec{G} - \vec{H} :$
  $\vec{E F}$ $=$ $(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
  $=$ $(\begin{array}{c} 4 \\ 0 \\ 0 \end{array})$
  $\vec{H G}$ $=$ $(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
  $=$ $(\begin{array}{c} 5 \\ 0 \\ 0 \end{array})$
  Damit folgt: $\vec{E F} ∥ \vec{H G}$
  Die beiden Vektoren sind ungleich lang:
  $| \vec{E F} | = \sqrt{4^{2} + 0^{2} + 0^{2}} = \sqrt{16} = 4$
  $| \vec{H G} | = \sqrt{5^{2} + 0^{2} + 0^{2}} = \sqrt{25} = 5$
  Berechne die Vektoren $\vec{G F} = \vec{F} - \vec{G}$ und $\vec{H E} = \vec{E} - \vec{H}$ :
  $\vec{G F}$ $=$ $(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$
  $=$ $(\begin{array}{c} - 0,5 \\ - 4,5 \\ 2 \end{array})$
  $\vec{H E}$ $=$ $(\begin{array}{c} 1 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
  $=$ $(\begin{array}{c} 0,5 \\ - 4,5 \\ 2 \end{array})$
  Die Vektoren sind nicht parallel zueinander:
  $(\begin{array}{c} - 0,5 \\ - 4,5 \\ 2 \end{array})$ $\neq$ $k \cdot (\begin{array}{c} 0,5 \\ - 4,5 \\ 2 \end{array})$
  Aber die beiden Vektoren sind gleich lang:
  $| \vec{G F} | = \sqrt{(- 0,5)^{2} + (- 4,5)^{2} + 2^{2}} = \sqrt{24,5}$
  $| \vec{H E} | = \sqrt{(0,5)^{2} + (- 4,5)^{2} + 2^{2}} = \sqrt{24,5}$
  Somit haben wir zwei ungleich lange parallele Vektoren $\vec{E F}$ und $\vec{H G}$ und zwei gleich lange, aber nicht parallele Vektoren $\vec{G F}$ und $\vec{H E}$ .
  Die geometrische Figur kann demnach nur ein gleichschenkeliges (symmetrisches) Trapez und kein Parallelogramm sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle die Geradengleichungen für die vier Pyramidenkanten und schneide sie jeweils mit der Ebene $K$ , um die Eckpunkte der Schnittfläche zu erhalten.
2. Berechne den Flächeninhalt des Trapezes.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Für die Trapezfläche gilt:
  $A_{Trapez} = \frac{a + c}{2} \cdot h$
  Die Längen der beiden parallelen Seiten wurden in Aufgabe a) berechnet:
  $a = | \vec{H G} | = 5$ und $c = | \vec{E F} | = 4$
  Die Länge der Seite $| \vec{G F} | = \sqrt{24,5}$ .
  Die Höhe des Trapezes muss noch berechnet werden:
  Die Höhe $h$ kann mit dem Satz des Pythagoras berechnet werden.
  Dazu muss erst die Länge der Seite x berechnet werden:
  $x = 0,5 \cdot (5 - 4) = 0,5$
  Dann gilt:
  $h = \sqrt{| \vec{G F} |^{2} - x^{2}}$
  $h = \sqrt{(\sqrt{24,5})^{2} - {0,5}^{2}}$
  $h = \sqrt{24,25} \approx 4,925$
  $A_{Trapez}$ $=$ $\frac{a + c}{2} \cdot h$
  ↓
  Setze $a = 5$ , $c = 4$ und $h = 4,925$ ein.
  $=$ $\frac{5 + 4}{2} \cdot 4,925$
  $\approx$ $22,16$
  Der Flächeninhalt des Trapezes beträgt etwa $22,16 FE$ .
  Die folgende Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung.
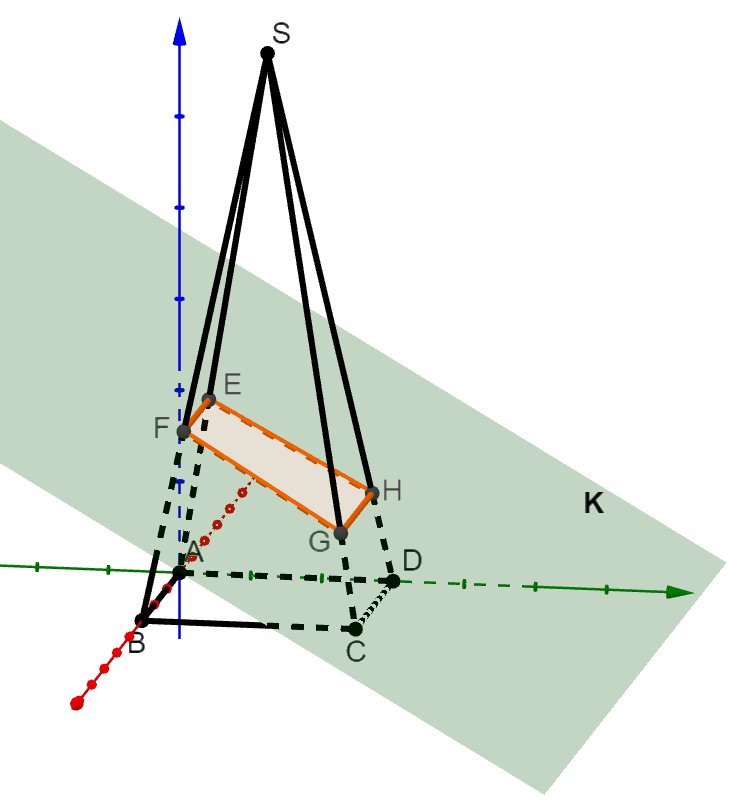
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\vec{X}$	$=$	$(\begin{array}{c} 6 \\ 0 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array})$
	↓	Setze für $\vec{X}$ den Vektor $\vec{C}$ ein.
$(\begin{array}{c} 0 \\ 6 \\ 1,5 \end{array})$	$=$	$(\begin{array}{c} 6 \\ 0 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array})$	$- (\begin{array}{c} 6 \\ 0 \\ 3 \end{array})$
	↓	Löse nach $r$ auf.
$(\begin{array}{c} 0 \\ 6 \\ 1,5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 3 \end{array})$	$=$	$r \cdot (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array})$
	↓	Fasse die linke Seite zusammen.
$(\begin{array}{c} - 6 \\ 6 \\ - 1,5 \end{array})$	$=$	$r \cdot (\begin{array}{c} 0 \\ 4 \\ - 3 \end{array})$

$E : (\vec{X} - \vec{A}) \circ \vec{n}$	$=$	$0$
	↓	Setze die Vektoren $\vec{A}$ und $\vec{n}$ ein.
$E_{A B C} : (\vec{X} - (\begin{array}{c} 6 \\ 0 \\ 3 \end{array})) \circ (\begin{array}{c} 2 \\ 3 \\ 4 \end{array})$	$=$	$0$

$K : 2 x_{2} + 4,5 x_{3}$	$=$	$20$
	↓	Setze $x_{2} = r$ und $x_{3} = 4 r$ ein.
$2 \cdot r + 4,5 \cdot 4 r$	$=$	$20$
$2 r + 18 r$	$=$	$20$
$20 r$	$=$	$20$	$: 20$
$r$	$=$	$1$

$\vec{X}$	$=$	$r \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
	↓	Setze $r = 1$ ein.
	$=$	$1 \cdot (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$

$\vec{X}$	$=$	$(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
	↓	Setze $r = 1$ ein.
	$=$	$(\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) + 1 \cdot (\begin{array}{c} - 1 \\ 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 5 \\ 1 \\ 4 \end{array})$

$K : 2 x_{2} + 4,5 x_{3}$	$=$	$20$
	↓	Setze $x_{2} = 6 - r$ und $x_{3} = 4 r$ ein.
$2 \cdot (6 - r) + 4,5 \cdot 4 r$	$=$	$20$
$12 - 2 r + 18 r$	$=$	$20$
$12 + 16 r$	$=$	$20$	$- 12$
$16 r$	$=$	$8$	$: 16$
$r$	$=$	$0,5$

$\vec{X}$	$=$	$(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
	↓	Setze $r = 0,5$ ein.
	$=$	$(\begin{array}{c} 6 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} - 1 \\ - 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$

$\vec{X}$	$=$	$(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
	↓	Setze $r = 0,5$ ein.
	$=$	$(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} 1 \\ - 1 \\ 4 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$

$\vec{E F}$	$=$	$(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 4 \end{array})$
	$=$	$(\begin{array}{c} 4 \\ 0 \\ 0 \end{array})$

$\vec{H G}$	$=$	$(\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
	$=$	$(\begin{array}{c} 5 \\ 0 \\ 0 \end{array})$

$\vec{G F}$	$=$	$(\begin{array}{c} 5 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 5,5 \\ 5,5 \\ 2 \end{array})$
	$=$	$(\begin{array}{c} - 0,5 \\ - 4,5 \\ 2 \end{array})$

$A_{Trapez}$	$=$	$\frac{a + c}{2} \cdot h$
	↓	Setze $a = 5$ , $c = 4$ und $h = 4,925$ ein.
	$=$	$\frac{5 + 4}{2} \cdot 4,925$
	$\approx$	$22,16$

$\vec{H E}$	$=$	$(\begin{array}{c} 1 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 0,5 \\ 5,5 \\ 2 \end{array})$
	$=$	$(\begin{array}{c} 0,5 \\ - 4,5 \\ 2 \end{array})$

Gemischte Aufgaben

Spurpunkt in der x1x2​-Ebene

Spurpunkt in der x1x3​-Ebene

Spurpunkt in der x2x3​-Ebene

Hast du eine Frage oder Feedback?

Spurpunkt in der x1x2​-Ebene

Spurpunkt in der x1x3​-Ebene

Spurpunkt in der x2x3​-Ebene

Hast du eine Frage oder Feedback?

Spurpunkt in der x1x2​-Ebene

Spurpunkt in der x1x3​-Ebene

Spurpunkt in der x2x3​-Ebene

Hast du eine Frage oder Feedback?

Spurpunkt in der x1x2​-Ebene

Spurpunkt in der x1x3​-Ebene

Spurpunkt in der x2x3​-Ebene

Hast du eine Frage oder Feedback?

Spurpunkt in der x1x2​-Ebene

Spurpunkt in der x1x3​-Ebene

Spurpunkt in der x2x3​-Ebene

Hast du eine Frage oder Feedback?

Spurpunkt in der x1x2​-Ebene

Spurpunkt in der x1x3​-Ebene

Spurpunkt in der x2x3​-Ebene

Hast du eine Frage oder Feedback?

Länge der Strecken

Umfang des Dreiecks

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Der zu berechnende Term

Länge der Wege berechnen

Wege verkürzen

Vektorkette bilden

Hast du eine Frage oder Feedback?

Schwierigkeit der Route

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Schritt 1: Umwandlung in die Normalenform

Schritt 2: Umwandlung in die Koordinatenform

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechne die Gleichungen der Pyramidenkanten

Schneide die Geraden jeweils mit der Ebene K

Die Schnittfläche

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Spurpunkt in der $x_{1} x_{2}$ -Ebene

Spurpunkt in der $x_{1} x_{3}$ -Ebene

Spurpunkt in der $x_{2} x_{3}$ -Ebene

Spurpunkt in der $x_{1} x_{2}$ -Ebene

Spurpunkt in der $x_{1} x_{3}$ -Ebene

Spurpunkt in der $x_{2} x_{3}$ -Ebene

Spurpunkt in der $x_{1} x_{2}$ -Ebene

Spurpunkt in der $x_{1} x_{3}$ -Ebene

Spurpunkt in der $x_{2} x_{3}$ -Ebene

Spurpunkt in der $x_{1} x_{2}$ -Ebene

Spurpunkt in der $x_{1} x_{3}$ -Ebene

Spurpunkt in der $x_{2} x_{3}$ -Ebene

Spurpunkt in der $x_{1} x_{2}$ -Ebene

Spurpunkt in der $x_{1} x_{3}$ -Ebene

Spurpunkt in der $x_{2} x_{3}$ -Ebene

Spurpunkt in der $x_{1} x_{2}$ -Ebene

Spurpunkt in der $x_{1} x_{3}$ -Ebene

Spurpunkt in der $x_{2} x_{3}$ -Ebene

Schneide die Geraden jeweils mit der Ebene $K$