🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Hessesche Normalenform

Die Hessesche Normalenform ist eine spezielle Form einer Ebenengleichung.

Sie ist nach dem deutschen Mathematiker Ludwig Otto Hesse (1811-1874) benannt.

Mithilfe der Hesseschen Normalenform kann

  • der Abstand eines Punktes von einer Ebene berechnet werden,

  • kann man eine Aussage über die Lage eines Punktes bzgl. einer Ebene erhalten.

Hesse Ebene mit Einheitsvektor

Abbildung 1

Die Gleichung der Hesseschen Normalenform

MerkeHessesche Normalenform

Die Hessesche Normalenform ist eine spezielle Form der Normalenform.

Eine Ebenengleichung heißt dann Hessesche Normalenform, wenn ...

  1. ... der Normalenvektor normiert ist, d.h. ∣n⃗0∣=1\left|\vec{n}_0\right|=1 mit n⃗0=n⃗∣n⃗∣\vec n_0=\dfrac{\vec n}{|\vec n|}

  2. ... die Richtung von n⃗0\vec{n}_0 so gewählt ist, dass P⃗∘n⃗0≥0\vec{P}\circ\vec{n}_0\ge0 ist. Dann zeigt n⃗0 \vec{n}_0 vom Koordinatenursprung in Richtung der Ebene (d.h. in den Halbraum, in dem O O nicht liegt). P⃗\vec P ist der Ortsvektor eines Ebenenpunktes.

Dann ist die Hessesche Normalenform:

n⃗0∘(X⃗−P⃗)=0        \displaystyle \vec{n}_0\circ\left(\vec{X}-\vec{P}\right)=0\;\;\;\;
BeachteHessesche Normalenform im R2\displaystyle \mathbb {R} ^{2}

Die Hessesche Normalenform kann auch für Geraden (im R2\displaystyle \mathbb {R} ^{2}) erstellt werden.

In diesem Fall kann die Hessesche Normalenform zur Abstandberechnung eines Punktes von einer Geraden verwendet werden.

Wie erstellt man die Hessesche Normalenform?

Der Normalenvektor n⃗\vec n muss normiert werden. Dazu wird der Vektor n⃗\vec n durch seinen Betrag geteilt und man erhält den Normaleneinheitsvektor n⃗0\vec{n}_0   ⇒  n⃗0=n⃗∣n⃗∣\;\Rightarrow\;\vec{n}_0=\dfrac {\vec n}{\left|\vec n\right|}

Man prüft nun, ob P⃗∘n⃗0≥0\vec{P}\circ\vec{n}_0\ge0 ist. Ist das nicht der Fall, muss die Richtung des Normaleneinheitsvektors umgedreht werden. Dazu multipliziert man den Normaleneinheitsvektor mit (−1) (-1).

Dann ist die Hessesche Normalenform:

EHNF:  n⃗∣n⃗∣∘(X→−P→)=0\displaystyle E_{\text{HNF}}: \;\dfrac{\vec n}{|\vec n|} \circ\left(\overrightarrow{X}-\overrightarrow{P}\right)=0

oder

EHNF:  n⃗0∘(X→−P→)=0\displaystyle E_{\text{HNF}}: \;\vec n_0 \circ\left(\overrightarrow{X}-\overrightarrow{P}\right)=0
BeispielUmwandlung einer Ebene EE in die Hessesche Normalenform

Erstelle die Hessesche Normalenform der Ebene E:  (122)∘[X→−(103)]=0E:\;\begin{pmatrix}1\\2\\2\end{pmatrix}\circ\left[\overrightarrow{X}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]=0

Lösung:

Lies aus der Ebenengleichung den Normalenvektor ab.

n⃗=(122)\vec n=\begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}

Berechne den Betrag des Normalenvektors.

∣n⃗∣\displaystyle |\vec{n}|==12+22+22\displaystyle \sqrt{1^2+2^2+2^2}
↓

Berechne die Quadrate.

==9\displaystyle \sqrt{9}
↓

Berechne die Wurzel.

==3\displaystyle 3

Berechne den Normaleneinheitsvektor

n⃗0\displaystyle \vec{n}_0==n⃗∣n⃗∣\displaystyle \dfrac{\vec{n}}{|\vec{n}|}
↓

Teile den Vektor n⃗\vec n durch seinen Betrag 33.

n⃗0\displaystyle \vec{n}_0==13⋅(122)\displaystyle \dfrac{1}{3}\cdot\begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}
↓

Multipliziere.

n⃗0\displaystyle \vec{n}_0==(132323)\displaystyle \begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}

Ersetze den Normalenvektor n⃗\vec n in der Ebenengleichung EE durch den Normaleneinheitsvektor n⃗0\vec{n}_0.

EHNF:  (132323)∘[X→−(103)]=0\displaystyle E_{\text{HNF}}: \;\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\left[\overrightarrow{X}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]=0

Es muss noch die Richtung des Vektors n⃗0 \vec{n}_0 überprüft werden.

Dabei muss gelten: P⃗∘n⃗0≥0\vec{P}\circ\vec{n}_0\ge0

P⃗∘n⃗0\displaystyle \vec{P}\circ\vec{n}_0≥≥0\displaystyle 0
↓

Setze P⃗=(103) \vec P=\begin{pmatrix}1\\0\\3\end{pmatrix} und n0⃗=(132323)\vec{n_0} = \begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}ein.

(103)∘(132323)\displaystyle \begin{pmatrix}1\\[1ex]0\\[1ex]3\end{pmatrix}\circ\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}≥≥0\displaystyle 0
↓

Berechne das Skalarprodukt.

1⋅13+0⋅23+3⋅23\displaystyle 1\cdot\dfrac{1}{3}+0\cdot\dfrac{2}{3}+3\cdot\dfrac{2}{3}≥≥0\displaystyle 0
↓

Fasse zusammen.

13+63\displaystyle \dfrac{1}{3}+\dfrac{6}{3}≥≥0\displaystyle 0
73\displaystyle \dfrac{7}{3}≥≥0  ✓\displaystyle 0\;\checkmark

Damit hat der Normaleneinheitsvektor die für die Hessesche Normalenform passende Richtung.

Dann ist die Hessesche Normalenform:

\displaystyle
EHNF:  (132323)∘[X→−(103)]=0\displaystyle E_{\text{HNF}}:\;\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\left[\overrightarrow{X}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]=0

Abstandsberechnungen

Abstand der Ebene EE vom Koordinatenursprung OO

MerkeAbstand der Ebene EE vom Ursprung

Es wird vorausgesetzt, dass P⃗∘n⃗0≥0\vec{P}\circ\vec{n}_0\ge0 ist, dann gilt für den Abstand dd der Ebene EE vom Koordinatenursprung OO die Formel:

d=P⃗∘n⃗0\displaystyle d=\vec{P}\circ\vec{n}_0
BeispielAbstand der Ebene EE vom Ursprung

Gegeben ist die Hessesche Normalenform:

EHNF:  (132323)∘[X→−(103)]=0E_{\text{HNF}}:\;\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\left[\overrightarrow{X}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]=0

Welchen Abstand hat die Ebene vom Koordinatenursprung?

Lösung:

Man setzt in die Abstandsformel ein:

d=P⃗∘n⃗0d=\vec{P}\circ\vec{n}_0

Das Produkt P⃗∘n⃗0 \vec{P}\circ\vec{n}_0 wurde im Beispiel "Umwandlung einer Ebene EE in die Hessesche Normalenform" bereits berechnet:

P⃗∘n⃗0=73\vec{P}\circ\vec{n}_0=\dfrac{7}{3}

Damit ist d=73d=\dfrac{7}{3}.

Der Abstand der Ebene EE vom Koordinatenursprung beträgt 73  LE\dfrac{7}{3}\; \mathrm{LE}.

Abstand eines Punktes von der Ebene EE

Setzt man in den Term n⃗0∘(X→−P→)\vec{n}_0\circ\left(\overrightarrow{X}-\overrightarrow{P}\right) der Hesseschen Normalenform für den Vektor X⃗\vec X den Ortsvektor eines Punktes QQ ein, so erhält man eine Zahl.

Der Betrag dieser Zahl ist der Abstand des Punktes QQ von der Ebene E E.

MerkeAbstandsberechnung für einen Punkt QQ von der Ebene EE

Für den Abstand eines Punktes QQ von der Ebene E E gilt die Formel:

d(Q,E)=∣n⃗0∘(Q→−P→)∣\displaystyle d(Q,E)=\left|\vec{n}_0\circ\left(\overrightarrow{Q}-\overrightarrow{P}\right)\right|

Ist d(Q,E)=0d(Q,E)=0, dann liegt der Punkt QQ in der Ebene EE.

Hessesche Normalenform

Abbildung 2

BeispielAbstandsberechnung für einen Punkt QQ von der Ebene EE

Gegeben ist die Hessesche Normalenform EHNF:  (132323)∘[X→−(103)]=0E_{\text{HNF}}:\;\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\left[\overrightarrow{X}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]=0 und ein Punkt Q(2∣−4∣1)Q(2|-4|1). Berechne den Abstand des Punktes QQ von der Ebene.

Lösung:

Man setzt in die Abstandsformel ein:

d(Q,E)\displaystyle d(Q,E)==∣n⃗0∘(Q→−P→)∣\displaystyle \left|\vec{n}_0\circ\left(\overrightarrow{Q}-\overrightarrow{P}\right)\right|
↓

Setze n⃗0=(132323)\vec n_0=\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}, Q⃗=(2−41)\vec Q= \begin{pmatrix}2\\-4\\1\end{pmatrix} und P⃗=(103)\vec P= \begin{pmatrix}1\\0\\3\end{pmatrix} ein.

d(Q,E)\displaystyle d(Q,E)==∣(132323)∘[(2−41)−(103)]∣\displaystyle \left|\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\left[\begin{pmatrix}2\\-4\\1\end{pmatrix}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]\right|
↓

Berechne die Differenz.

==∣(132323)∘(1−4−2)∣\displaystyle \left|\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\begin{pmatrix}1\\-4\\-2\end{pmatrix}\right|
↓

Berechne das Skalarprodukt.

==∣(13⋅1+23⋅(−4)+23⋅(−2))∣\displaystyle \left|\left(\dfrac{1}{3}\cdot 1+\dfrac{2}{3}\cdot(-4)+\dfrac{2}{3}\cdot(-2)\right)\right|
==∣13−83−43∣\displaystyle \left|\dfrac{1}{3}-\dfrac{8}{3}-\dfrac{4}{3}\right|
==∣−113∣\displaystyle \left|-\dfrac{11}{3}\right|
==113\displaystyle \dfrac{11}{3}

Der Abstand des Punktes QQ von der Ebene EE beträgt 113  LE \dfrac{11}{3}\; \mathrm{LE}.

Lage eines Punktes QQ bezüglich einer Ebene EE

Der Ortsvektor des gegebenen Punktes QQ wird in den Term n⃗0∘(X→−P→)\vec{n}_0\circ \left(\overrightarrow{X}-\overrightarrow{P}\right) der Hesseschen Normalenform für den Vektor X⃗\vec X eingesetzt und man erhält eine Zahl.

  • Die Zahl ist positiv, dann liegt QQ in dem Halbraum, in dem O O nicht liegt (siehe Abbildung 22)

  • Die Zahl ist negativ, dann liegt QQ in dem Halbraum in dem O O liegt (siehe Abbildung 33)

  • Die Zahl ist null, dann liegt QQ in der Ebene EE

BeispielLage eines Punktes QQ bezüglich einer Ebene EE

Gegeben ist die Hessesche Normalenform EHNF:  (132323)∘[X→−(103)]=0E_{\text{HNF}}:\;\begin{pmatrix}\frac{1}{3}\\[1ex]\frac{2}{3}\\[1ex]\frac{2}{3}\end{pmatrix}\circ\left[\overrightarrow{X}-\begin{pmatrix}1\\0\\3\end{pmatrix}\right]=0 und ein Punkt Q(2∣−4∣1)Q(2|-4|1). Welche Lage hat QQ bezüglich der Ebene EE?

Lösung:

Die im Beispiel "Abstandsberechnung für einen Punkt QQ von der Ebene EE" berechnete Zahl war −113-\dfrac{11}{3}, d.h. negativ. Damit liegt QQ auf der gleichen Seite wie der Koordinatenursprung.

Graphische Darstellung

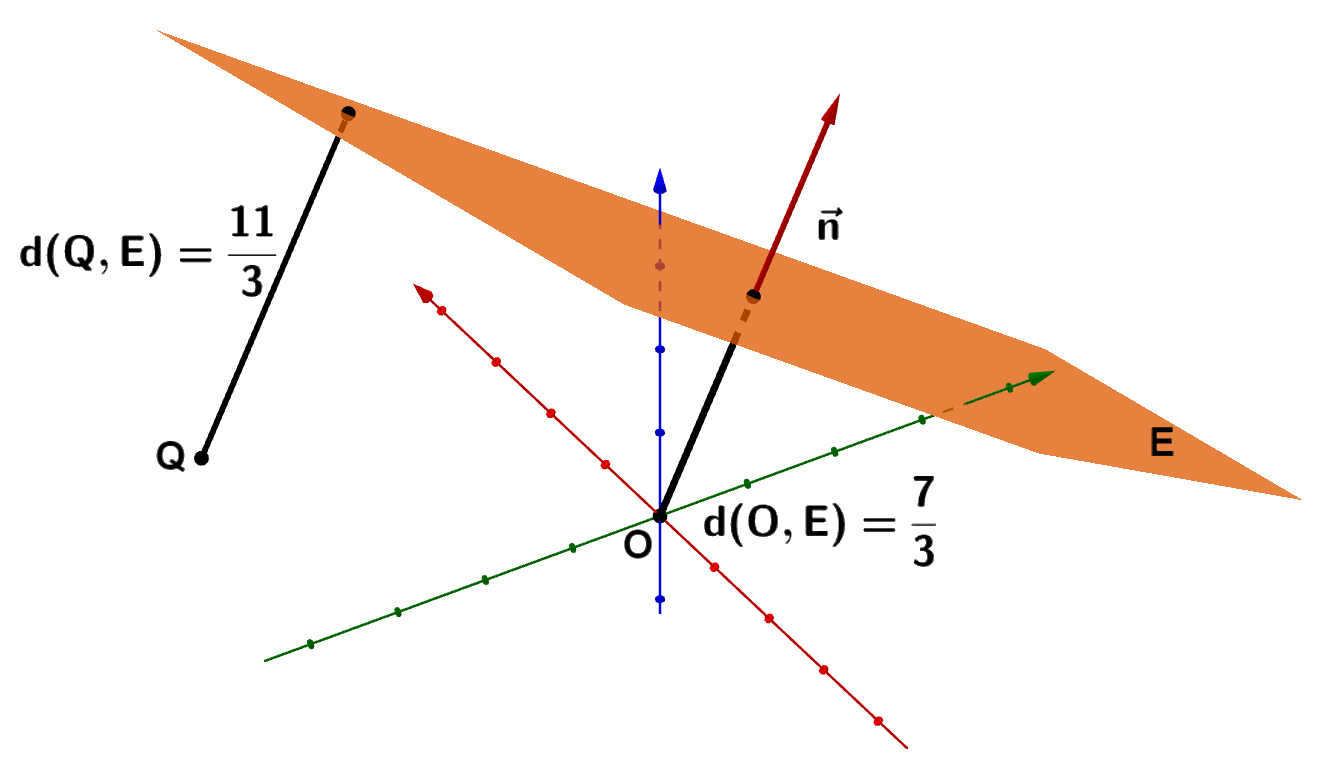
Punkt und Ebene

Abbildung 3: Q liegt auf der gleichen Seite wie der Koordinatenursprung


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?