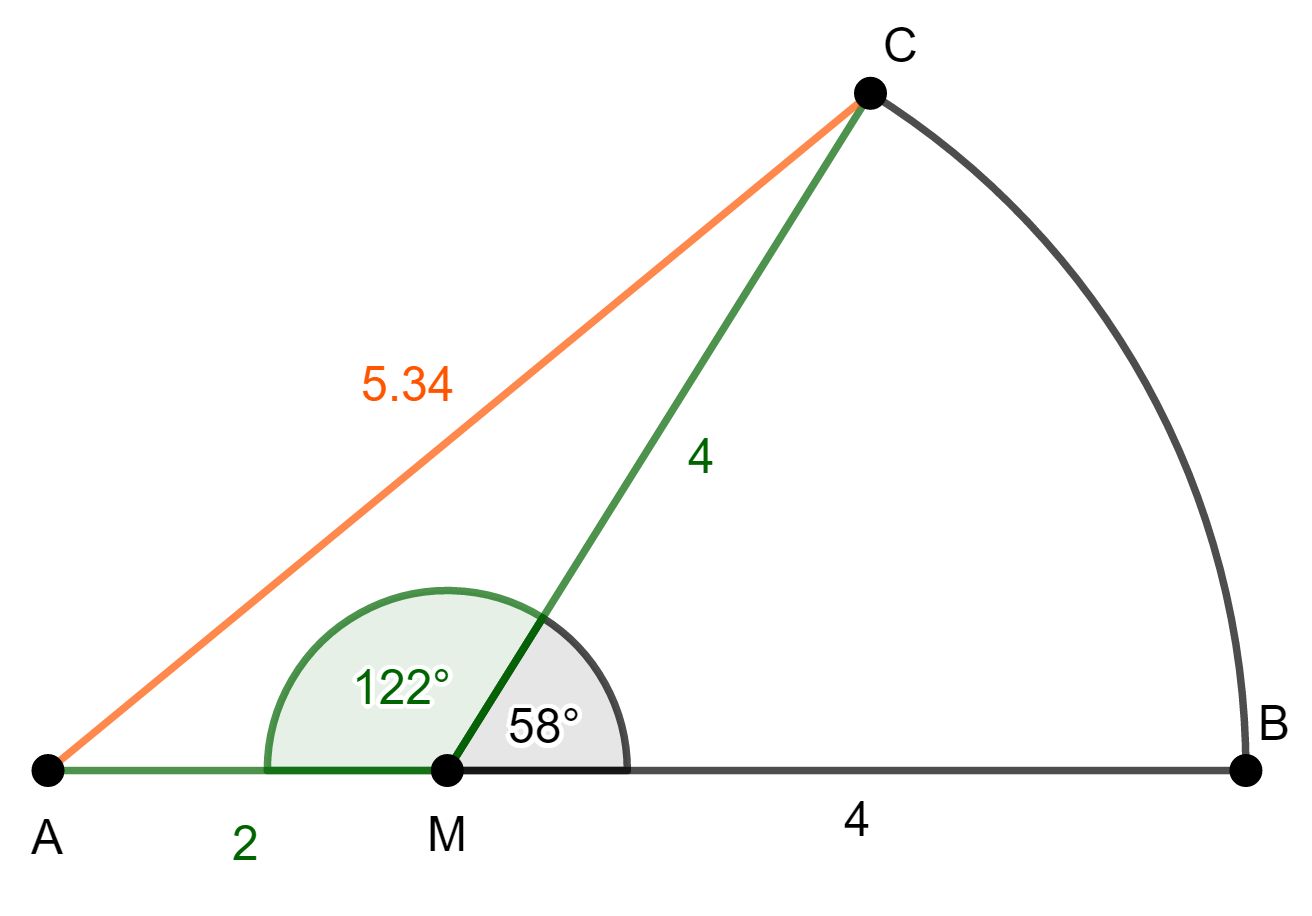
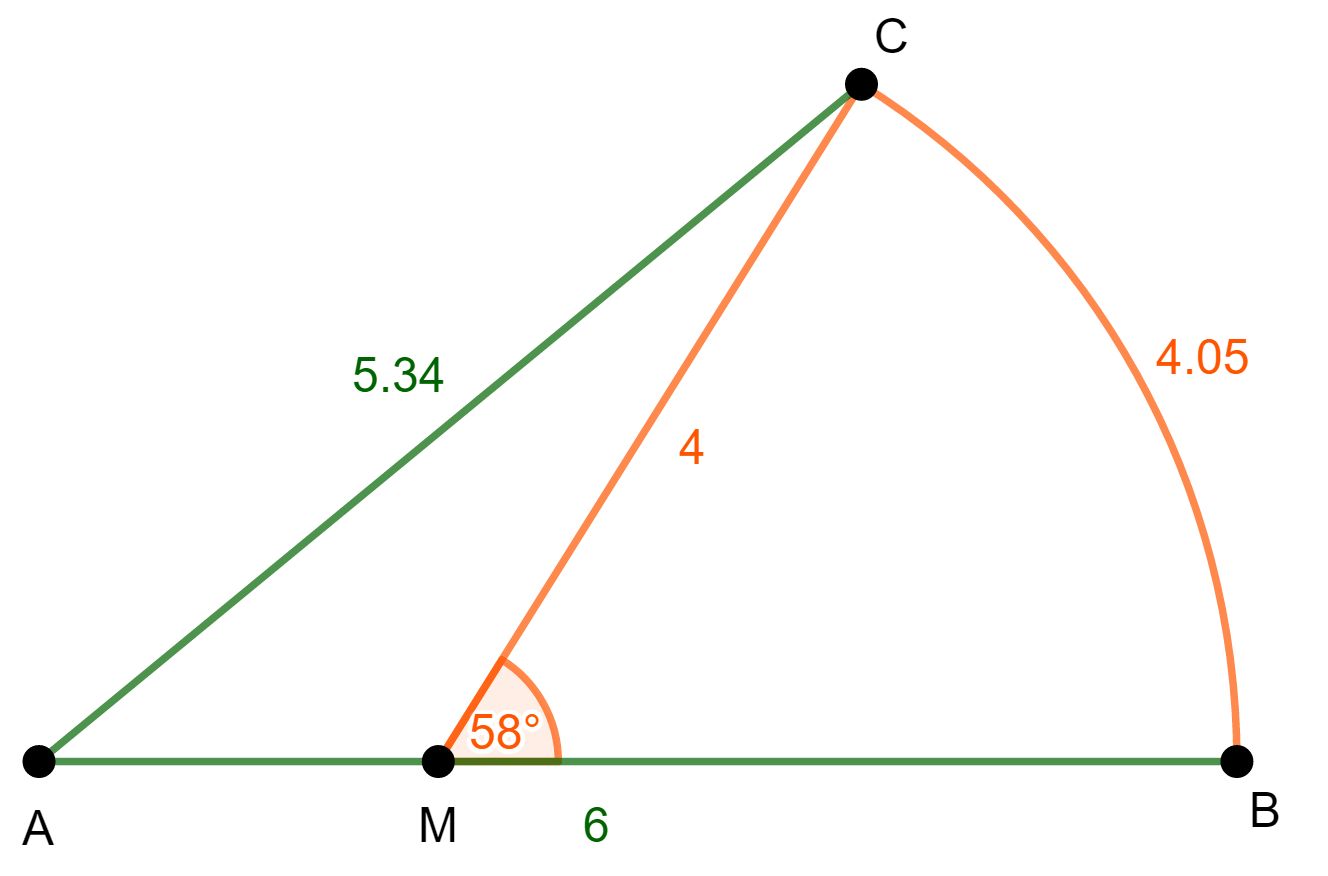
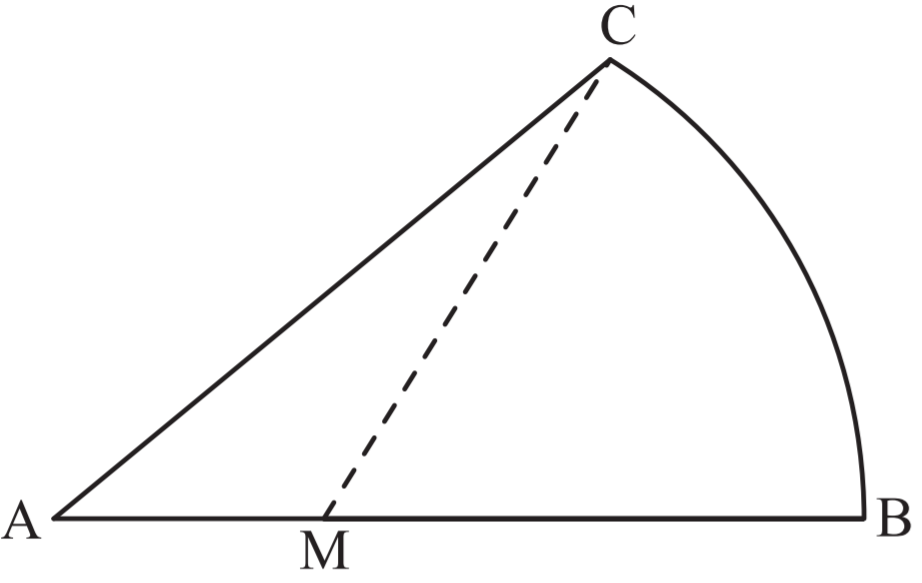
Die nebenstehende Figur ist durch den Kreisbogen mit dem Radius und die Strecken und begrenzt.
Es gilt: .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Bestimmen Sie rechnerisch das Maß des Winkels .
[Teilergebnis: ]
Berechnen Sie den Umfang der Figur.