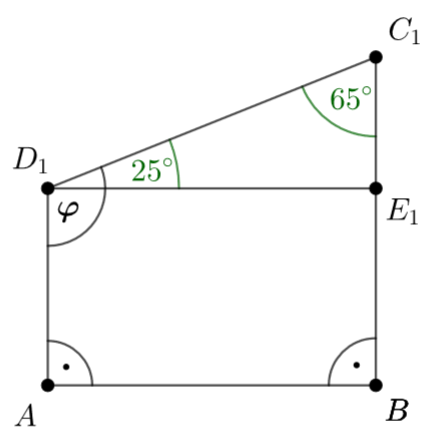
Für Trapeze mit den parallelen Seiten und [] gilt:
; = 90°; .
Die Winkel haben das Maß mit ]90°; 180°[.
Die Zeichnung zeigt das Trapez für .
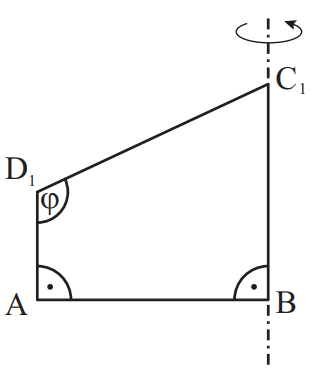
Zeigen Sie, dass für die Längen der Strecken und in Abhängigkeit von gilt:
und
Die Trapeze rotieren um die Gerade . Berechnen Sie für den Oberflächeninhalt des entstehenden Rotationskörpers.