Nachtermin Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zu ausdrucken.

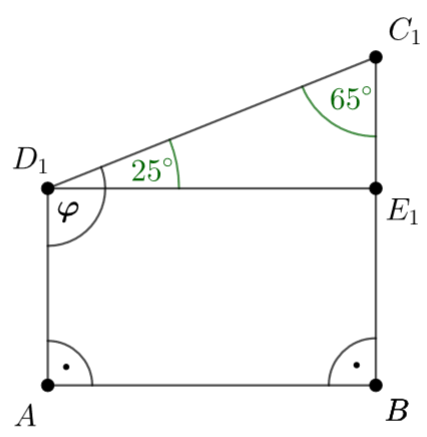
Für Trapeze $ABC_nD_n$ mit den parallelen Seiten $[AD_n]$ und [ $BC_n$ ] gilt:

$\overline{AB}=3cm$ ; $\measuredangle C_nBA$ = 90°; $\overline{BC}_n=2\cdot\overline{AD}_n$ .

Die Winkel $AD_nC_n$ haben das Maß $\varphi$ mit $\varphi\in\$ ]90°; 180°[.

Die Zeichnung zeigt das Trapez $ABC_1D_1$ für $\varphi=115°$ .

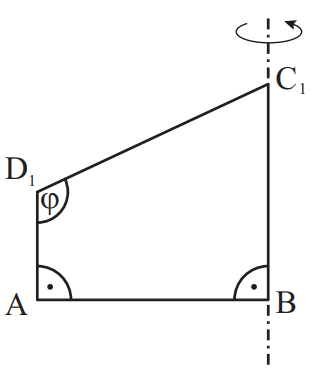
Zeigen Sie, dass für die Längen der Strecken $\left[C_nD_n\right]$ und $\left[AD_n\right]$ in Abhängigkeit von $\varphi$ gilt:
$\overline{C_nD_n}\left(\varphi\right)=\dfrac{3}{\cos\left(\varphi-90°\right)}cm$ und $\overline{AD_n}\left(\varphi\right)=3\cdot\tan\left(\varphi-90°\right)cm$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez, Kosinus und Tangens
Wir zeichnen die Strecken $\overline{D_nE}$ senkrecht zu den Strecken $\overline{BC_n}$ . Die Schnittpunkte sind $E_n$ . Die entstehenden Dreiecke $E_nD_nC_n$ sind rechtwinklig.
Die entstehenden Vierecke $AD_nE_nB$ sind Rechtecke und somit gilt $\overline{D_nE_n}=\overline{AB}=3$ cm. Dazu gilt $\overline{E_nB}=\overline{AD_n}$ , weil die Seite $\overline{BC_n}$ doppelt so lang ist, wie $\overline{AD_n}$ .
Seiten $\overline{C_nD_n}(\varphi)$
In den Dreiecken $E_nD_nC_n$ gilt:
$cos (\sphericalangle E_nD_nC_n)=\dfrac{\overline{E_nD_n}(\varphi)}{\overline{C_nD_n}(\varphi)}$
Wir ersetzen $\overline{E_nD_n}(\varphi)$ durch 3 und $\sphericalangle E_nD_nC_n$ durch $(\varphi - 90)$ :
$\cos(\varphi - 90))=\dfrac{3}{\overline{C_nD_n}(\varphi)}$ $\Rightarrow \overline{C_{n}D_{n}}(\varphi)=\dfrac{3}{\cos(\varphi - 90)}$
Seiten $\overline{AD_n}(\varphi)$
In den Dreiecken $E_nD_nC_n$ gilt auch:
$tan (\sphericalangle E_nD_nC_n)=\dfrac{\overline{E_nC_n}(\varphi)}{\overline{E_nD_n}(\varphi)}$
Wir ersetzen $\overline{E_nC_n}(\varphi)$ durch $\overline{AD_n}(\varphi)$ , $\overline{E_nD_n}(\varphi)$ durch 3, und $\sphericalangle E_nD_nC_n$ durch $(\varphi - 90)$ :
$tan (\varphi - 90)=\dfrac{\overline{AD_n}(\varphi)}{3}$ $\Rightarrow$ $\overline{AD_n}(\varphi)=3\cdot tan (\varphi - 90)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne eine Skizze der Aufgabe oder nutze die Skizze in der Aufgabenstellung.
Zeichne die Strecke $\overline{D_nE}$ senkrecht zu $\overline{BC_n}$ (das Lot).
In diesem rechtwinkligen Dreieck lassen sich $\overline{C_nD_n}(\varphi)$ und $\overline{AD_n}(\varphi)$ berechnen.
Der Winkel in diesem rechtwinkligen Dreieck lässt sich ausdrücken durch $(\varphi - 90)$ .

Die Trapeze $ABC_nD_n$ rotieren um die Gerade $BC_n$ . Berechnen Sie für den Oberflächeninhalt des entstehenden Rotationskörpers.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
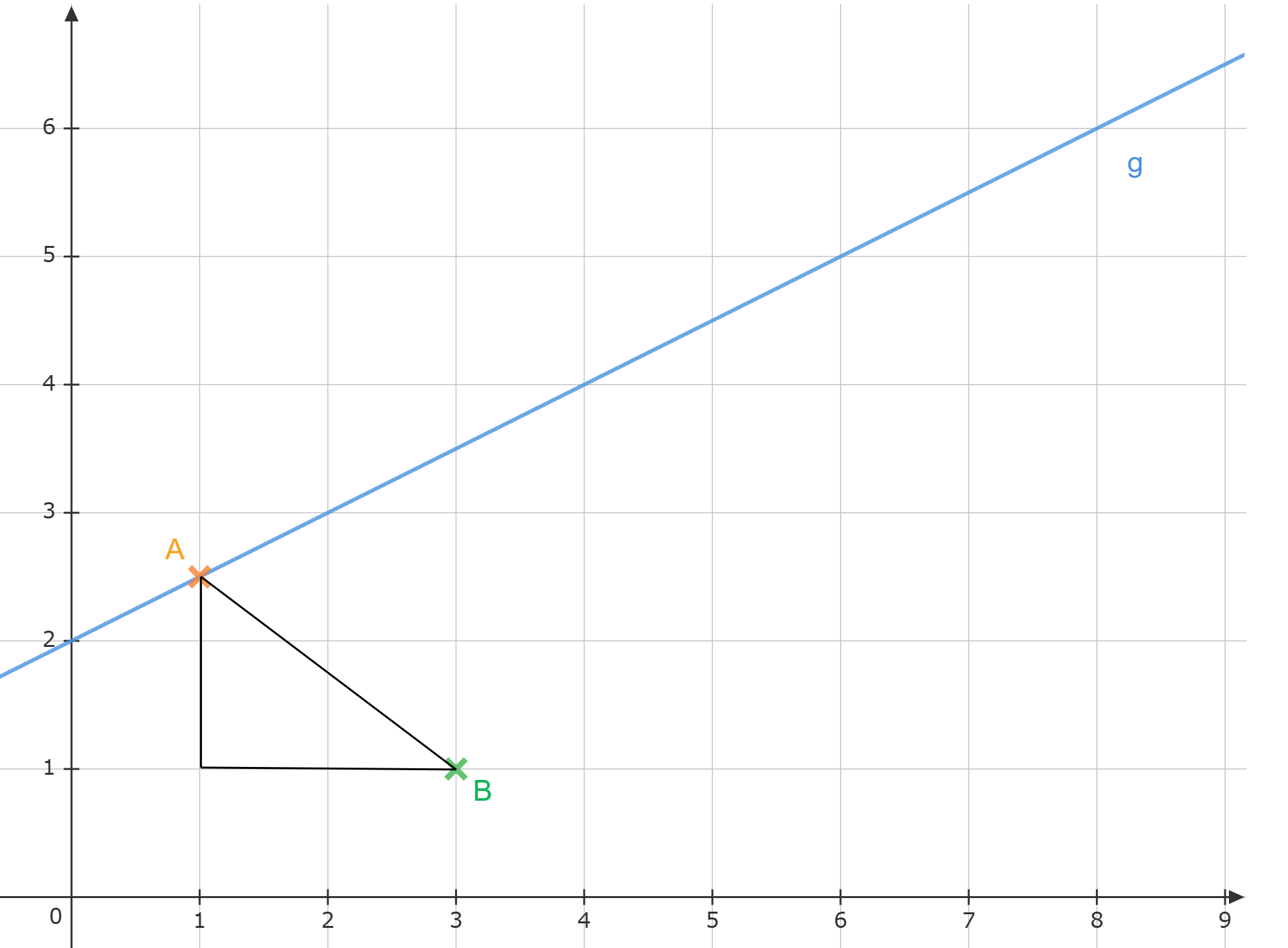
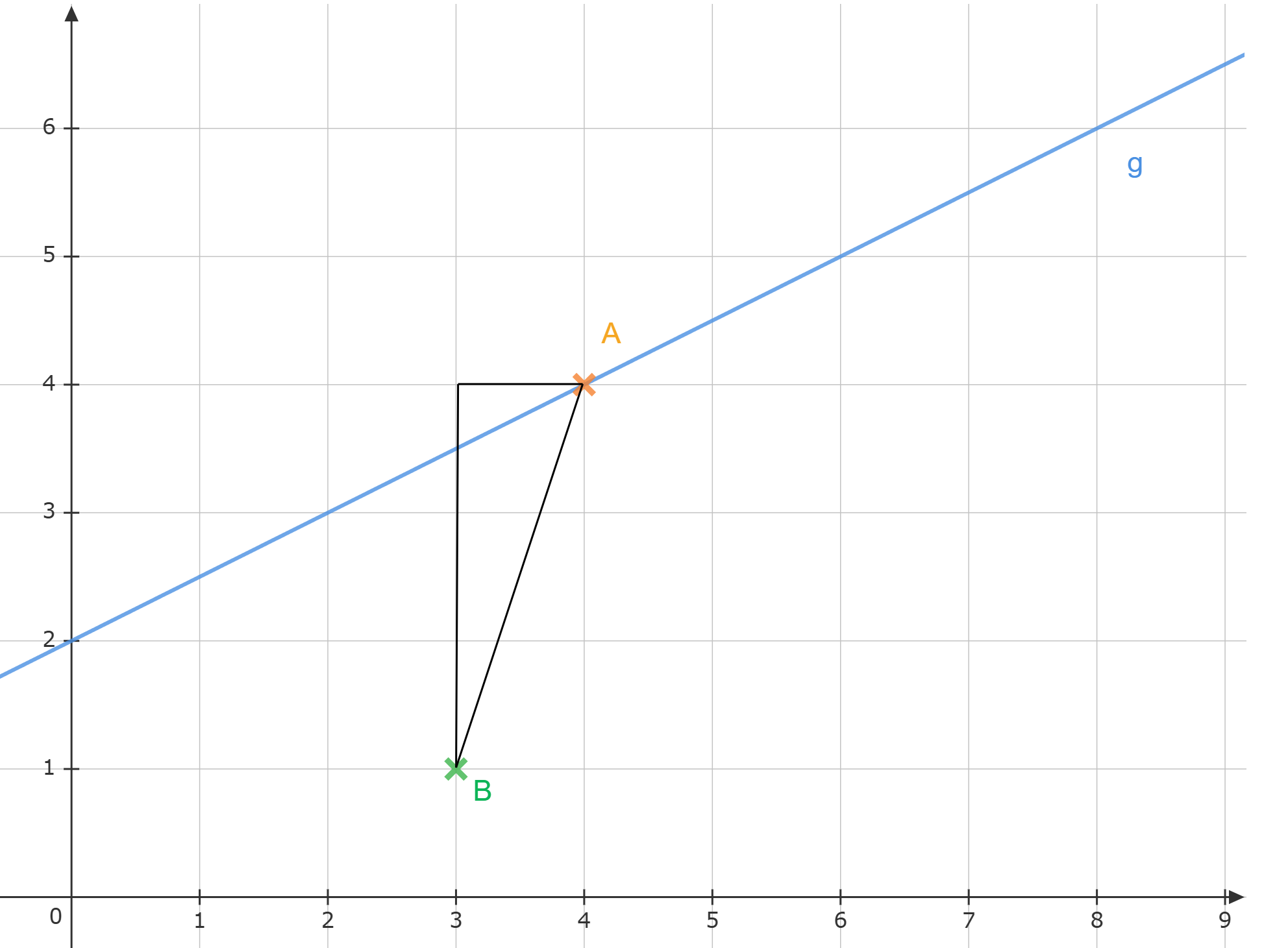
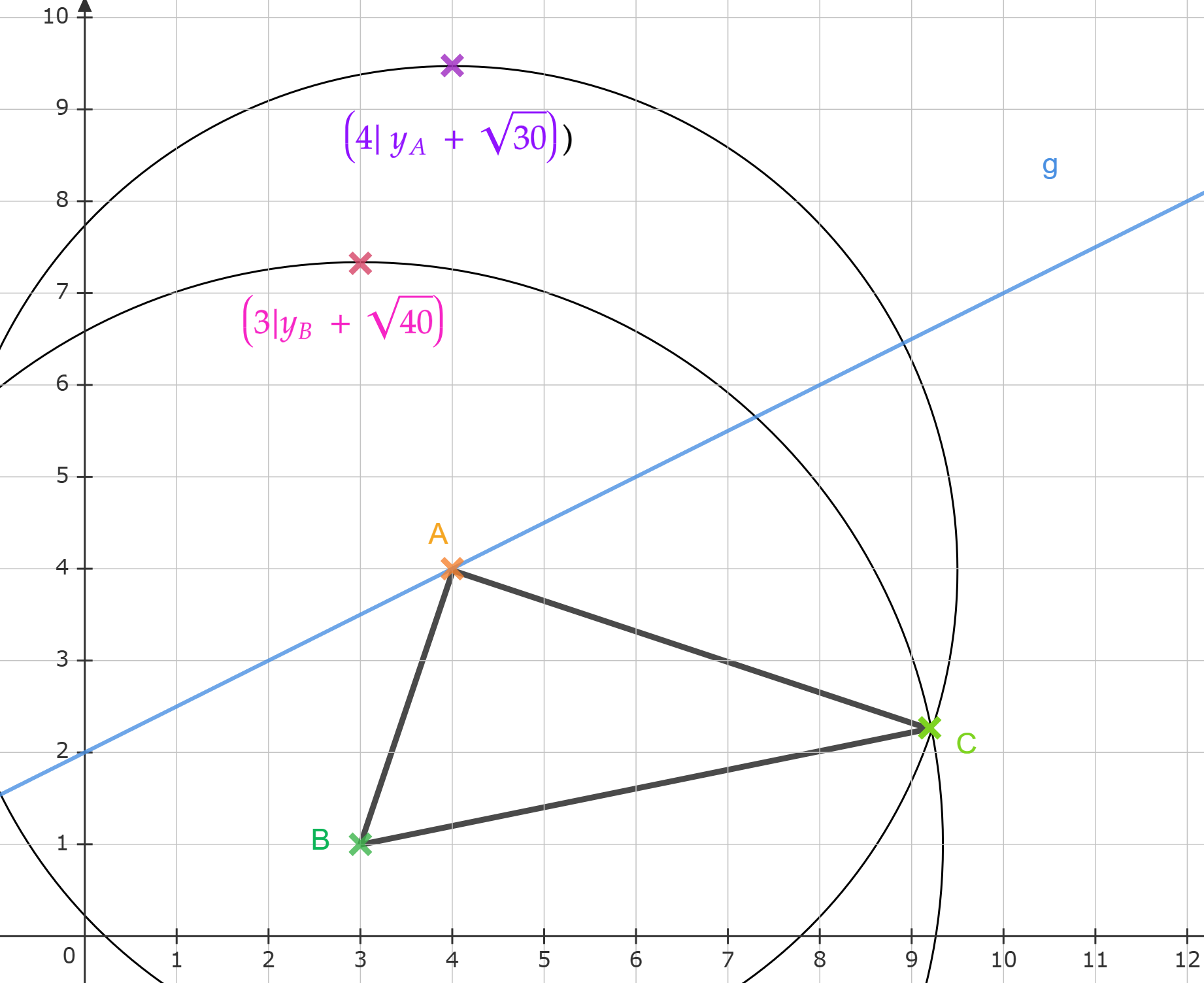
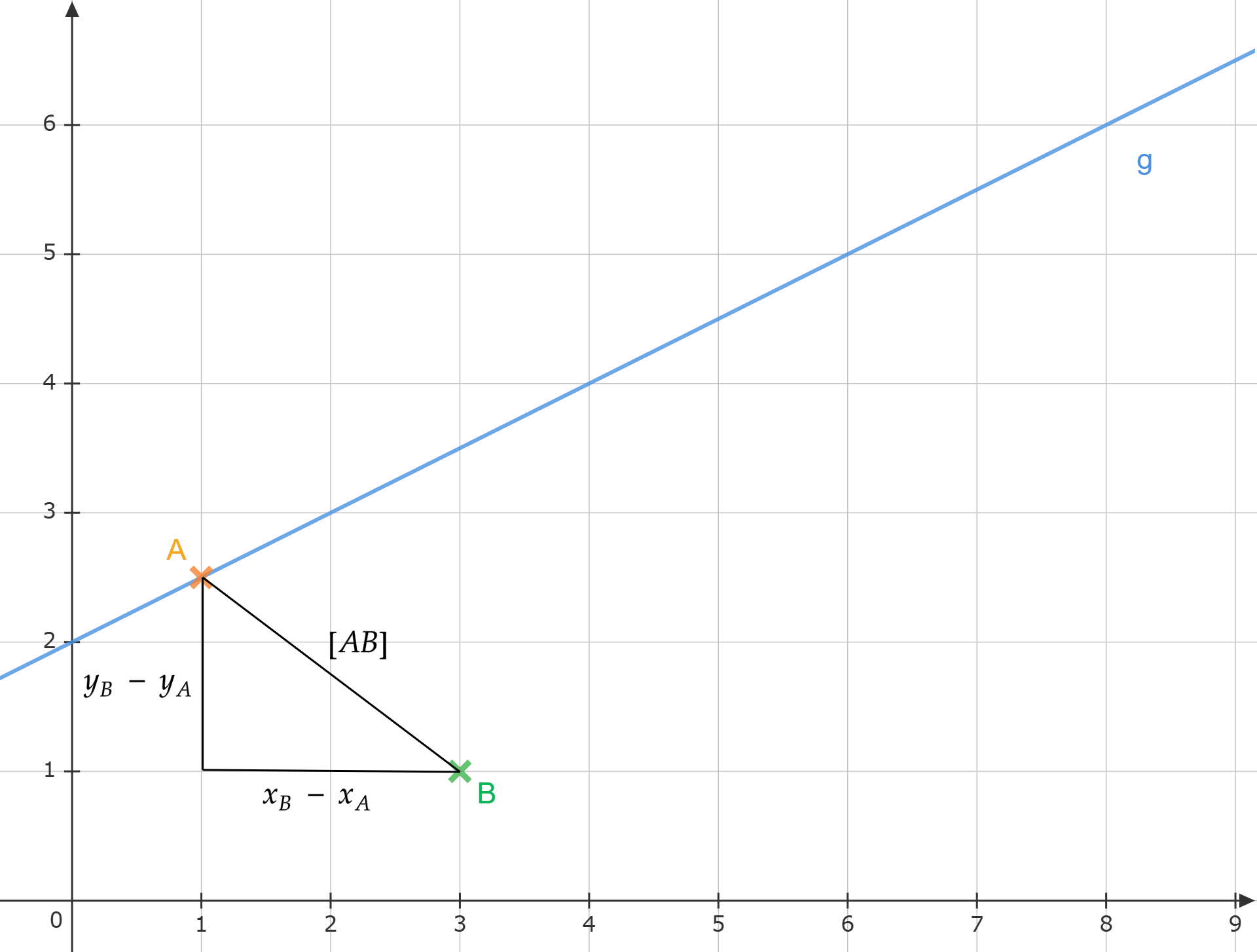
Der Punkt $\mathrm{B\ (3|1)}$ ist gemeinsamer Eckpunkt von rechtwinkligen Dreiecken $\mathrm{A_nBC_n}$ , wobei die Punkte $\mathrm{A_n(x|0{,}5x+2)}$ auf der Geraden $g$ mit der Gleichung $\mathrm{y=0{,}5x+2}$ liegen ( $\mathbb{G}=\mathbb{R}\times\mathbb{R}$ ). Die Hypotenusen $\mathrm{\left[BC_n\right]}$ sind dabei stets doppelt so lang wie die Katheten $\mathrm{[AB_n]}$ .
1. Zeichnen Sie die Dreiecke $A_1BC_1$ für $x = 1$ und $A_2BC_2$ für $x=4$ in das Koordinatensystem ein.
2. Begründen Sie, dass für die Winkel $\mathrm{C_nBA_n}$ gilt: $\mathrm{\measuredangle C_nBA_n=60°}$ .
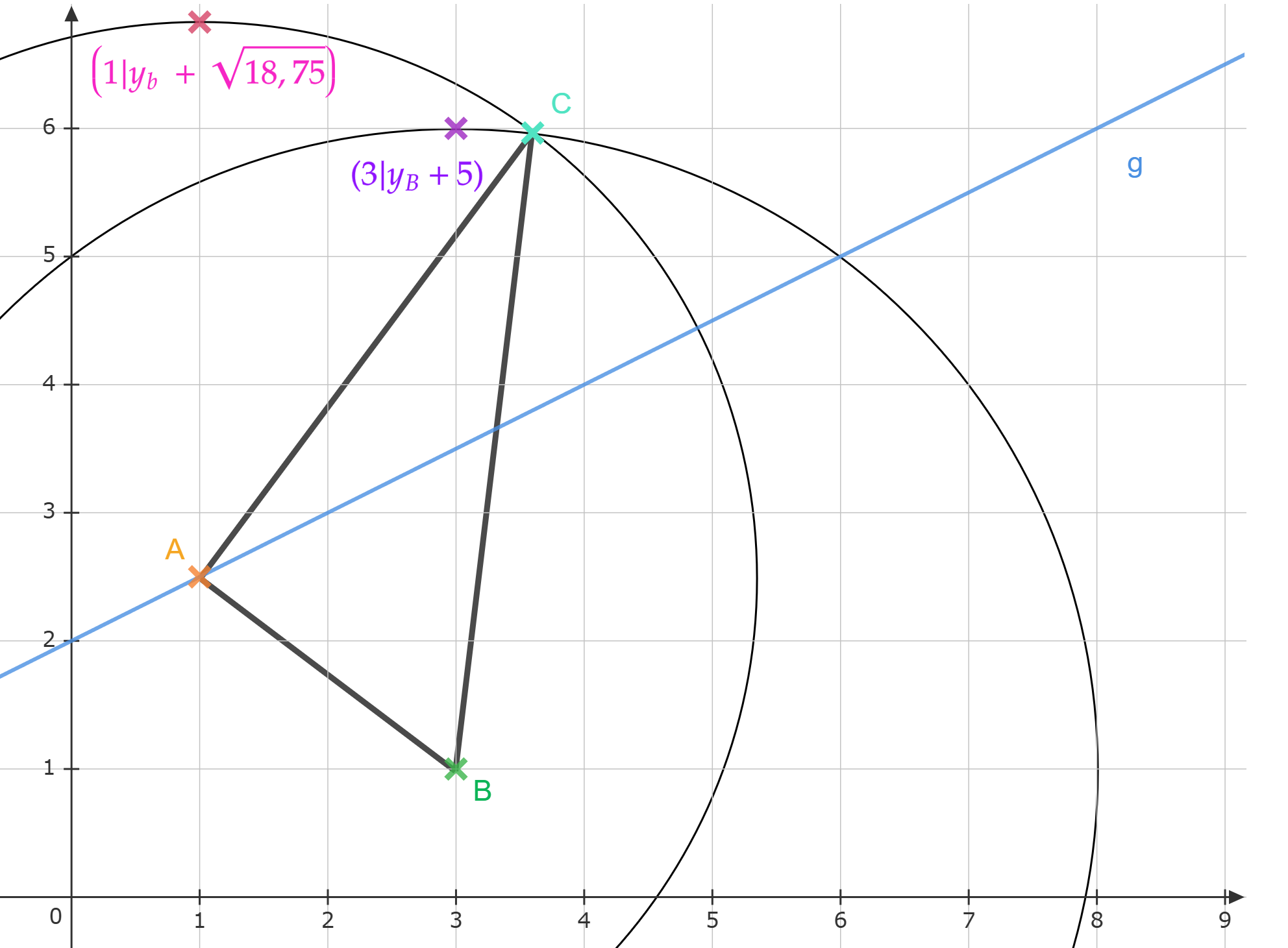
3. Zeigen Sie, dass für die Koordinaten der Punkte $\mathrm{C_n}$ in Abhängigkeit von der Abszisse $\text{x}$ der Punkte $\mathrm{A_n}$ gilt: $\ \mathrm{C_n\left(1{,}87x+1{,}73|-1{,}23x+7{,}20\right)}$ .
4. Für das Dreieck $\mathrm{A_3BC_3}$ gilt: $\mathrm{BC_3\parallel\ g}$ .
  Berechnen Sie die $\text{x}$ –Koordinate des Punktes $\text{A}$ .
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
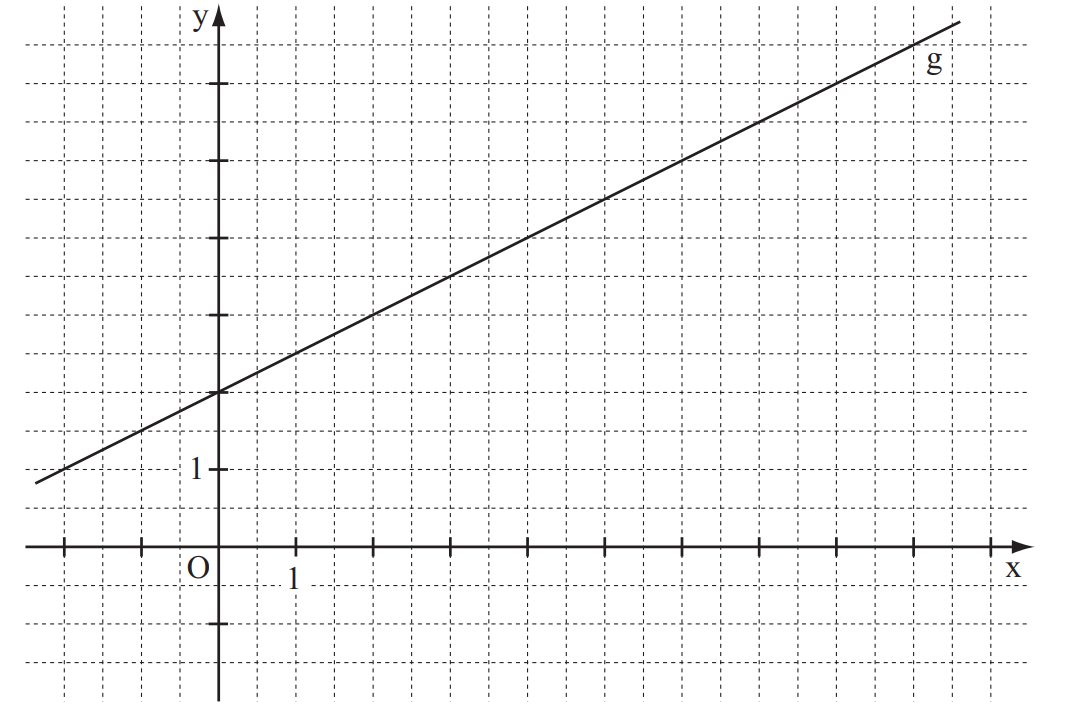
1. Die Zeichnung zeigt den Graphen der Funktion $f_1$ mit einer Gleichung der Form $y=\log_2\left(x+a\right)+b$ und die zugehörige Asymptote h $(\mathbb{G}=\mathbb{R}\times\mathbb{R};a,b\in \mathbb{R})$ .
  Der Graph zu $f_1$ schneidet die $y$ –Achse im Punkt $P (0|4)$ . Geben Sie die Werte für $a$ und $b$ an.
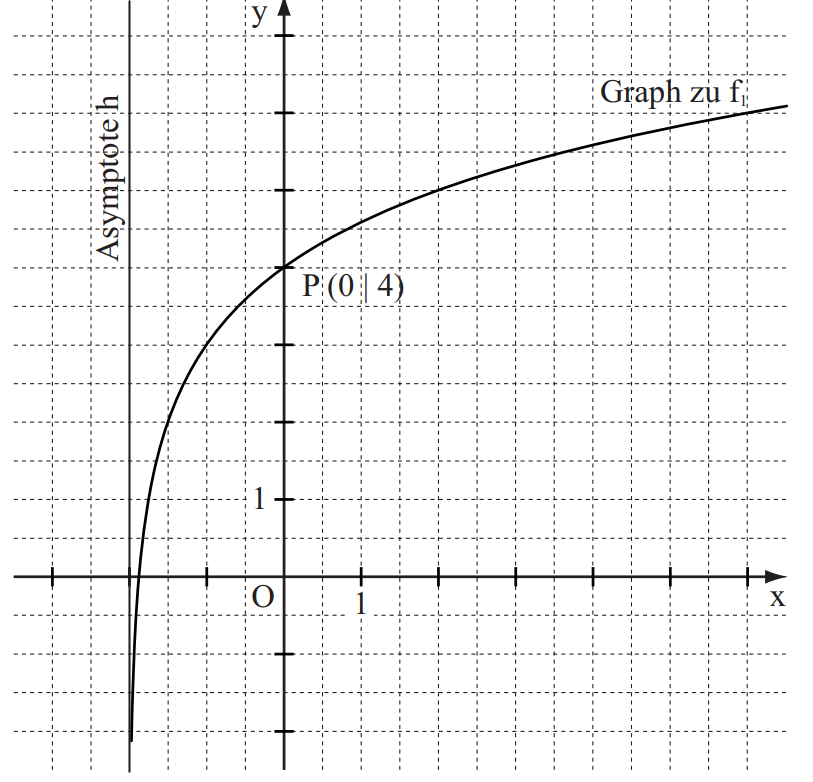
2. Die Funktion $f_2$ hat eine Gleichung der Form $y=a^{x+2}-1$ , die zugehörige Umkehrfunktion hat eine Gleichung der Form $y=\log_5(x+1)+b$ $(\mathbb{G}=\mathbb{R}\times \mathbb{R}; a,b\in \mathbb{R})$ . Bestimmen Sie die Werte für a und b sowie die Wertemenge der Funktion $f_2$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$\displaystyle \text{Mantelflächen der Kegel + Mantelflächen der Zylinder + Grundfläche der Zylinder}$
$=$	$\displaystyle r\cdot{m_\text{Kegel}\cdot{\pi}}+2\cdot{r}\cdot{\pi}\cdot{h_\text{Zylinder}}+r^2\cdot{\pi}$
	↓ Einsetzen von $m_\text{Kegel}$ und $h_\text{Zylinder}$
$=$	$\displaystyle =3\cdot{\dfrac{3}{\cos(\varphi-90)} \cdot{\pi}} +2\cdot{3}\cdot{\pi}\cdot{3\cdot{\tan(\varphi-90)}}+3^2\cdot{\pi}$
$=$	$\displaystyle =9\cdot{\pi}\cdot\{{\dfrac{1}{\cos(\varphi-90)} +2\cdot{\tan(\varphi-90)}+1\}}~\text{cm}^2$

Nachtermin Teil A

Seiten CnDn‾(φ)\overline{C_nD_n}(\varphi)Cn​Dn​​(φ)

Seiten ADn‾(φ)\overline{AD_n}(\varphi)ADn​​(φ)

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Seiten $\overline{C_nD_n}(\varphi)$

Seiten $\overline{AD_n}(\varphi)$