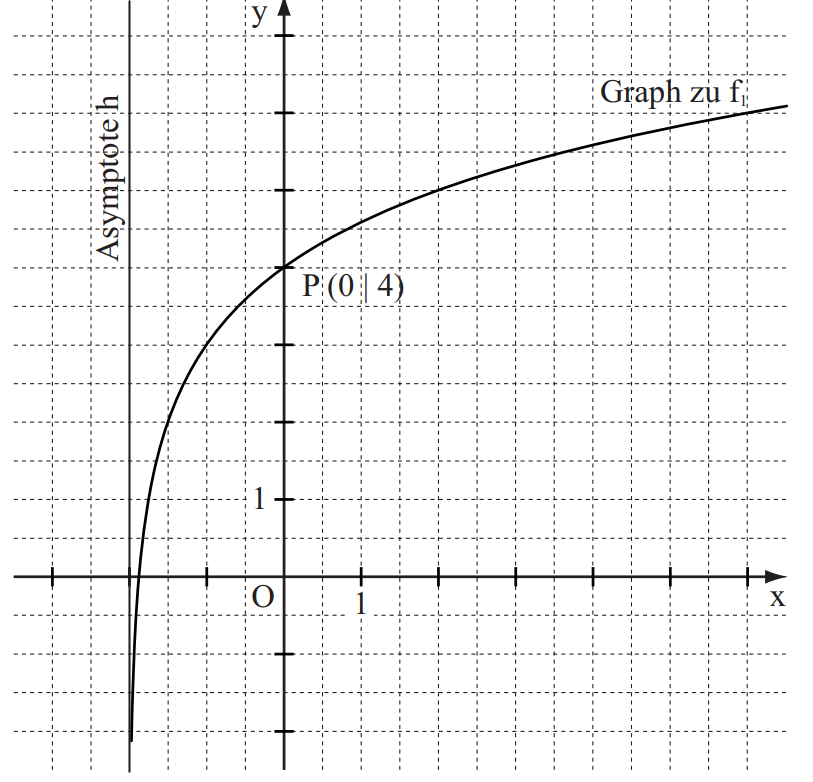
Die Zeichnung zeigt den Graphen der Funktion $f_1$ mit einer Gleichung der Form $y=\log_2\left(x+a\right)+b$ und die zugehörige Asymptote h $(\mathbb{G}=\mathbb{R}\times\mathbb{R};a,b\in \mathbb{R})$.

Der Graph zu $f_1$ schneidet die $y$–Achse im Punkt $P (0|4)$. Geben Sie die Werte für $a$ und $b$ an.

Die Funktion $f_2$ hat eine Gleichung der Form $y=a^{x+2}-1$, die zugehörige Umkehrfunktion hat eine Gleichung der Form $y=\log_5(x+1)+b$ $(\mathbb{G}=\mathbb{R}\times \mathbb{R}; a,b\in \mathbb{R})$. Bestimmen Sie die Werte für a und b sowie die Wertemenge der Funktion $f_2$.