Nachtermin Teil A - lernen mit Serlo!

Nebenstehende Skizze zeigt das Fünfeck $ABCDE$ mit dem Punkt $F\in[AE]$ . Es gilt: $\overline{DE}=4\;\text{cm};\overline{\ BF}=8\;\text{cm};\ \measuredangle AED=\measuredangle AFB=90°;\ [CF]||[DE]$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

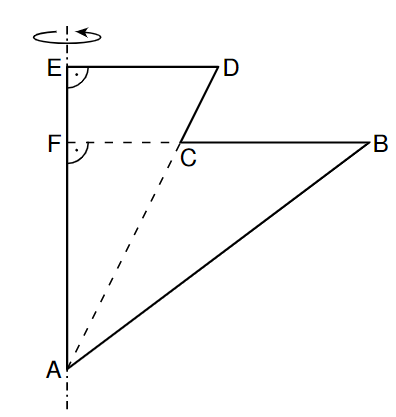
Der Kegel, der durch Rotation des Dreiecks $ADE$ um die Achse $AE$ entsteht, hat ein Volumen von $134 \;\textrm{cm}^3$ . Berechnen Sie die Höhe dieses Kegels.

$[$ Ergebnis: $\overline {AE}=8{,}00 \;\textrm{cm}$ $]$

Die Strecke $[AF]$ ist um $25\;\%$ kürzer als die Strecke $[AE]$ .

Berechnen Sie das Volumen $V$ des Rotationskörpers, der durch Rotation des Fünfecks $ABCDE$ um die Achse $AE$ entsteht.

$[$ Zwischenergebnis: $\overline {CF}=3{,}00 \,\textrm{cm}$ $]$

$\displaystyle V_{Kegel}$	$=$	$\displaystyle \frac{1}{3}\cdot\pi\cdot r^2\cdot h$
	↓	Bekannte Größen einsetzen.
$\displaystyle 134\;\text{cm}^3$	$=$	$\displaystyle \frac{1}{3}\cdot\pi\cdot(4\;\text{cm})^2\cdot h$	$\displaystyle \cdot3\| :(4\;\text{cm})^2\| :\pi$
	↓	Nach der Unbekannten auflösen.
$\displaystyle h$	$=$	$\displaystyle \dfrac{134\;\text{cm}^3\cdot3}{\pi\cdot(4\;\text{cm})^2}$
	↓	Zusammenfassen.
	$≈$	$\displaystyle 8{,}00\;\text{cm}$

$\displaystyle \dfrac{\overline {CF}}{\overline {DE}}$	$=$	$\displaystyle \dfrac{\overline {AF}}{\overline {AE}}$	$\displaystyle \cdot\overline {DE}$
$\displaystyle \overline {CF}$	$=$	$\displaystyle \dfrac{\overline {AF}\cdot \overline {DE}}{\overline {AE}}$
	$=$	$\displaystyle \dfrac{6\;\text{cm}\cdot4\;\text{cm}}{8\;\text{cm}}$
	$=$	$\displaystyle 3{,}00\;\text{cm}$

$\displaystyle V_{ABCDE}$	$=$	$\displaystyle V_{ADE}+V_{ABF}-V_{ACF}$
	$=$	$\displaystyle \left(134+\frac{1}{3}\cdot\pi\cdot8^2\cdot6-\frac{1}{3}\cdot\pi\cdot3^2\cdot6\right)\;\text{cm}^3$
	$=$	$\displaystyle (134+402{,}12-56{,}55)\;\text{cm}^3$
	$≈$	$\displaystyle 479{,}57\;\text{cm}^3$

Teilaufgabe a

Hast du eine Frage oder Feedback?

Teilaufgabe b

Hast du eine Frage oder Feedback?