Teil B - lernen mit Serlo!

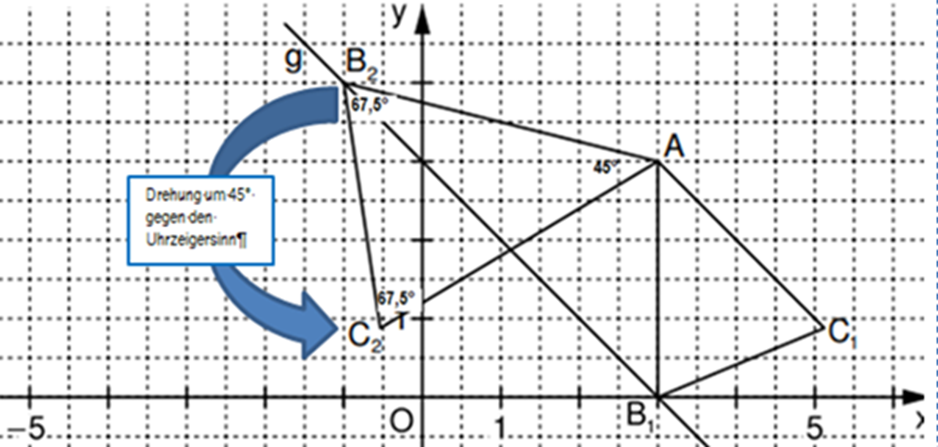
Aufgabe B1

Der Punkt $A (3 | 3)$ ist gemeinsamer Eckpunkt von gleichschenkligen Dreiecken $A B_{n} C_{n}$ mit den Basen $B_{n} C_{n}$ . Die Eckpunkte $B_{n} (x | - x + 3)$ der Dreiecke $A B_{n} C_{n}$ liegen auf der Geraden $g$ mit der Gleichung $y = - x + 3$ $(x, y \in ℝ)$ .

Es gilt: $∢ B_{n} A C_{n} = 45^{\circ}$ .

In das Koordinatensystem sind die Gerade $g$ und das Dreieck $A B_{1} C_{1}$ für $x = 3$ bereits eingezeichnet.
Ergänzen Sie das Dreieck $A B_{2} C_{2}$ für $x = - 1$ . (1 P)
Bestimmung von $B_{2}$ mithilfe von $B_{n}$
Hierfür setzen wir $x = - 1$ in die allgemeine Form von $B_{n}$ ein und erhalten so $B_{2}$
$B_{2} (- 1 | - (- 1) + 3)$ $\Rightarrow$ $B_{2} (- 1 | 4)$
Wir zeichnen nun $B_{2}$ in unser Koordinatensystem ein.
Berechnung der fehlenden Winkel
Der Winkel $∢ B_{n} A C_{n}$ beträgt $45 °$
Wir wissen, dass die Innenwinkelsumme eines Dreiecks $180 °$ beträgt.
Da es sich um ein Gleichschenkliges Dreieck handelt, gilt: $∢ C_{n} B_{n} A = ∢ A C_{n} B_{n}$
Wir rechnen: $∢ C_{n} B_{n} A = ∢ A C_{n} B_{n} = \frac{180 - 45}{2} = 67,5 °$
Vervollständigung der Zeichnung
Schenkel mit $∢ A B_{2} C_{2} = 67,5 °$ in $B_{2}$ an $A B_{2}$ antragen
Schenkel mit $∢ C_{2} A B_{2} = 45 °$ in $A$ an $A B_{2}$ antragen
Schenkel schneiden sich in Punkt $C_{2}$
Verbinde die Strecken $B_{2} C_{2}$ und $A C_{2}$
Gerade $g$ mit Dreiecke $A B_{1} C_{1}$ und $A B_{2} C_{2}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme zunächst $B_{2}$ mithilfe von $B_{n}$ , indem du $x = - 1$ einsetzt.
Berechne die Innenwinkel des Dreiecks.
Bestimme $C_{2}$ zeichnerisch mithilfe der berechneten Winkelwerte.

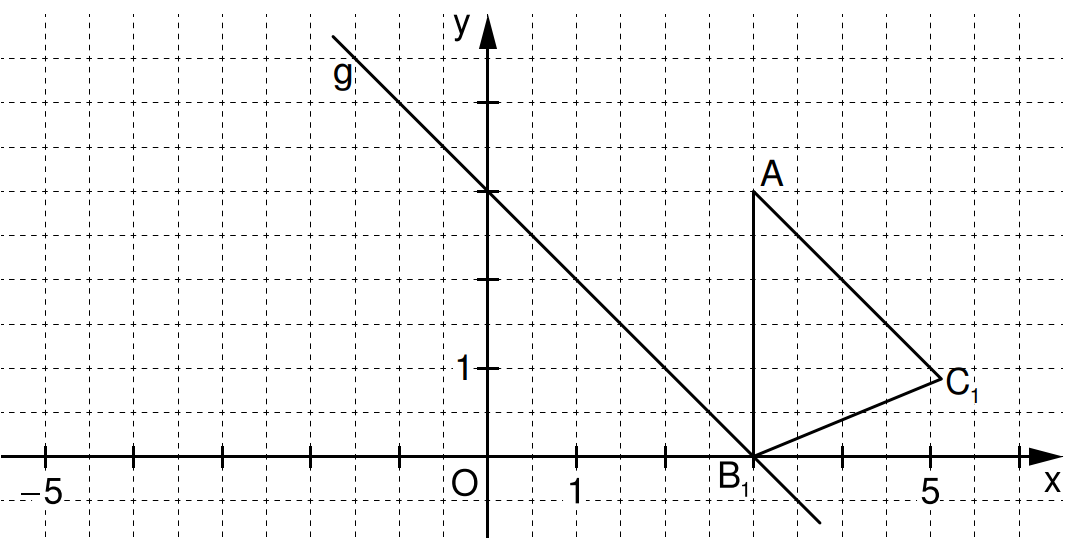
Berechnen Sie die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ . (4 P)

Runden Sie auf zwei Stellen nach dem Komma.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$\vec{A C_{n}} (x)$	$=$	$\underset{Beschreibt die Drehung von \vec{A B_{n}}}{\underset{⏟}{R_{α} ⊙ \vec{A B_{n}}}}$
	↓	Die Matrix und den Vektor einsetzen.
	$=$	$(\begin{array}{cc} \cos α & - \sin α \\ \sin α & \cos α \end{array}) ⊙ (\begin{array}{c} x - 3 \\ - x + 3 - 3 \end{array})$
	$=$	$(\begin{array}{cc} \cos (45) & - \sin (45) \\ \sin (45) & \cos (45) \end{array}) ⊙ (\begin{array}{c} x - 3 \\ - x + 3 - 3 \end{array})$
	$=$	$(\begin{array}{cc} 0,71 & - 0,71 \\ 0,71 & 0,71 \end{array}) ⊙ (\begin{array}{c} x - 3 \\ - x \end{array})$
	↓	$Multiplikationsregel: (\begin{array}{c} x^{^{'}} \\ y^{^{'}} \end{array}) = (\begin{array}{cc} a & b \\ c & d \end{array}) ⊙ (\begin{array}{c} x \\ y \end{array}) = (\begin{array}{c} a \cdot x + b \cdot y \\ c \cdot x + d \cdot y \end{array})$
	$=$	$(\begin{array}{c} 0,71 \cdot (x - 3) + (- 0,71) \cdot (- x) \\ 0,71 \cdot (x - 3) + 0,71 \cdot (- x) \end{array})$
	$=$	$(\begin{array}{c} 0,71 x - 3 \cdot 0,71 + (- 0,71) \cdot (- x) \\ 0,71 x - 3 \cdot 0,17 - 0,71 x \end{array}) = (\begin{array}{c} 1,42 x - 2,13 \\ - 2,13 \end{array})$

Aufgabe B1

Bestimmung von $B_{2}$ mithilfe von $B_{n}$

Berechnung der fehlenden Winkel

Vervollständigung der Zeichnung

Hast du eine Frage oder Feedback?

Wir überlegen uns, woraus sich $C_{n}$ zusammensetzt:

Gleichung für $\vec{A C_{n}}$ mit Drehmatrix und Vektor $\vec{A B_{n}}$ aufstellen:

Berechnung $\vec{O C_{n}}$

Hast du eine Frage oder Feedback?

Aufgabe B1

Bestimmung von B2 mithilfe von Bn

Berechnung der fehlenden Winkel

Vervollständigung der Zeichnung

Hast du eine Frage oder Feedback?

Wir überlegen uns, woraus sich Cn zusammensetzt:

Gleichung für ACn→ mit Drehmatrix und Vektor ABn→ aufstellen:

Berechnung OCn→

Hast du eine Frage oder Feedback?

Bestimmung von $B_{2}$ mithilfe von $B_{n}$

Wir überlegen uns, woraus sich $C_{n}$ zusammensetzt:

Gleichung für $\vec{A C_{n}}$ mit Drehmatrix und Vektor $\vec{A B_{n}}$ aufstellen:

Berechnung $\vec{O C_{n}}$