Teil A - lernen mit Serlo!

Das gleichschenklige Dreieck $ABC$ mit der Basis $[BC]$ und der Höhe $[AM]$ ist die Grundfläche der Pyramide $ABCS$ mit der Spitze $S$ . Der Punkt $D \in [AM]$ ist der Fußpunkt der Pyramidenhöhe $[DS]$ , die senkrecht auf der Grundfläche steht.

Es gilt: $\overline{AM}=8 \ \text{cm};\overline{BC}=10\ \text{cm};\;\overline{AD}=4{,}5\ \text{cm};\overline{DS}=8{,}5\ \text{cm}.$

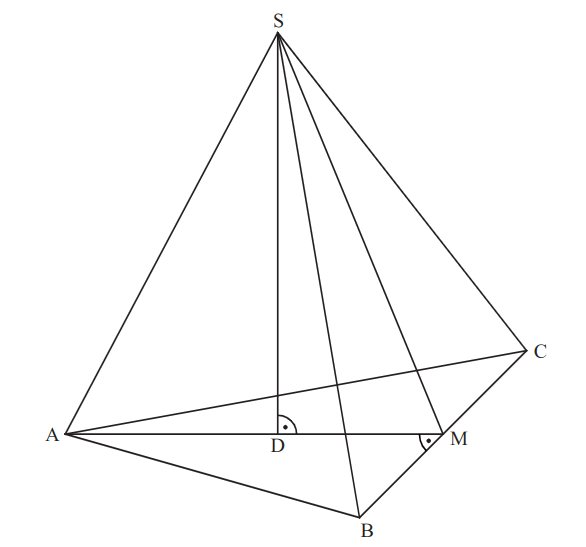
Die untenstehende Zeichnung zeigt ein Schrägbild der Pyramide $ABCS$ .

In der Zeichnung gilt: $q=\frac12;\;\;\omega=45^\circ$ . $[AM]$ liegt auf der Schrägbildachse.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Berechnen Sie das Maß des Winkels $\angle MAC$ .
[Ergebnis: $\angle MAC=32{,}01^\circ$ ]

Maß des Winkels $\measuredangle MAC$ im rechtwinkligen Dreiecks AMC (grün) mithilfe der Trigonometrie:
$\tan\left(\measuredangle MAC\right)=\frac{Gegenkathete}{Ankathete}=\frac{\overline{MC}}{\overline{AM}}$
$\tan\left(\measuredangle MAC\right)=\dfrac{5\;\text{cm}}{8\;\text{cm}}$
$\tan\left(\measuredangle MAC\right)=0{,}625$ | $\tan^{-1}$
$\measuredangle MAC\approx32{,}01^\circ$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Punkte $P_n$ liegen auf der Strecke $[DS]$ . Die Winkel $\angle DAP_n$ haben das Maß $\varphi$ mit $\varphi\in\rbrack\;0^\circ;\;62{,}10^\circ\lbrack$ .
Zeichnen Sie den Punkt $P_1$ und die Strecke $[AP_1]$ für $\varphi=40°$ in das Schrägbild zur Pyramide in der Aufgabenstellung ein.

Zeichnung des Punktes $P_1$ mit
$\measuredangle MAP_1=\varphi=40^\circ$ :
Trage einen $40^\circ$ -Winkel an Punkt A ab (siehe Abbildung rot).
Der Schnittpunkt mit der Höhe [DS] ist der Punkt $P_1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Durch die Punkte $P_n$ verlaufen zur Grundfläche $ABC$ parallele Ebenen, die die Kanten der Pyramide $ABCS$ in Punkten $E_n\in\lbrack AS\rbrack$ , $F_n\in\lbrack BS\rbrack$ und $G_n\in\lbrack CS\rbrack$ und die Strecke $[MS]$ in Punkten $N_n$ schneiden. Die Dreiecke $E_nF_nG_n$ sind die Grundflächen von Pyramiden $E_nF_nG_nD$ mit der Spitze $D$ .
Zeichnen Sie die Pyramide $E_1F_1G_1D$ und den Punkt $N_1$ in das Schrägbild zur Pyramide in der Aufgabenstellung ein.
Zeichnung der Pyramide $E_1F_1G_1D$ :
Zeichne eine Parallele durch den Punkt $P_1$ zu [AM] (rot).
Die Parallele schneidet [AS] in Punkt $E_1$ und [MS] in Punkt $N_1$ .
Konstruiere dann einen $45^\circ$ -Winkel in $N_1$ (blau)
(Alternativ: eine Parallele durch $N_1$ zu [BC].)
Die Parallele schneidet [CS] in $G_1$ und [BS] in $F_1$ (nächste Abbildung).
Verbinde nun alle Eckpunkte miteinander (inklusive der Spitze D).
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Berechnen Sie die Längen der Strecken $[DP_n]$ und $[E_nN_n]$ in Abhängigkeit von $\varphi$ .

[Ergebnisse: $\overline{DP_n}(\varphi)=4{,}5\cdot\tan\left(\varphi\right)\ \text{cm};\;\overline{E_nN_n}(\varphi)=(8-4{,}24\cdot\tan\left(\varphi\right))\ \text{cm}$ ].

Länge der Strecke [ $DP_n$ ] in Abhängigkeit von $\varphi$ im rechtwinkligen Dreieck $ADP_1$ mithilfe der Trigonometrie:

$\tan\left(\measuredangle DAP_1\right)=\frac{Gegenkathete}{Ankathete}=\frac{\overline{DP_1}}{\overline{AD}}$

$\tan\ \varphi=\dfrac{\overline{DP_1}}{4{,}5\;\text{cm}}$ | $\cdot 4{,}5\;\text{cm}$

$\overline{DP_1}\left(\varphi\right)=\tan\varphi\cdot4{,}5\;\text{cm}$

$\overline{DP_1}\left(\varphi\right)=4{,}5\cdot\tan\varphi\;\text{cm}$

Länge der Strecke [ $E_nN_n$ ] in Abhängigkeit von $\varphi$ mithilfe des Strahlensatzes (Vierstreckensatz):

$\dfrac{\overline{DS}}{\overline{P_{1}S}}=\dfrac{\overline{AM}}{\overline{E_nN_n}}$

(mit $\overline{P_1S}=\overline{DS}-\overline{DP_n}$ )

$\displaystyle \frac{8{,}5}{8{,}5-4{,}5\cdot\tan\varphi}$	$=$	$\displaystyle \frac{8}{\overline{E_nN_n}}$
	↓	Löse nach $\overline{E_nN_n}$ auf.
$\displaystyle \frac{8{,}5}{8{,}5-4{,}5\cdot\tan\varphi}$	$=$	$\displaystyle \frac{8}{\overline{E_nN_n}}$	$\displaystyle \cdot\overline{E_nP_n}$
$\displaystyle \frac{8{,}5\cdot\overline{E_nN_n}}{8{,}5-4{,}5\cdot\tan\varphi}$	$=$	$\displaystyle 8$	$\displaystyle \cdot(8{,}5-4{,}5\cdot\tan\varphi)$
$\displaystyle 8{,}5\cdot\overline{E_nP_n}$	$=$	$\displaystyle 8\cdot\left(8{,}5-4{,}5\cdot\tan\varphi\right)$	$\displaystyle :8{,}5$
$\displaystyle \overline{E_nN_n}\left(\varphi\right)$	$=$	$\displaystyle \frac{8\cdot8{,}5-8\cdot4{,}5\cdot\tan\varphi}{8{,}5}$
	$=$	$\displaystyle 8-\frac{72}{17}\cdot\tan\varphi$
	$=$	$\displaystyle 8-4{,}24\cdot\tan\varphi$

Ergebnis:

$\overline{E_nN_n}\left(\varphi\right)\approx\left(8-4{,}24\cdot\tan\varphi\ \right)\;\text{cm}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Berechnen Sie das Volumen der Pyramide $E_1F_1G_1D$ .
Volumen der Pyramide $E_1F_1G_1D$ mit:
allgemeine Formel: $V=\frac{1}{3}\cdot G\cdot h$
Die Höhe $h$ berechnen wir wie folgt:
$h=\overline{DP_1}\left(40^\circ\right)=4{,}5\cdot\tan\left(40^\circ\right)cm\approx3{,}78\;\text{cm}$
Die Grundfläche berechnen wir mit folgender Formel: $G=\frac{1}{2}\cdot\overline{E_1N_1}\cdot\overline{F_1G_1}$
$\overline{E_1N_1}=\left(8-4{,}24\cdot\tan\varphi\ \right)\;\text{cm}=\left(8-4{,}24\cdot\tan\left(40^\circ\right)\right)\;\text{cm}\approx4{,}44\;\text{cm}$
$\overline{F_1G_1}=2\cdot\overline{N_1G_1}\$ (rot)
$\overline{N_1G_1}\$ können wir mit Hilfe der Trigonometrie im rechtwinkligen Dreieck $E_nN_nG_n$ berechnen:
Wichtig: Wir benötigen einen Winkel, da die Dreiecke $ABC$ und $E_1F_1G_1$ (ebenso: $\triangle AMC$ und $\triangle E_1N_1G_{1}$ ) ähnlich sind, sind ihre Winkel ebenso gleich groß (neongrün):
$\measuredangle MAC=\measuredangle N_1E_1G_1=32{,}01^\circ$
$\tan\left(\measuredangle N_1E_1G_1\right)=\dfrac{\text{Gegenkathete}}{\text{Ankathete}}=\dfrac{\overline{N_1G_1}}{\overline{E_1N_1}}$
$\tan\left(32{,}01^\circ\right)=\dfrac{\overline{N_1G_1}}{4{,}44\ cm}$ | $\cdot4{,}44\;\text{cm}$
$\overline{N_nG_n}=\tan\left(32{,}01°\right)\cdot4{,}44\ cm\approx2{,}78\;\text{cm}$
Damit ist die Seite $\overline{F_1G_1}=2\cdot\overline{N_1G_1}=2\cdot2{,}78\;\text{cm}\approx5{,}55\;\text{cm}$
Einsetzen in die Volumenformel:
$V=\frac{1}{3}\cdot G\cdot h=\frac{1}{3}\cdot\frac{1}{2}\cdot\overline{E_1N_1}\cdot\overline{F_1G_1}\cdot\overline{DP_1}=\left(\frac{1}{3}\cdot\frac{1}{2}\cdot4{,}44\cdot5{,}55\cdot3{,}78\right)\;\text{cm}^3\approx15{,}52\;\text{cm}^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇