Nachtermin Teil B - lernen mit Serlo!

Gegeben sind die Geraden $g$ mit der Gleichung $y = 0,25 x + 6$ und $h$ mit der Gleichung $y = x - 1$ $(𝔾 = ℝ \times ℝ)$ . Punkte $D_{n} (x | x - 1)$ mit der Abszisse $x$ liegen auf der Geraden $h$ . Punkte $A_{n}$ auf der Geraden $g$ haben eine um $2$ kleinere Abszisse als die Punkte $D_{n}$ .

Die Punkte $A_{n}$ und $D_{n}$ bilden zusammen mit Punkten $B_{n}$ und $C_{n}$ Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ mit den Symmetrieachsen $A_{n} C_{n}$ .

Es gilt: $∢ B_{n} A_{n} D_{n} = 90^{\circ}; A_{n} C_{n} = 1,5 \cdot B_{n} D_{n}$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

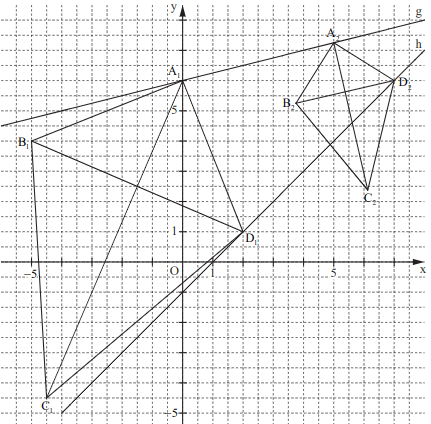
Zeichnen Sie die Geraden $g$ und $h$ sowie die Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ für $x = 2$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 7$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1$ cm; $- 6 \leq x \leq 8; - 5 \leq y \leq 8$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
Zeichne zunächst ein Koordinatensystem mit $- 6 \leq x \leq 8$ und $- 5 \leq x \leq 8$ .
Bestimme für die beiden Geraden $g$ und $h$ jeweils $2$ Punkte, die auf diesen Geraden liegen, z.B. $P_{1} (0 | 6)$ und $P_{2} (1 | 6,25)$ für die Gerade $g$ , sowie $Q_{1} (0 | - 1)$ und $Q_{2} (1 | 0)$ für die Gerade $h$ .
Die Gerade $g$ erhältst Du, indem Du eine Gerade durch die beiden Punkte $P_{1} (0 | 6)$ und $P_{2} (1 | 6,25)$ zeichnest.
Die Gerade $h$ erhältst Du, indem Du eine Gerade durch die beiden Punkte
$Q_{1} (0 | - 1)$ und $Q_{2} (1 | 0)$ zeichnest.
Berechne nun die Koordinaten der Punkte $A_{1}, B_{1}, C_{1}, D_{1}$ .
Für $x = 2 \Rightarrow D_{1} (2 | 1)$ . $A_{1}$ liegt auf $g$ und hat eine um $2$ kleinere Abszisse wie $D_{1}$ $\Rightarrow A_{1} (0 | 6) .$
Verbinde $A_{1}$ und $D_{1}$ und trage in $A_{1}$ einen $90 °$ Winkel an. Du erhältst den Punkt $B_{1}$ indem Du auf dem freien Schenkel des Winkels die Länge $A_{1} D_{1}$ anträgst.
Verbinde nun $A_{1}$ mit dem Mittelpunkt der Strecke $B_{1} D_{1}$ durch eine Gerade. Markiere auf dieser Geraden den Punkt, der von $A_{1}$ den Abstand $1,5 \cdot B_{1} D_{1}$ hat. Dieser Punkt ist der gesuchte Punkt $C_{1}$ .
Verbinde die Punkte $A_{1}, B_{1}, C_{1}, D_{1}$ zu dem 1. Drachenviereck. Ermittle die Punkte $A_{2}, B_{2}, C_{2}, D_{2}$ für das 2. Drachenviereck analog.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnen Sie die Koordinaten der Punkte $A_{n}$ und $B_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $D_{n}$ .
[Ergebnisse: $A_{n}$ $(x - 2 | 0,25 x + 5,5)$ ; $B_{n}$ $(1,75 x - 8,5 | 0,25 x + 3,5)$ ]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
Die $x$ -Koordinate der Punkte $A_{n}$ ergibt sich, indem Du $x$ durch $(x - 2)$ ersetzt. Die zugehörige $y$ -Koordinate ermittelst Du, indem Du $(x - 2)$ an Stelle von $x$ in die Gleichung für $g$ einsetzt.
$A_{n} (x - 2 | 0,25 (x - 2) + 6)$ $= A_{n} (x - 2 | 0,25 x + 5,5)$
Den Punkt $B_{n}$ erhältst Du, indem Du an den Punkt $A_{n}$ den Vektor $\vec{A_{n} B_{n}}$ anlegst.
$\vec{O B_{n}} = \vec{O A_{n}} + \vec{A_{n} B_{n}}$
$\vec{A_{n} D_{n}} (x) = (\begin{array}{c} x - (x - 2) \\ x - 1 - (0,25 x + 5,5) \end{array})$ $x \in ℝ$
$\vec{A_{n} D_{n}} (x) =$ $(\begin{array}{cc} 2 \\ 0,75 x - 6,5 \end{array})$
$\vec{A_{n} D_{n}}$ $\to \vec{A_{n} B_{n}}$ $(O; φ = 90 °)$
$\vec{A_{n} B_{n}} (x) = (\begin{array}{cc} 0,75 x - 6,5 \\ - 2 \end{array})$
$\vec{O B_{n}} (x) = (\begin{array}{c} x - 2 \\ 0,25 x + 5,5 \end{array})$ $+$ $(\begin{array}{cc} 0,75 x - 6,5 \\ - 2 \end{array})$ $x \in ℝ$
$\vec{O B_{n}} (x) = (\begin{array}{c} 1,75 x - 8,5 \\ 0,25 x + 3,5 \end{array})$
$B_{n} (1,75 x - 8,5 | 0,25 x + 3,5)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Diagonale [ $B_{3} D_{3}$ ] des Drachenvierecks $A_{3} B_{3} C_{3} D_{3}$ liegt parallel zur Geraden $g$ . Berechnen Sie die Abszisse $x$ des Punktes $D_{3}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
$\vec{B_{n} D_{n}} (x) = (\begin{array}{cc} x - (1,75 x - 8,5)) \\ x - 1 - (0,25 x + 3,5)) \end{array})$ $= (\begin{array}{cc} - 0,75 x + 8,5 \\ 0,75 x - 4,5 \end{array})$
Da die Diagonale des Drachenvierecks $A_{3} B_{3} C_{3} D_{3}$ parallel zur Geraden $g$ ist,
haben die Diagonale und die Gerade $g$ dieselbe Steigung.
$m_{B_{3} D_{3}} = m_{g}$

$\frac{0,75 x - 4,5}{- 0,75 x + 8,5} = 0,25$
$0,75 x - 4,5 = 0,25 \dot{(} - 0,75 x + 8,5)$
$3 x - 18 = - 0,75 x + 8,5$
$3,75 x = 26,5$
$x = 7,07$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeigen Sie, dass für den Flächeninhalt $A$ der Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ in Abhängigkeit von $x$ gilt:
$A (x) =$ $(0,84 x^{2} - 14,63 x + 69,38) FE$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
Für diese Teilaufgabe benötigst Du die Formel, wie man den Flächeninhalt eines Drachenvierecks berechnet.
$A_{A_{n} B_{n} C_{n} D_{n}} = 0,5 \cdot A_{n} C_{n} \cdot B_{n} D_{n}$
Laut Angabe gilt: $A_{n} C_{n} = 1,5 \cdot B_{n} D_{n}$
$\Rightarrow A_{A_{n} B_{n} C_{n} D_{n}} = 0,5 \cdot 1,5 \cdot (B_{n} D_{n})^{2}$
Für die Berechnung von $B_{n} D_{n} (x)$ benutze den Satz des Pythagoras.
$B_{n} D_{n} (x) = \sqrt{(- 0,75 x + 8,5)^{2} + (0,75 x - 4,5)^{2}} LE$
$A_{A_{n} B_{n} C_{n} D_{n}} (x) = 0,5 \cdot 1,5 (\sqrt{(- 0,75 x + 8,5)^{2} + (0,75 x - 4,5)^{2}})^{2} FE$
$A_{A_{n} B_{n} C_{n} D_{n}} (x) = 0,5 \cdot 1,5 \cdot [(- 0,75 x + 8,5)^{2} + (0,75 x - 4,5)^{2}] FE$
$A_{A_{n} B_{n} C_{n} D_{n}} (x) = 0,75 \cdot [(0,5625 x^{2} - 12,75 x + 72,25) + (0,5625 x^{2} - 6,75 x + 20,25)] FE$
$A_{A_{n} B_{n} C_{n} D_{n}} (x) = 0,75 \cdot (1,125 x^{2} - 19,5 x + 92,5) FE$
$A_{A_{n} B_{n} C_{n} D_{n}} (x) = (0,84 x^{2} - 14,63 x + 69,38) FE$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Im Drachenviereck $A_{4} B_{4} C_{4} D_{4}$ haben die Punkte $A_{4}$ und $C_{4}$ dieselbe Abszisse. Berechnen Sie den Flächeninhalt des Drachenvierecks $A_{4} B_{4} C_{4} D_{4}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
Im Drachenviereck $A_{4} B_{4} C_{4} D_{4}$ gilt: $y_{B_{4}} = y_{D_{4}}$ .
$0,25 x + 3,5 = x - 1$
$4,5 = 0,75 x$
$x = 6$
$A_{A_{4} B_{4} C_{4} D_{4}} (6) = 0,84 \cdot (6)^{2} - 14,63 \cdot 6 + 69,38$
$A_{A_{4} B_{4} C_{4} D_{4}} = 30,24 - 87,78 + 69,38 = 11,84 FE$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?