Nachtermin Teil B

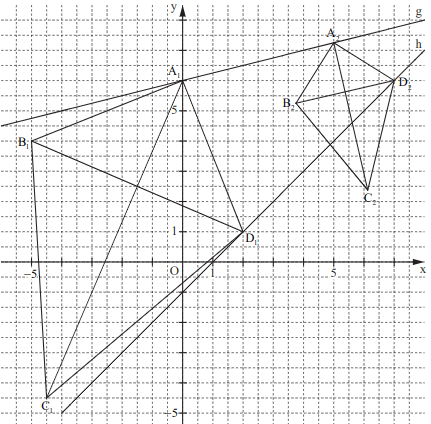
1.0 Gegeben sind die Geraden $\sf g$ mit der Gleichung $\sf y=0{,}25x+6$ und $\sf h$ mit der Gleichung $\sf y=x-1$ ( $\sf \mathbb{G}$$\sf =$$\sf \mathbb{R}$ $\sf \times$ $\sf \mathbb{R}$ ). Punkte $\sf D_n(x\vert x-1)$ mit der Abszisse $\sf x$ liegen auf der Geraden $\sf h$. Punkte $\sf A_n$ auf der Geraden $\sf g$ haben eine um $\sf 2$ kleinere Abszisse als die Punkte $\sf D_n$. Die Punkte $\sf A_n$ und $\sf D_n$ bilden zusammen mit Punkten $\sf B_n$ und $\sf C_n$ Drachenvierecke $\sf A_nB_nC_nD_n$ mit den Symmetrieachsen $\sf A_nC_n$.

Es gilt: $\sf \angle B_nA_nD_n=90^\circ;\;\overline{A_nC_n}=1{,}5\cdot\overline{B_nD_n}$.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

1.1 Zeichnen Sie die Geraden $\sf g$ und $\sf h$ sowie die Drachenvierecke $\sf A_1B_1C_1D_1$ für$\sf x=2$ und $\sf A_2B_2C_2D_2$ für $\sf x=7$ in ein Koordinatensytem.

Für die Zeichnung: Längeneinheit $\sf 1$ cm;

$\sf -6\leq x\leq8;\;\;-5\leq y\leq8$.

1.2 Berechnen Sie die Koordinaten der Punkte $\sf A_n$ und $\sf B_n$ in Abhängigkeit von der Abszisse $\sf x$ der Punkte $\sf D_n$.

[Ergebnisse: $\sf A_n$$\sf (x-2|0{,}25x+5{,}5)$; $\sf B_n$$\sf (1{,}75x-8{,}5|0{,}25x+3{,}5)$]

1.3 Die Diagonale [$\sf B_3D_3$] des Drachenvierecks $\sf A_3B_3C_3D_3$ liegt parallel zur Geraden $\sf g$. Berechnen Sie die Abszisse $\sf x$ des Punktes $\sf D_3$.

1.4 Zeigen Sie, dass für den Flächeninhalt $\sf A$ der Drachenvierecke $\sf A_nB_nC_nD_n$ in Abhängigkeit von $\sf x$ gilt:

$\sf A(x) =$ $\sf (0{,}84x^2-14{,}63x+69{,}38)$.

1.5 Im Drachenviereck $\sf A_4B_4C_4D_4$ haben die Punkte $\sf A_4$ und $\sf C_4$ dieselbe Abszisse. Berechnen Sie den Flächeninhalt des Drachenvierecks $\sf A_4B_4C_4D_4$.

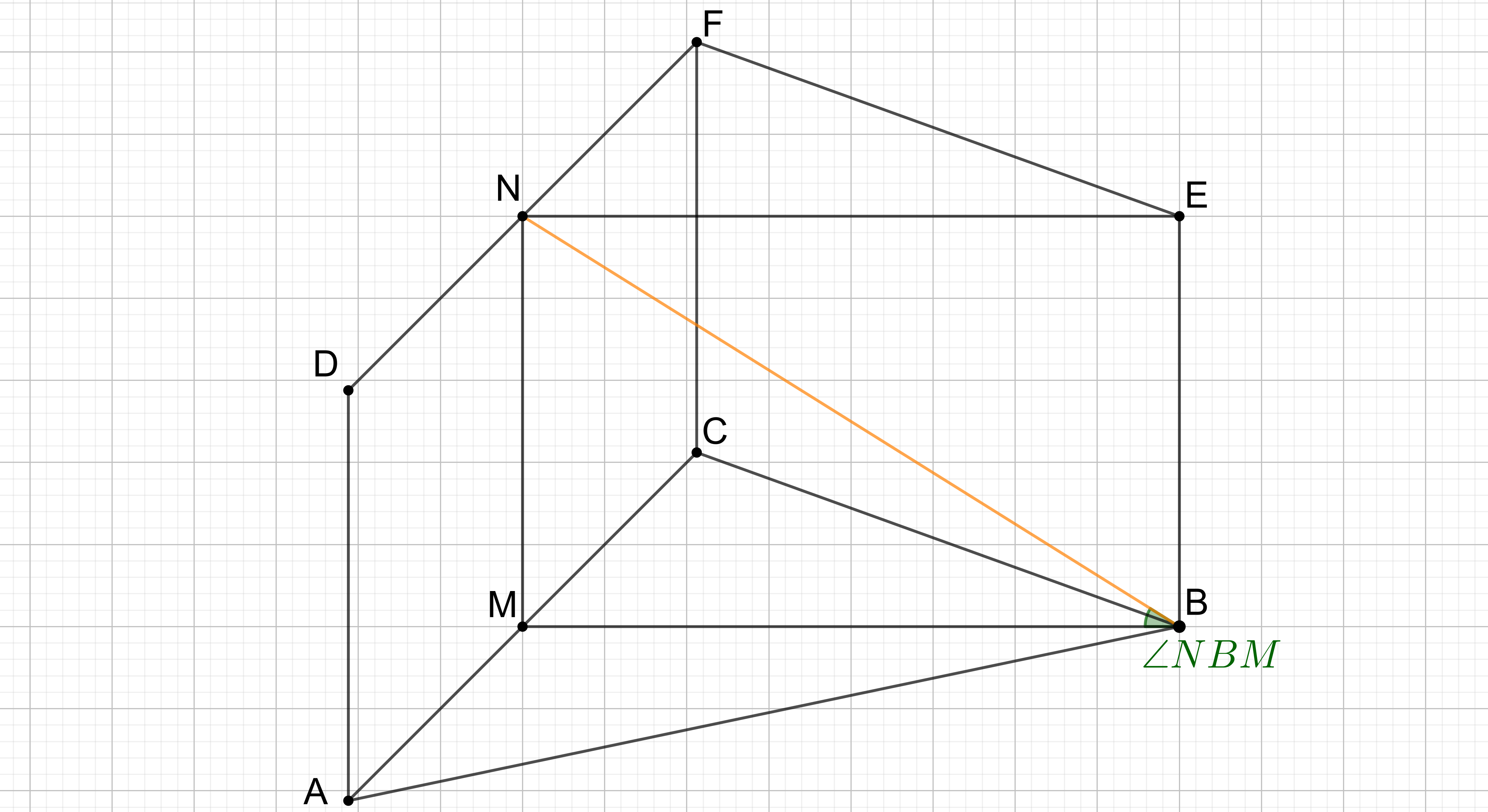
2.0 Das gleichschenklige Dreieck $\sf ABC$ ist die Grundfläche des geraden Prismas $\sf ABCDEF$. Der Punkt $\sf M$ ist der Mittelpunkt der Basis $\sf [AC]$. Der Punkt $\sf D$ liegt senkrecht über dem Punkt $\sf A$ und der Punkt $\sf N$ ist der Mittelpunkt der Strecke $\sf [DF]$. Es gilt: $\sf \overline{AC}=12\ \text{\sf cm};\overline{MB}=8\ \text{\sf cm};\overline{AD}=5\ \text{\sf cm}$.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

2.1 Zeichnen Sie das Schrägbild des Prismas $\sf ABCDEF$, wobei die Strecke $\sf [MB]$ auf der Schrägbildachse und der Punkt $\sf M$ links vom Punkt $\sf B$ liegen soll.

Für die Zeichnung gilt: $\sf q=\dfrac12;\ \omega=45^\circ$.

Zeichnen Sie sodann die Strecke $\sf [BN]$ ein und berechnen Sie das Maß des Winkels $\sf \angle NBM$.

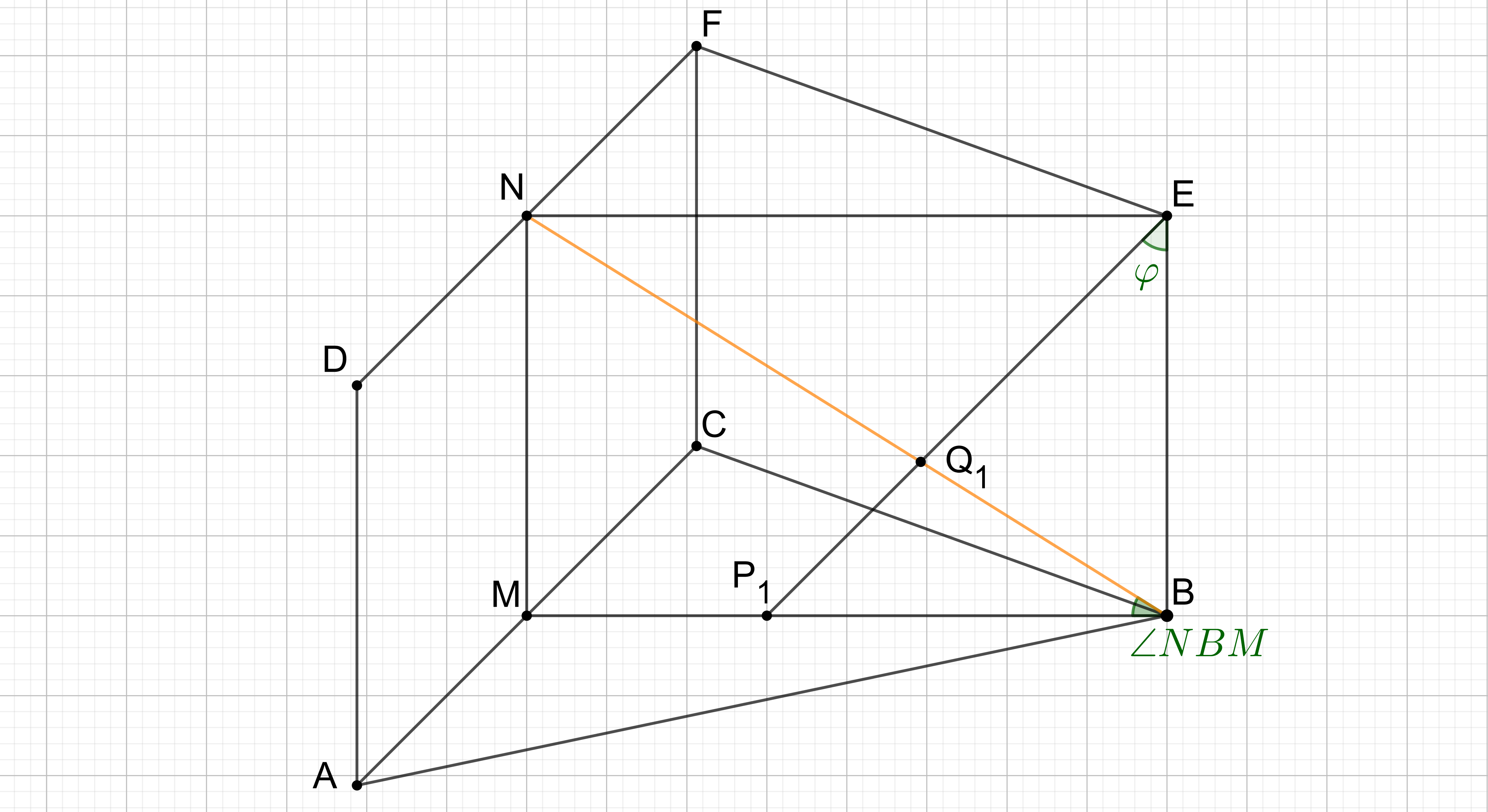
2.2 Punkte $\sf P_n$ liegen auf der Strecke $\sf [MB]$. Die Winkel $\sf P_nEB$ haben das Maß $\sf \varphi$ mit $\sf \varphi\in\rbrack\;0^\circ,57{,}99^\circ\rbrack$. Die Strecken $\sf [BN]$ und $\sf [EP_n]$ schneiden sich in Punkten $\sf Q_n$.

Zeichnen Sie für $\sf \varphi=45^\circ$ die Strecke $\sf [EP_1]$ und den Punkt $\sf Q_1$ in das Schrägbild zu 2.1 ein. Begründen Sie sodann rechnerisch die obere Intervallgrenze für $\sf \varphi$.

2.3 Zeigen Sie, dass für die Länge der Strecken$\sf [EQ_n]$ in Abhängigkeit von $\sf \varphi$ gilt:

Unter den Strecken $\sf [EQ_n]$ hat die Strecke $\sf [EQ_0]$ die minimale Länge. Berechnen Sie die Länge der Strecke $\sf [NQ_0]$.

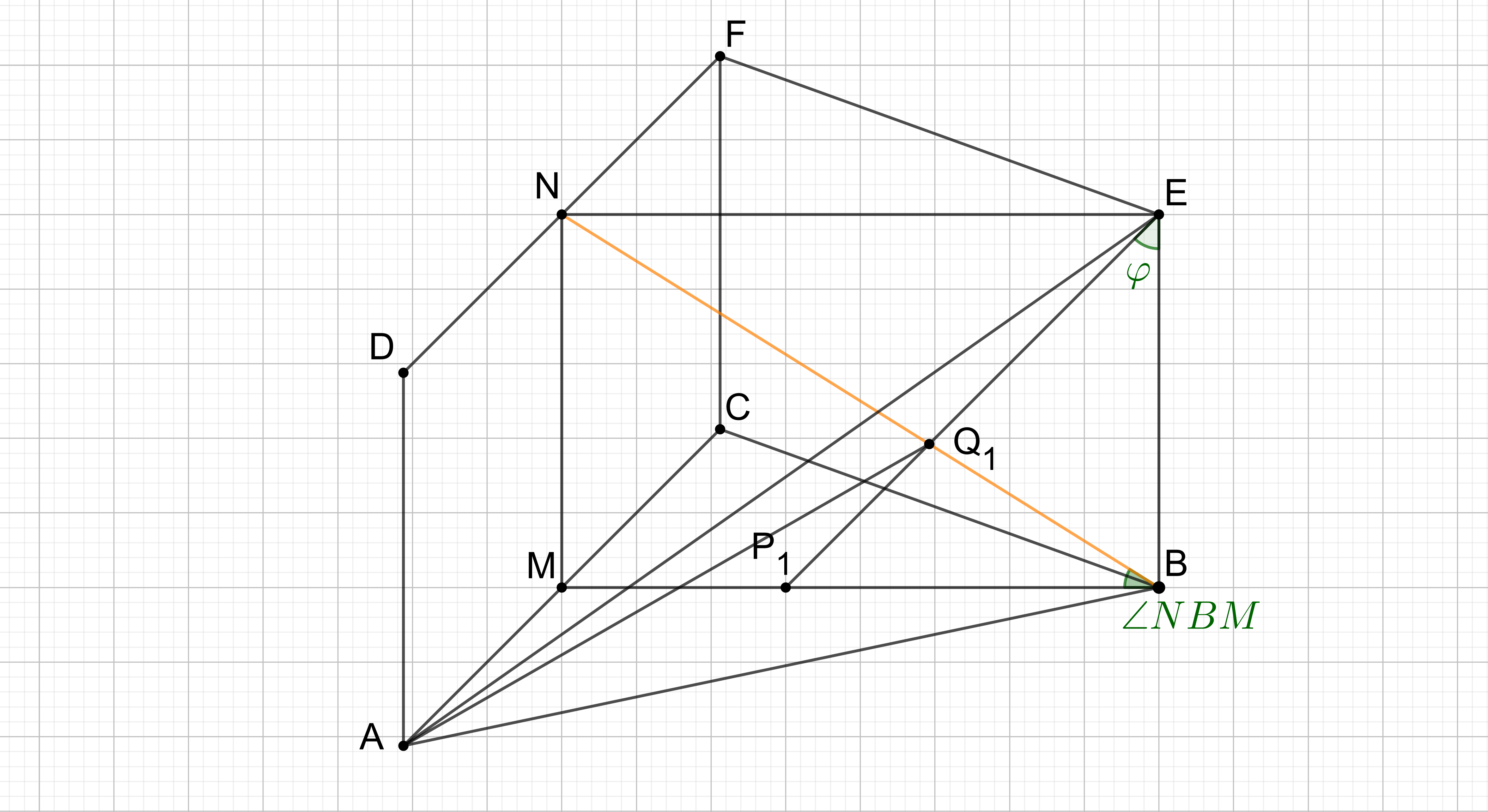
2.4 Der Punkt $\sf A$ ist die Spitze von Pyramiden $\sf Q_nBEA$ mit den Grundflächen $\sf Q_nBE$. Zeichnen Sie die Pyramide $\sf Q_1BEA$ in das Schrägbild zu 2.1 ein und ermitteln Sie sodann rechnerisch das Volumen $\sf V$ der Pyramiden $\sf Q_nBEA$ in Abhängigkeit von $\sf \varphi$.

[Ergebnis: $\sf V(\varphi)=\dfrac{21{,}2\cdot\sin\left(\varphi\right)}{\sin\left(\varphi+57{,}99^\circ\right)}\ \text{\sf cm}^3$]

2.5 Das Volumen der Pyramide $\sf Q_2BEA$ ist um $\sf 95\%$ kleiner als das Volumen des Prismas $\sf ABCDEF$. Berechnen Sie das zugehörige Maß für $\sf \varphi$.