Nachtermin Teil A - lernen mit Serlo!

Punkte $B_n$ auf der Geraden $g$ mit der Gleichung $y=-1{,}5$ und Punkte

$C_n(\textrm{x}|-0{,}25\cdot0{,}5^{\textrm{x}-4}+2)$ auf dem Graphen der Funktion $f$ mit der Gleichung

$\ y=-0{,}25\cdot0{,}5^{x-4}+2\$ haben dieselbe Abszisse $x\;(\mathbb{G}=\mathbb{R}\times\mathbb{R})$ . Sie bilden für $x>0{,}19$ zusammen mit dem Punkt $A(0|0)$ Dreiecke $AB_nC_n.$

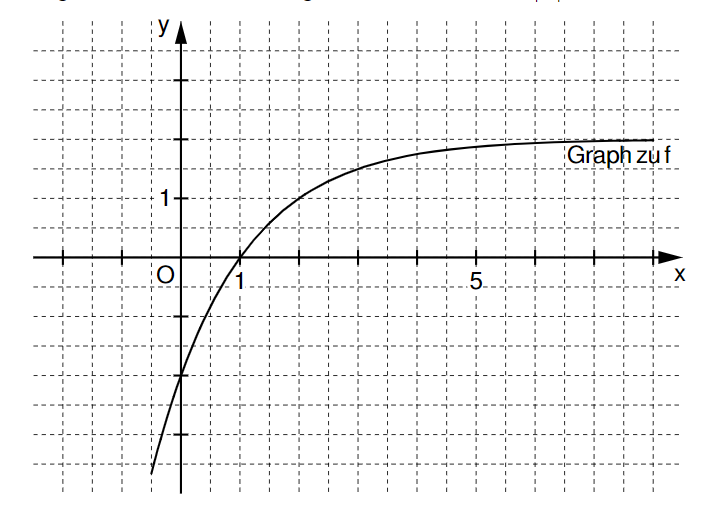
Im Koordinatensystem ist der Graph der Funktion $f$ bereits eingezeichnet.
Ergänzen Sie die Gerade $g$ und das Dreieck $AB_1C_1$ für $\textrm{x}=6$ .
Zeichnung der Gerade g und des Dreiecks $AB_nC_n$ für x = 6:
Zeichnung der Geraden g: $y=-1{,}5$ . Die Gerade (lineare Funktion) hat keine Steigung und schneidet die y-Achse bei $-1{,}5$ (rot).
Punkt $A (0|0)$ (blau).
Der Punkt $C_n(\textrm{x}|-0{,}25\cdot0{,}5^{\textrm{x}-4}+2)$ mit $x = 6$ :
$y\left(6\right)=-0{,}25\cdot0{,}5^{6-4}+2=-0{,}25\cdot0{,}5^2+2=-0{,}25\cdot0{,}25+2=\frac{31}{16}\approx1{,}94$
$C_1(6|1{,}94)$
$B_1$ und $C_1$ haben dieselbe Abszisse x und $B$ liegt auf der Geraden g: $x_B=6$ , $y_B=-1{,}5$
$\;\Rightarrow\;B_1(6|-1{,}5)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Unter den Dreiecken $AB_nC_n$ gibt es das gleichschenklige Dreieck $AB_2C_2$ mit der Basis $[B_2C_2]$ .

Bestimmen Sie rechnerisch die Koordinaten des Punktes $C_2$ .

Die Koordinaten des Punktes $C_2$ des gleichschenkligen Dreiecks $AB_2C_2$ :

Da die y-Koordinate des Punktes $B_n$ immer bei $y=-1{,}5$ liegt, suchen wir einen Punkt $B_n$ , der die y-Koordinate $y=1{,}5$ hat, nur dann ist das Dreieck $AB_2C_2$ mit Basis $[B_2C_2]$ gleichschenklig.

(Achtung: Am Ende der Aufgabe muss mit dem Logarithmus gerechnet werden.)

$\displaystyle y$	$=$	$\displaystyle -0{,}25\cdot0{,}5^{x-4}+2$
	↓	$y = 1{,}5$ setzen
$\displaystyle 1{,}5$	$=$	$\displaystyle −0{,}25⋅0{,}5x−4+2$	$\displaystyle -2$
$\displaystyle 1{,}5−2$	$=$	$\displaystyle -0{,}25\cdot0{,}5^{x-4}$
$\displaystyle -0{,}5$	$=$	$\displaystyle -0{,}25\cdot0{,}5^{x-4}$	$\displaystyle \cdot\left(-1\right)$
$\displaystyle 0{,}5$	$=$	$\displaystyle 0{,}25\cdot0{,}5^{x-4}$
	↓	Exponenten trennen
$\displaystyle 0{,}5$	$=$	$\displaystyle 0{,}25\cdot\frac{0{,}5^x}{0{,}5^4}$	$\displaystyle \cdot0{,}5^4$
$\displaystyle 0{,}5⋅0{,}54$	$=$	$\displaystyle 0{,}25\cdot0{,}5^x$
$\displaystyle 0{,}5^5$	$=$	$\displaystyle 0{,}25\cdot0{,}5^x$
	↓	Schreibe $0{,}25$ als $0{,}5^2$ .
$\displaystyle 0{,}5^5$	$=$	$\displaystyle 0{,}5^2\cdot0{,}5^x$	$\displaystyle :\left(0{,}5^2\right)$
$\displaystyle \frac{0{,}5^5}{0{,}5^2}$	$=$	$\displaystyle 0{,}5^x$
	↓	Seitenwechsel
$\displaystyle 0{,}5^x$	$=$	$\displaystyle 0{,}5^3$
$\displaystyle 0{,}5^x$	$=$	$\displaystyle 0{,}125$
$\displaystyle x$	$=$	$\displaystyle \log_{0{,}5}\left(0{,}125\right)$
$\displaystyle x$	$=$	$\displaystyle 3$

$\mathbb{L}=\left\{3\right\}$ und daraus folgt $C_2(3|1{,}5)$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇