Nachtermin Teil A - lernen mit Serlo!

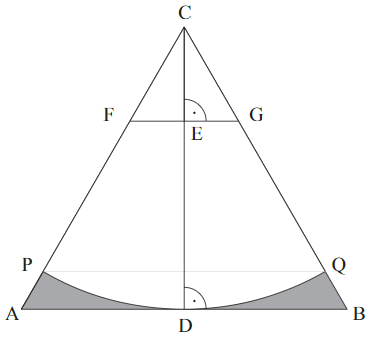
Die nebenstehende Skizze zeigt die gleichseitigen Dreiecke $ABC$ und $FGC$ mit den zugehörigen Höhen $[CD]$ und $[CE]$ .

Es gilt: $F\in\left[AC\right];\;G\in\left[BC\right];\; \left[AB\right]\ \parallel\left[FG\right];$

$\left[CD\right]\cap\left[FG\right]=\left\{E\right\};$

$\overline{CE}\ =2{,}3\cdot\sqrt{3}cm;\ \overline{DE}=2\cdot\overline{CE}.$

Berechnen Sie die Seitenlänge $a$ des gleichseitigen Dreiecks $ABC$ . $[$ Ergebnis: $a = 13{,}8 cm]$
Der Kreisbogen $\overset\frown{PQ}$ mit dem Mittelpunkt $C$ und dem Radius $\overline{CD}$ schneidet die Seite $[AC]$ im Punkt $P$ und die Seite $[BC]$ im Punkt $Q$ .
Berechnen Sie den Flächeninhalt $A$ der grau markierten Fläche, die durch die Strecken $[PA]$ , $[AB]$ , $[BQ]$ und den Kreisbogen $\overset\frown{PQ}$ begrenzt ist und ermitteln Sie sodann den prozentualen Anteil des Flächeninhalts $A$ am Flächeninhalt des Dreiecks $ABC$ .