Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgaben findest Du hier zum Ausdrucken als PDF.
- 1
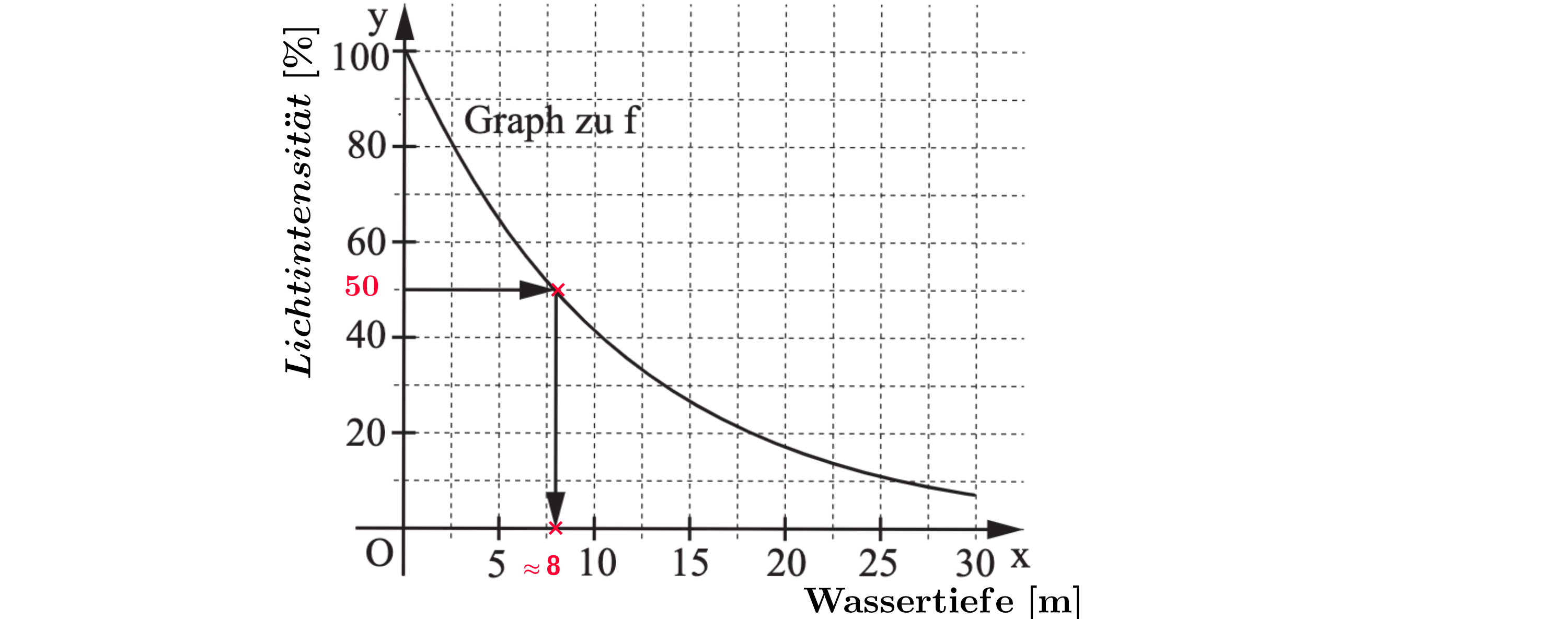
Die Intensität von Licht, das in einen See einfällt, nimmt prozentual mit zunehmender Wassertiefe ab. Eine Messung hat ergeben, dass sich in x Metern Wassertiefe die verbleibende Lichtintensität y Prozent näherungsweise durch die Funktion bestimmen lässt.
Geben Sie an, um wie viel Prozent die Lichtintensität nach der Funktion pro Meter Wassertiefe abnimmt.
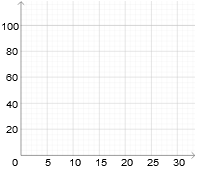
Ergänzen Sie die Wertetabelle auf Ganze gerundet und zeichnen Sie sodann den Graphen der Funktion in das Koordinatensystem ein.
x
0
2,5
5
10
15
20
25
30
Ermitteln Sie mithilfe des Graphen zu f, bei welcher Wassertiefe die Lichtintensität nur noch 50 % beträgt.
An einem anderen See wurde zur gleichen Zeit in 18 Meter Wassertiefe eine verbleibende Lichtintensität von 22 % gemessen. Überprüfen Sie durch Rechnung, ob an diesem See dieselben Bedingungen, wie in der Aufgabenstellung beschrieben, herrschen.
- 2
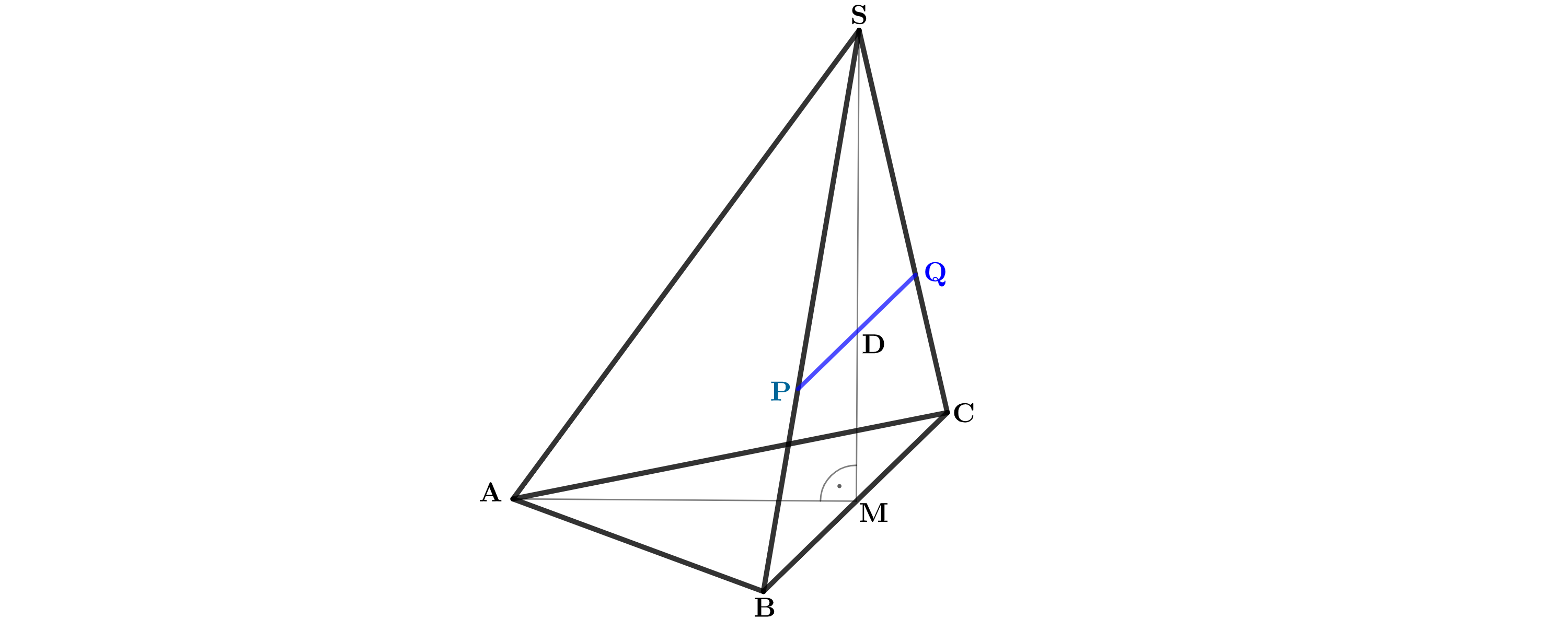
Das gleichschenklige Dreieck mit der Basis ist die Grundfläche der Pyramide . Die Spitze liegt senkrecht über dem Mittelpunkt der Basis (siehe Zeichnung). Es gilt: ; ; . Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
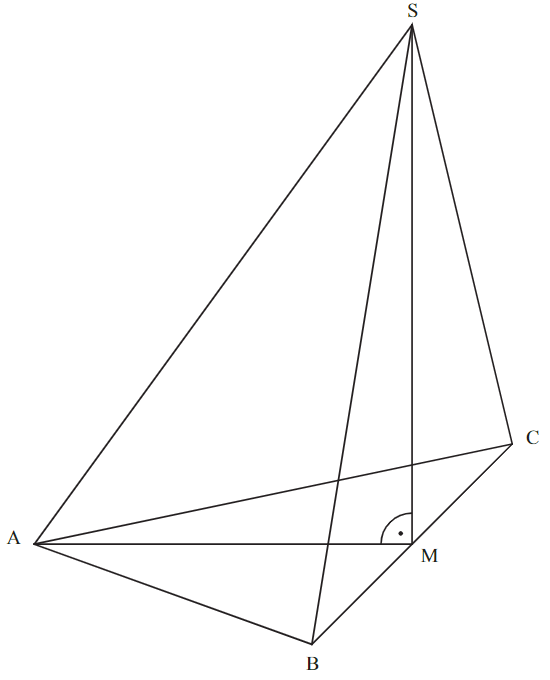
Berechnen Sie die Länge der Strecke und das Maß des Winkels . [Ergebnisse: ]
Die Strecke mit und ist parallel zur Strecke . Der Punkt ist der Mittelpunkt der Strecke mit . Zeichnen Sie die Strecke in das Schrägbild zur Aufgabenstellung ein und berechnen Sie deren Länge. [Ergebnis: ]
Punkte auf der Strecke mit cm bilden zusammen mit den Punkten und Dreiecke .
Zeichnen Sie das Dreieck für in das Schrägbild zur Aufgabenstellung ein und bestimmen Sie sodann durch Rechnung das Maß des Winkels .
[Teilergebnis: cm]
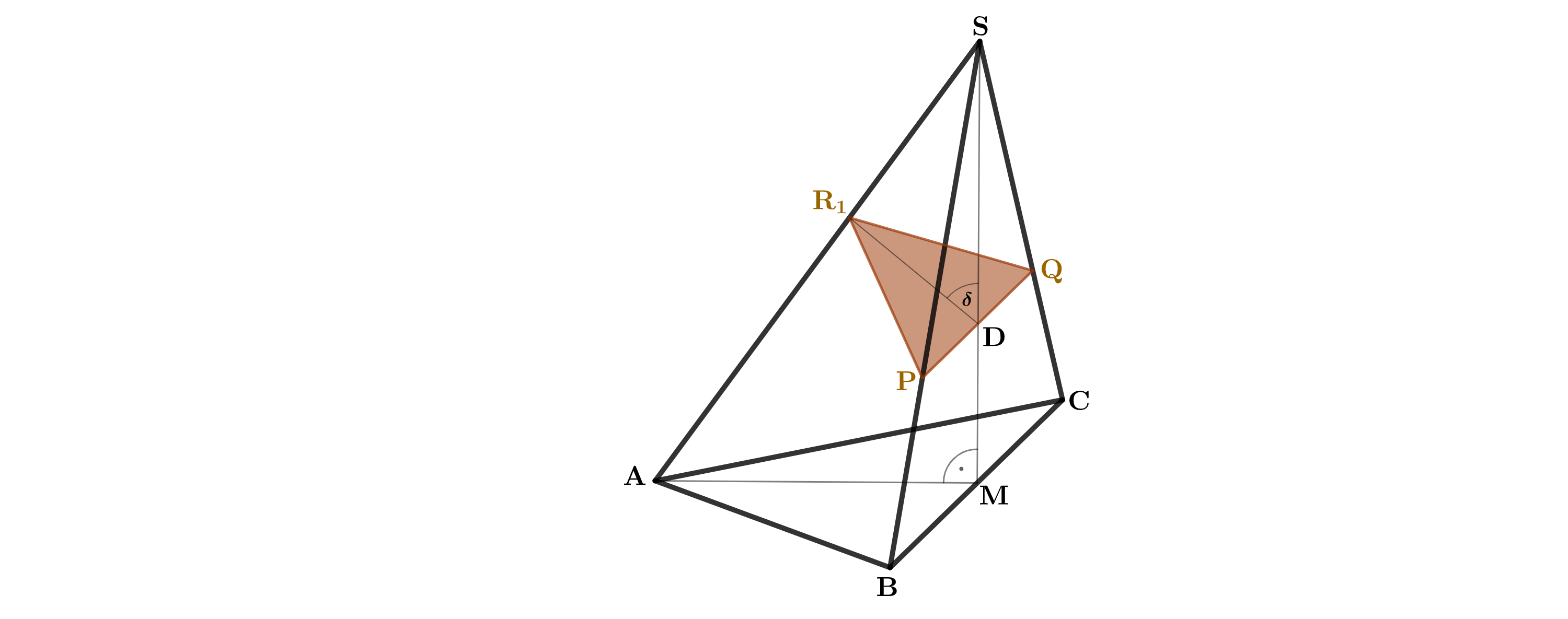
Das Dreieck ist die Grundfläche von Pyramiden .
Zeichnen Sie die Höhe der Pyramide mit dem Höhenfußpunkt in das Schrägbild zur Aufgabenstellung ein. Ermitteln Sie sodann die Länge der Strecken [] der Pyramiden in Abhängigkeit von .
- 3
Die nebenstehende Skizze zeigt die gleichseitigen Dreiecke und mit den zugehörigen Höhen und .
Es gilt:
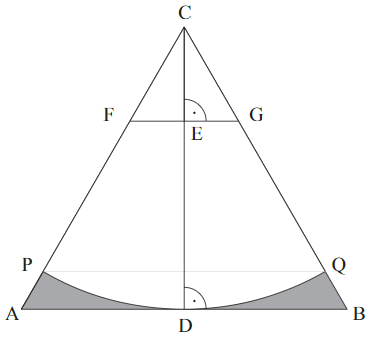
Berechnen Sie die Seitenlänge des gleichseitigen Dreiecks . Ergebnis:
Der Kreisbogen mit dem Mittelpunkt und dem Radius schneidet die Seite im Punkt und die Seite im Punkt .
Berechnen Sie den Flächeninhalt der grau markierten Fläche, die durch die Strecken , , und den Kreisbogen begrenzt ist und ermitteln Sie sodann den prozentualen Anteil des Flächeninhalts am Flächeninhalt des Dreiecks .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?