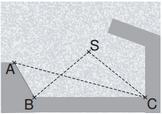
Teilaufgabe c

Diese Aufgabe löst du am besten durch Berechnung des Winkels $\measuredangle\mathrm{ACP}$ und danach durch Anwendung der Verhältnisse von Seitenlängen in einem rechtwinkligen Dreieck.

Den Winkel $\measuredangle\mathrm{ACP}$ erhältst du durch $\measuredangle\mathrm{ACP} = \measuredangle\mathrm{SCB} - \measuredangle\mathrm{ACB}$.

Dafür benötigst du $\measuredangle\mathrm{SCB}$. Diesen Winkel erhältst du durch den Sinussatz.

Unter Anwendung des Sinussatzes erhältst du:

$\dfrac{\sin(\measuredangle\mathrm{SCB})}{\overline{BS}} = \dfrac{\sin(\measuredangle\mathrm{CBS})}{\overline{SC}}$

und mit den eingesetzten Werten

$\dfrac{\sin(\measuredangle\mathrm{SCB})}{353\, \mathrm{m}} = \dfrac{\sin(38°)}{356\, \mathrm{m}}$

und damit ergibt sich

$\sin(\measuredangle\mathrm{SCB}) = \dfrac{\sin(38°)}{356\, \mathrm{m}} \cdot 353\, \mathrm{m}$

ausgerechnet und nach dem Winkel umgeformt, (Anwendung von $\sin^{-1}$) erhältst du dann 

$\measuredangle\mathrm{SCB} = 37{,}62°.$

Mithilfe von $\measuredangle\mathrm{SCB}$ und dem Sinus im rechtwinkligen Dreieck erhältst du in dem Dreieck $\Delta \mathrm{ACP}$ folgenden Ansatz:

$\sin(\measuredangle\mathrm{PCA}) = \dfrac{\overline{AP}}{\overline{AC}}.$

Dieser Ansatz basiert darauf, dass der kürzeste Weg der Strecke $\overline{AP}$ die senkrechte Verbindung von $A$ zur Strecke $\overline{SC}$ darstellt. Dies bedeutet, dass es sich bei dem Dreieck $\Delta \mathrm{ACP}$ um ein rechtwinkliges Dreieck handelt und du das Seitenverhältnis mit dem Sinus anwenden kannst.

Dabei ist $\measuredangle\mathrm{PCA}=\measuredangle\mathrm{ACP} = \measuredangle\mathrm{SCB} - \measuredangle\mathrm{ACB}=37{,}52°-16°=21{,}62°$.

Umgeformt erhältst du mit dem Ansatz 

${\overline{AP}} = \sin(\mathrm{21{,}62°}) \cdot 635\, \mathrm{m}$

also ${\overline{AP}} = 234\, \mathrm{m}.$

Teilaufgabe a

Diese Aufgabe kannst du mit Hilfe des Kosinussatzes lösen.

Betrachte das Dreieck $\Delta \mathrm{ABC}$.

Die Seite $\overline{\mathrm{BC}}$ liegt dem Winkel $\measuredangle \mathrm{BAC}$ gegenüber. Laut Kosinussatz gilt daher:

$\overline {\mathrm{BC}}^2=\overline {\mathrm{AB}}^2+\overline {\mathrm{AC}}^2-2\cdot \overline {\mathrm{AB}} \cdot \overline {\mathrm{AC}} \cdot \cos \measuredangle \mathrm{BAC}$

Wenn du die Zahlenwerte einsetzt, heißt das:

$\overline{\mathrm{BC}}^2 = (182 \ \mathrm{m})^2 + (635 \ \mathrm{m})^2 - 2\cdot (182 \ \mathrm{m})\cdot (635 \ \mathrm{m})\cdot \cos 58°$

Daraus erhältst du $\overline{\mathrm{BC}}$ ganz einfach durch Wurzelziehen und Ausrechnen mit dem Taschenrechner:

$\def\arraystretch{1.25} \begin{array}{rcl} \overline{\mathrm{BC}}&=& \sqrt{(182 \, \mathrm{m})^2 + (635 \, \mathrm{m})^2 - 2\cdot (182 \, \mathrm{m})\cdot (635 \, \mathrm{m})\cdot \cos 58°}\\ &=&\sqrt{33124\, \mathrm{m^2} + 403225\,\mathrm{m^2} - (231140\cdot \cos58°)\mathrm{m^2}}\\ &=&\sqrt{(436349-231140\cdot \cos 58°)\,\mathrm{m^2}}\\ &\approx&\sqrt{313863{,}461265\,\mathrm{m^2}}\\ &\approx&560\,\mathrm{m} \end{array}$

Teilaufgabe b

Auch diese Aufgabe kannst du mithilfe des Kosinussatzes lösen.

Davor rechnest du aber am besten noch die Winkel $\measuredangle\mathrm{CBA}$und $\measuredangle \mathrm{CBS}$ aus.

$\measuredangle\mathrm{CBA}$ erhältst du durch die Winkelsumme in Dreiecken, indem du ausnutzt, dass

$180° = \measuredangle\mathrm{CBA}+ \measuredangle\mathrm{BAC} + \measuredangle\mathrm{ACB}$

Umgeformt erhältst du 

$\measuredangle\mathrm{CBA}=180°-\measuredangle\mathrm{BAC}-\measuredangle\mathrm{ACB}^{ }$

und damit

$\measuredangle\mathrm{CBA} = 180° - 58° - 16°$

also:

$\measuredangle\mathrm{CBA} = 106°$

Wegen $\measuredangle\mathrm{CBA}= \measuredangle\mathrm{CBS}+\measuredangle\mathrm{SBA}$ erhältst du $\measuredangle\mathrm{CBS}$ durch

$\measuredangle\mathrm{CBS} = \measuredangle\mathrm{CBA} - \measuredangle\mathrm{SBA}$

Damit ergibt sich, 

$\measuredangle\mathrm{CBS} = 106° - 68°$

also $\measuredangle\mathrm{CBS} = 38°$.

Mit dem Winkel $\measuredangle\mathrm{CBS}$ kannst du den Kosinussatz anwenden, um $\overline{\mathrm{SC}}$ zu bestimmen:

$\overline{\mathrm{SC}} = \sqrt{\overline{\mathrm{BS}}^2 + \overline{\mathrm{BC}}² - 2 \cdot \overline{\mathrm{BS}}\cdot \overline{\mathrm{BC}} \cdot \cos(\measuredangle\mathrm{CBS})}$

$\overline{\mathrm{SC}} = \sqrt{{(353\, \mathrm{m})}² + {(560\, \mathrm{m})}² - 2 \cdot 353\, \mathrm{m}\cdot 560\, \mathrm{m} \cdot \cos(38°)}$

und damit erhältst du $\overline{\mathrm{SC}} = 356\, \mathrm{m}.$