Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Die Skizze zeigt den Grundriss eines Hafenbeckens. Ein Schiff befindet sich an der Position .
Es gilt:
Runden Sie im Folgenden auf ganze Meter.
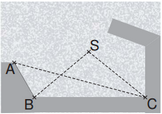
Berechnen Sie die Länge der Strecke . Ergebnis:
Bestimmen Sie durch Rechnung, wie weit die Position vom Punkt entfernt ist.
Teilergebnis: Ergebnis:
Das Schiff entfernt sich von , bis es die Position erreicht. liegt auf der Halbgeraden [ und hat die kleinstmögliche Entfernung zum Punkt .
Berechnen Sie die Länge der Strecke .
- 2

Punkte für Aufgabe 2.3: 2 P
Punkte für Aufgabe 2.4: 2 P
- 3
Die nachfolgende Skizze zeigt den Axialschnitt eines Rotationskörpers mit der Rotationsachse und dient als Vorlage für eine Lampe, die aus einer Plexiglasscheibe und einem Lampenschirm besteht.
Es gilt: ; ; ; ; .
Für den Durchmesser des Halbkreisbogens gilt:
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
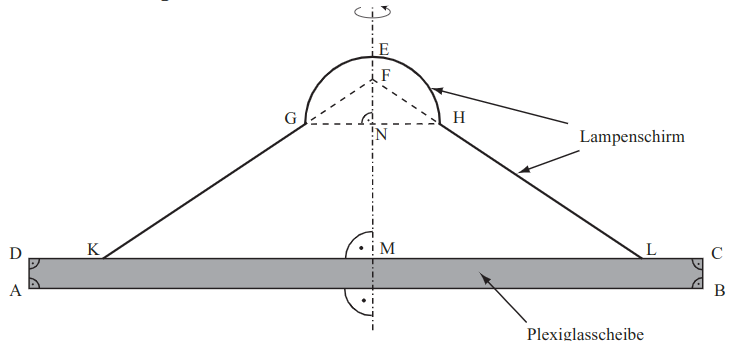
Berechnen Sie das Volumen der Plexiglasscheibe.
Ermitteln Sie rechnerisch den Inhalt der Außenfläche des Lampenschirms.
- 4
Gegeben sind die Parabel mit und die Gerade mit
Zeigen Sie durch Rechnung, dass sich die Gleichung der Parabel auf die Form bringen lässt und zeichnen Sie die Parabel für und die Gerade in das Koordinatensystem ein.
Punkte auf der Geraden und Punkte auf der Parabel haben dieselbe Abszisse und sind Eckpunkte von Rechtecken mit .
Zeichnen Sie das Rechteck für das in das Koordinatensystem zu Teilaufgabe (a) ein.
Berechnen Sie die Länge der Seiten der Rechtecke in Abhängigkeit von der Abszisse der Punkte und ermitteln Sie sodann rechnerisch den Umfang der Rechtecke . Ergebnis:
Die Rechtecke und haben einen Umfang von .
Berechnen Sie die zugehörigen Werte für .
Um wie viel Prozent nimmt der Flächeninhalt der Rechtecke aus Teilaufgabe (b) zu, wenn man die Seitenlänge verdoppelt?
Kreuzen Sie an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?