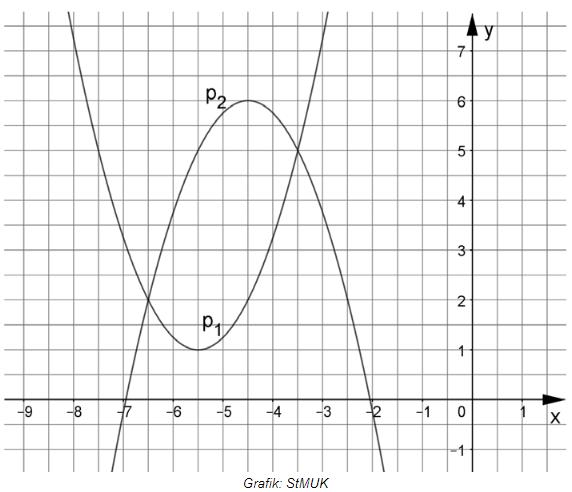
Lösen Sie die folgenden Aufgaben.
Berechnen Sie die Funktionsgleichung der Parabel in der Normalform
Überprüfen Sie rechnerisch, ob die Punkte und auf der Parabel liegen.
Bestimmen Sie die Funktionsgleichung der Parabel in der Scheitelpunktform und geben Sie den Scheitelpunkt an.
Ermitteln Sie rechnerisch die Koordinaten der Schnittpunkte und der beiden Parabeln und .
ZeichnenSie die Parabeln und in ein Koordinatensystem mit der Längeneinheit .
Der Scheitelpunkt einer nach unten geöffneten Parabel liegt im dritten Quadranten. Diese Parabel wird erst an der -Achse und dann an der -Achse gespiegelt.
Beschreiben Sie nachvollziehbar, in welchem Quadranten der Scheitelpunkt der so entstandenen Parabel liegt, und in welche Richtung die Parabel geöffnet ist.