Teil B-Aufgabengruppe I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier sind die originalen Aufgabenstellungen zu finden.
- 1
Lösen Sie die folgenden Aufgaben.
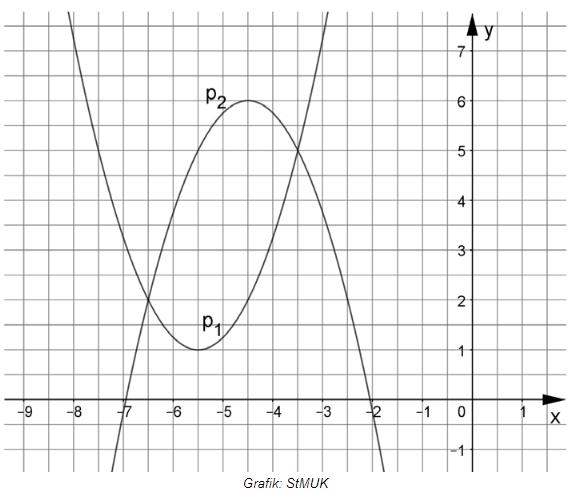
Berechnen Sie die Funktionsgleichung der Parabel in der Normalform
Überprüfen Sie rechnerisch, ob die Punkte und auf der Parabel liegen.
Bestimmen Sie die Funktionsgleichung der Parabel in der Scheitelpunktform und geben Sie den Scheitelpunkt an.
Ermitteln Sie rechnerisch die Koordinaten der Schnittpunkte und der beiden Parabeln und .
ZeichnenSie die Parabeln und in ein Koordinatensystem mit der Längeneinheit .
Der Scheitelpunkt einer nach unten geöffneten Parabel liegt im dritten Quadranten. Diese Parabel wird erst an der -Achse und dann an der -Achse gespiegelt.
Beschreiben Sie nachvollziehbar, in welchem Quadranten der Scheitelpunkt der so entstandenen Parabel liegt, und in welche Richtung die Parabel geöffnet ist.
- 2
Folgende Gleichungen sind Anwendungen von binomischen Formeln. Stellen Sie die vollständigen Gleichungen auf und notieren Sie diese auf Ihrem Lösungsblatt.
- 3
Lösen Sie die folgenden Aufgaben.
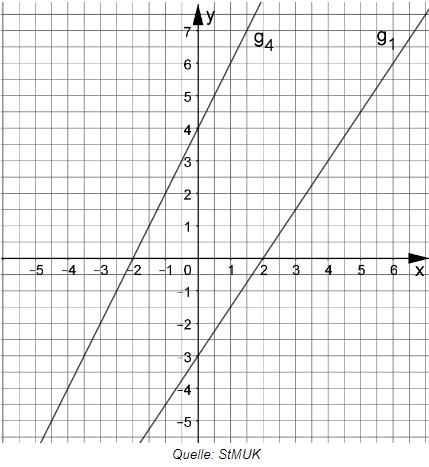
Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden , die durch die Punkte und verläuft.
Die Gerade mit der Funktionsgleichung steht senkrecht auf der Geraden .
Berechnen Sie zu einer möglichen Geraden die Funktionsgleichung in der Normalform und beschreiben Sie Ihr Vorgehen in Worten.
Gegeben ist die Gerade mit der Funktionsgleichung
ist der Schnittpunkt der Geraden mit der -Achse.
Bestimmen Sie rechnerisch die -Koordinate dieses Punktes und geben Sie an.
Zeichnen Sie die Geraden und in ein Koordinatensystem mit der
Längeneinheit .
Begründen Sie in Worten, warum diese beiden Geraden sich schneiden.
Berechnen Sie den spitzen Winkel, den die Gerade mit der -Achse einschließt.
- 4
Geben Sie die Definitionsmenge der folgenden Gleichung an und ermitteln Sie rechnerisch die Lösungsmenge.
- 5
Eine Hohlkugel mit einem Außendurchmesser von soll als Dekoration für einen Baumarkt verwendet werden. Sie besteht aus Holz und hat eine Wandstärke von .
Die Hohlkugel erhält außen einen farbigen Anstrich.
Berechnen Sie den zu streichenden Oberflächeninhalt.
Die Hohlkugel soll von einem Kran auf das Dach des Baumarktes gehoben werden.
Berechnen Sie die Masse der Hohlkugel, wenn ein Kubikmeter des verwendeten Holzes wiegt.
- 6
In der folgenden Skizze stehen die drei parallelen Geraden g, h, und f
senkrecht auf der Geraden e.
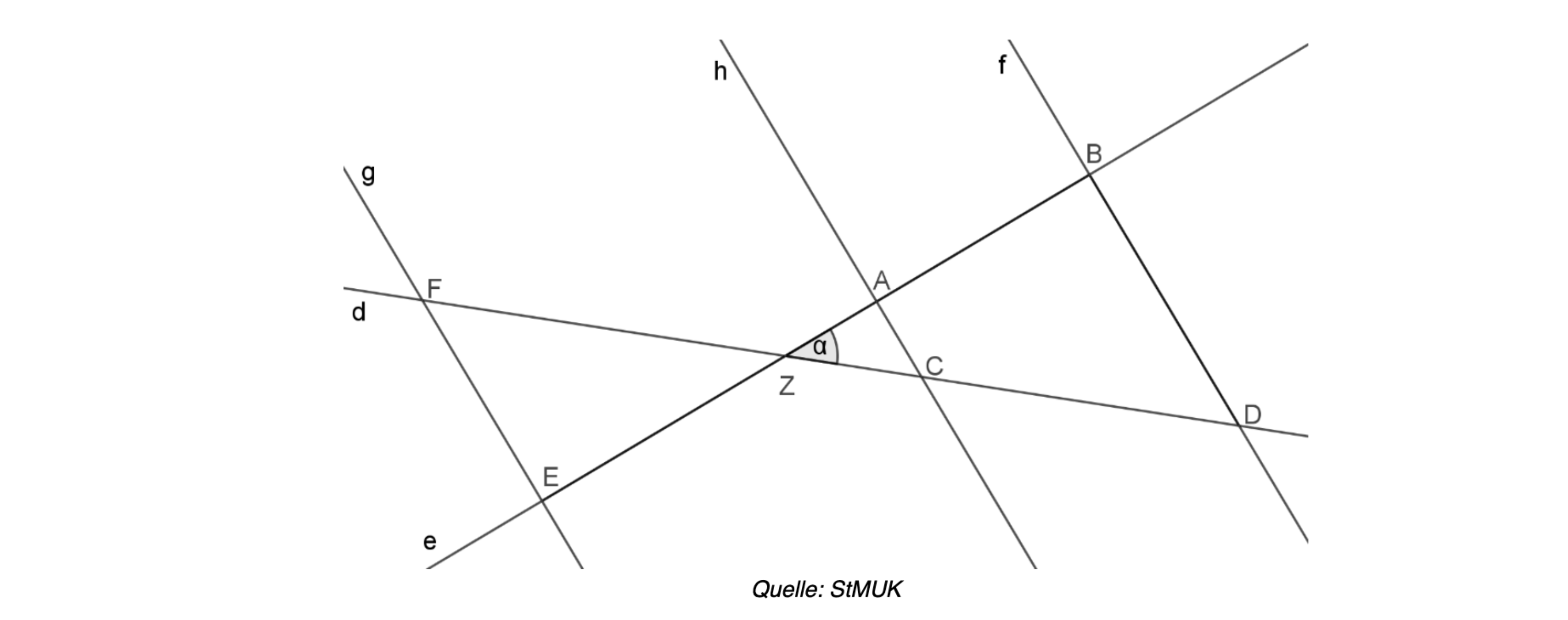
Die folgenden Aussagen sind richtig oderfalsch.
Berichtigen Sie die falschen Aussagen und begründen Sie die richtigen.
- 7
Frau Müller legt an und erhält einen jährlichen Zinssatz von .
Berechnen Sie für diesen Fall die Höhe des Kapitals nach einem Anlagezeitraum von vier Jahren.
Ermitteln Sie rechnerisch, nach wie vielen Jahren sich das Kapital bei diesem
Zinssatz von verdreifacht.
Berechnen Sie den jährlichen Zinssatz in Prozent, wenn das Kapital von 1000 € innerhalb von fünf Jahren auf 1160 € anwächst.
- 8
In einer Tüte befinden sich eine blaue, sieben rote und vier grüne Schokoladenkugeln.
Karl nimmt nacheinander nach dem Zufallsprinzip jeweils eine Kugel heraus
und isst sie sofort.
Bestimmen Sie die Wahrscheinlichkeit in Prozent, dass die ersten beiden
entnommenen Kugeln die gleiche Farbe haben.
Entscheiden Sie, ob es möglich ist, dass die elfte entnommene Schokoladenkugel blau ist.
Begründen Sie Ihre Antwort.
- 9
Berechnen Sie die Fläche des Dreiecks . Es gilt: cm und cm
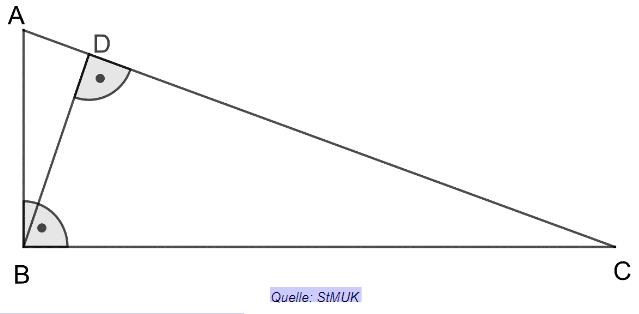
Hinweis: Skizze nicht maßstabsgetreu.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?