Teil B-Aufgabengruppe I - lernen mit Serlo!

Lösen Sie die folgenden Aufgaben.

Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden $g_{1}$ , die durch die Punkte $A (- 1 | - 4,5)$ und $B (4 | 3)$ verläuft.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Allgemeine Geradengleichung: $g_{1} (x) = m_{1} \cdot x + t_{1}$
$m$ bezeichnet die Steigung der Geraden und $t$ den y-Achsenabschnitt.
Steigung berechnen
Berechne zunächst die Steigung: $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ .
$m_{1} = \frac{3 - (- 4,5)}{4 - (- 1)} = \frac{7,5}{5} = 1,5$
$g_{1} (x) = 1,5 \cdot x + t_{1}$
y-Achsenabschnitt $t_{1}$ bestimmen
Setze nun z.B. den Punkt $B (4 | 3)$ in die Gleichung ein.
$3 = 1,5 \cdot (4) + t_{1}$
$t_{1} = 3 - 6 = - 3$
$g_{1} (x) = 1,5 \cdot x - 3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Steigung der Gerade mit der Formel $m = \frac{b_{2} - a_{2}}{b_{1} - a_{1}}$ .
Setze die berechnete Steigung in die Gleichung einer allgemeinen Gerade $g (x) = m x + t$ ein.
Setze einen Punkt $A$ oder $B$ ein und bestimme $b$ .
Die Gerade $g_{3}$ mit der Funktionsgleichung $0,5 y = 2,5 + x$ steht senkrecht auf der Geraden $g_{2}$ .
Berechnen Sie zu einer möglichen Geraden $g_{2}$ die Funktionsgleichung in der Normalform und beschreiben Sie Ihr Vorgehen in Worten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zwei zueinander senkrechte Geraden (analytische Geometrie)
$g_{3} : y = 2 x + 5$
$m_{2} = - \frac{1}{m_{3}}$
$m_{2} = - \frac{1}{2} = - 0,5$
Wähle einen beliebigen Achsenabschnitt für $g_{2}$ , z.B. $t_{2} = 2$ .
$g_{2} : y = - 0,5 x + 2$
Zusammenfassung:
Umformung der Geraden $g_{3}$ , durch Division durch 0,5. Bestimmung der Steigung mithilfe der Steigung von $g_{3}$ . Wahl eines Achsenabschnitts. Aufstellung der Gleichung in der Normalform.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Steigung von $g_{2}$ und wähle einen Achsenabschnitt.
Gegeben ist die Gerade $g_{4}$ mit der Funktionsgleichung $y = 2 x + 4 .$
$N_{4}$ ist der Schnittpunkt der Geraden $g_{4}$ mit der $x$ -Achse.
Bestimmen Sie rechnerisch die $x$ -Koordinate dieses Punktes und geben Sie $N_{4}$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
$g_{4}$ : $y = 2 x + 4$
Setze die Geradengleichung $0$ .
$0 = 2 x + 4$
$x = - 2$
$N_{4} (- 2 | 0)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zur Bestimmung des Schnittpunktes mit der $x$ -Achse setze $y = 0$ .
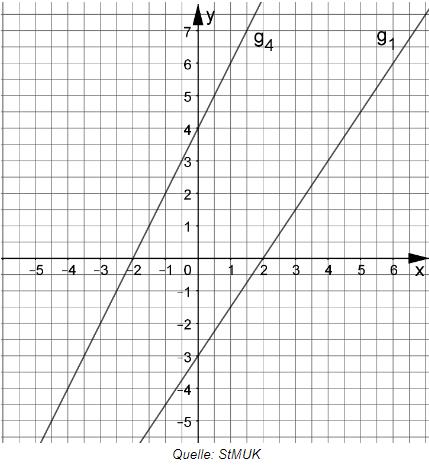
Zeichnen Sie die Geraden $g_{1}$ und $g_{4}$ in ein Koordinatensystem mit der
Längeneinheit $1 c m$ .
Begründen Sie in Worten, warum diese beiden Geraden sich schneiden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Geraden im Koordinatensystem
Die beiden Geraden schneiden sich, weil sie nicht parallel sind.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Skizziere die Geraden in das Koordinatensystem.
Skizziere dazu den Punkt, in dem die Gerade die y-Achse schneidet.
Verwende ein Steigungsdreieck, um die angegebene Steigung der Geraden im Koordinatensystem abzubilden.
Vergleiche die Abstände zwischen den Geraden und entscheide, ob sie parallel sind oder nicht.
Berechnen Sie den spitzen Winkel, den die Gerade $g_{1}$ mit der $x$ -Achse einschließt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung und Steigungswinkel
$g 1 : y = 1,5 x - 3$
$m = \tan (α)$
$1,5 = \tan (α)$
$α = \tan^{- 1} (1,5)$
$α \approx 56 °$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Verwende die Steigung der Geraden und Tangens, um die Größe des Winkels zu berechnen.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Steigung berechnen

y-Achsenabschnitt t1 bestimmen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

y-Achsenabschnitt $t_{1}$ bestimmen