Hilfsmittelfreier Teil - lernen mit Serlo!

Aufgabe 3

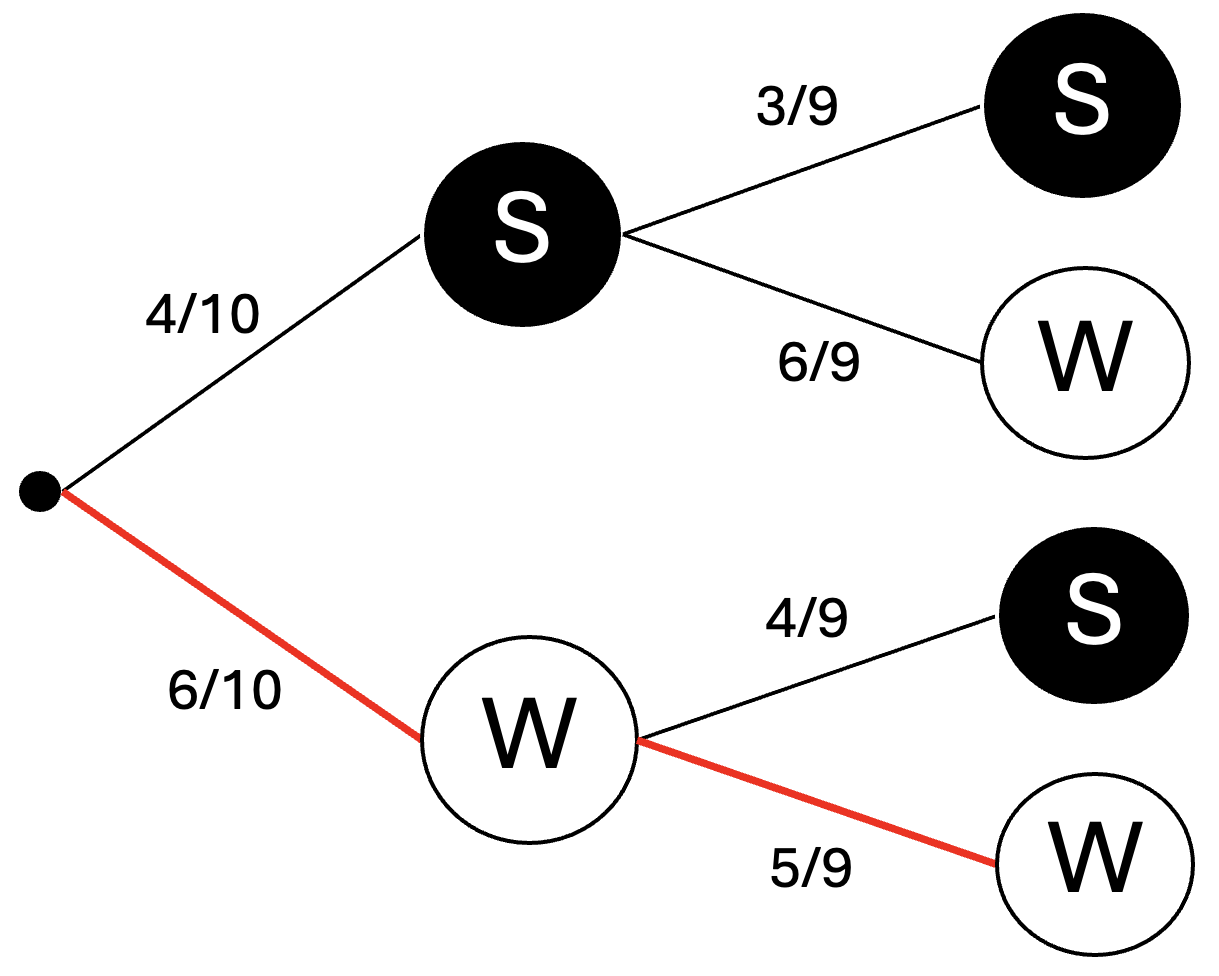
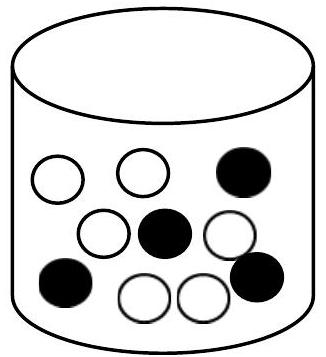
In einer Urne liegen 6 weiße und 4 schwarze Kugeln.

Dorothee zieht zweimal ohne Hinzusehen eine Kugel.

Die Kugeln werden nicht zurückgelegt.

Berechne die Wahrscheinlichkeit für das Ziehen von zwei weißen Kugeln.
Gib dein Ergebnis in Prozent an. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Baumdiagramm erstellen
Dorothee hat beim ersten Ziehen zwei Möglichkeiten: Entweder sie zieht eine schwarze oder eine weiße Kugel. Von insgesamt 10 Kugeln, sind...
... 4 schwarz, d.h. die Wahrscheinlichkeit liegt bei $\frac{4}{10}$
... 6 weiß, d.h. die Wahrscheinlichkeit liegt bei $\frac{6}{10}$
Zieht Dorothee beim ersten Mal eine schwarze Kugel, kann sie beim zweiten Zug ebenfalls eine schwarze oder eine weiße Kugel ziehen. Von den überbleibenden 9 Kugeln, sind...
... 3 schwarz, d.h. die Wahrscheinlichkeit liegt bei $\frac{3}{9}$
... 6 weiß, d.h. die Wahrscheinlichkeit liegt bei $\frac{6}{9}$
Zieht Dorothee beim ersten Mal eine weiße Kugel, bleiben wieder 9 Kugeln übrig. Davon sind...
... 4 schwarz, d.h. die Wahrscheinlichkeit liegt bei $\frac{4}{9}$
... 5 weiß, d.h. die Wahrscheinlichkeit liegt bei $\frac59$
Baumdiagramm
Wahrscheinlichkeit berechnen
Zum Berechnen der Wahrscheinlichkeit, zwei schwarze Kugeln hintereinander zu ziehen, interessiert uns der rot hinterlegte Pfad.
Wir wenden die Pfadregel an, multiplizieren also die Pfade miteinander:
$\text{P(w,w)}=\frac{6}{10}\cdot \frac{5}{9}=\frac{6\cdot5}{10\cdot 9}=\frac{30}{90}=\frac{1}{3}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Erstelle zunächst ein Baumdiagramm und beschrifte die Pfade mit Wahrscheinlichkeiten.
Untersuche, welche Kombination für die Aufgabenstellung relevant ist und berechne hierfür die Wahrscheinlichkeit.
Achtung: Die Kugeln werden nach dem Ziehen nicht zurückgelegt. Was bedeutet das für die Wahrscheinlichkeiten?

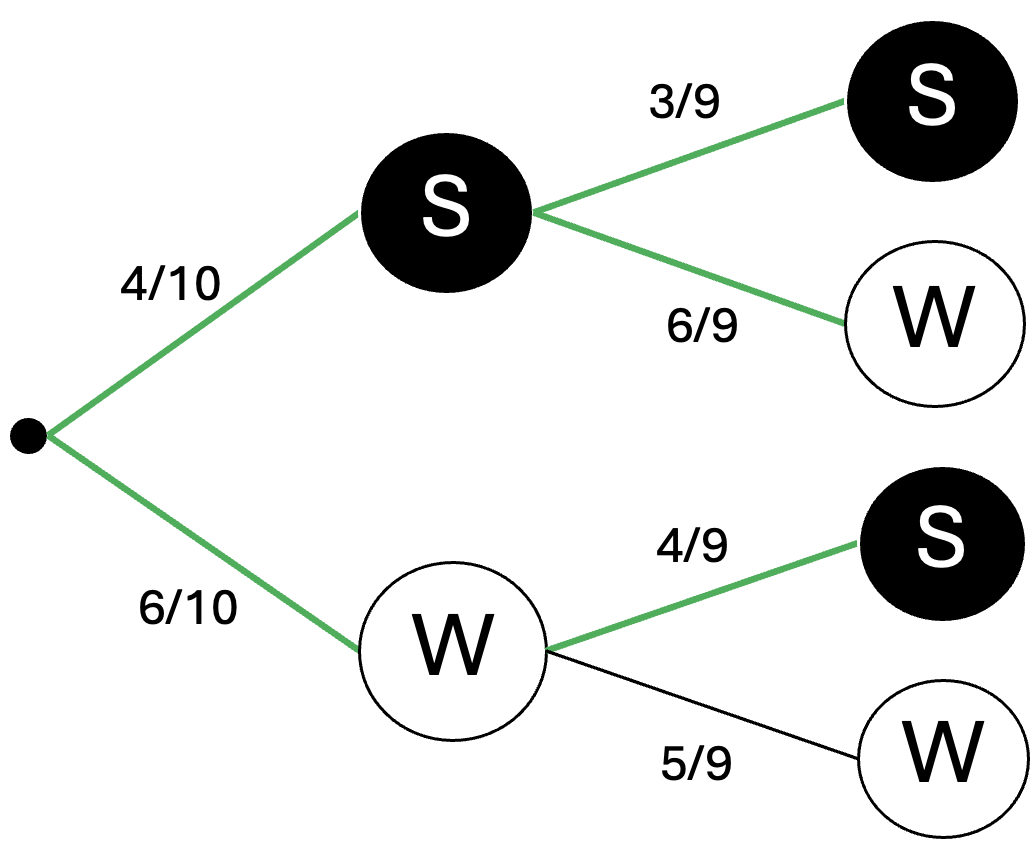
Berechne die Wahrscheinlichkeit, dass Dorothee mindestens eine schwarze Kugel zieht. (2 BE)

In einer anderen Urne befinden sich blaue und gelbe Kugeln.
Insgesamt sind es 10 Kugeln.
Wenn man aus dieser Urne zwei Kugeln ohne Zurücklegen zieht, dann beträgt die Wahrscheinlichkeit für zwei blaue Kugeln $\frac{2}{9}$ .
Hanke möchte die Anzahl an blauen Kugeln herausfinden und stellt eine Gleichung auf:
$\frac{x}{10} \cdot \frac{x-1}{9}=\frac{2}{9}$
Erkläre Hankes Gleichung. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Was wird hier berechnet?
Hier werden Brüche miteinander multipliziert, was auf die Pfadregel hindeutet:
$\dfrac{\text{x}}{10}$ beschreibt den 1. Zug
$\dfrac{\text{x}-1}{9}$ beschreibt den 2. Zug
Wofür stehen die beiden Brüche?
Hanke interessiert die Anzahl an blauen Kugeln, dafür steht die Variable x.
$\dfrac{\color{lightblue}\text{x}}{\color{orange}10}$ steht also für die Wahrscheinlichkeit, von insgesamt 10 Kugeln beim 1. Zug eine blaue Kugel zu ziehen
Betrachtet man nun den 2. Zug: $\dfrac{\color{lightblue}\text{x}-1}{\color{orange}9}$
Da die Kugel nach dem ersten Zug nicht zurückgelegt wird, sind nur noch insgesamt 9 Kugeln in der Urne.
Hanke zieht beim ersten Zug eine blaue Kugel, d.h. in der Urne befinden sich nicht mehr x blaue Kugeln sondern eine weniger, also $\color{lightblue}\text{x}-1$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bevor du dir die Zahlen genau ansiehst: Erkläre die Funktion der Rechnung. Wofür multipliziert man zwei Wahrscheinlichkeiten in einem Baumdiagramm?
Analysiere die beiden Brüche. Beschreibe, was sich verändert und warum.

$\displaystyle \text{P(mindestens eine schwarze Kugel)}$	$=$	$\displaystyle \text{P(s, s)}+\text{P(s, w)}+\text{P(w, s)}$
	↓	Pfadregel: Multiplikation der Pfade
	$=$	$\displaystyle (\frac{4}{10}\cdot\frac{3}{9})+(\frac{4}{10}\cdot\frac{6}{9})+(\frac{6}{10}\cdot\frac{4}{9})$
	$=$	$\displaystyle \frac{12}{90}+\frac{24}{90}+\frac{24}{90}$
	$=$	$\displaystyle \frac{60}{90}$
	$=$	$\displaystyle \frac{2}{3}$

Aufgabe 3

Baumdiagramm erstellen

Wahrscheinlichkeit berechnen

Hast du eine Frage oder Feedback?

Baumdiagramm aus a

Wahrscheinlichkeit berechnen:

Hast du eine Frage oder Feedback?

Was wird hier berechnet?

Wofür stehen die beiden Brüche?

Hast du eine Frage oder Feedback?