Hilfsmittelfreier Teil
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Aufgaben zu Prüfung IGS E 2021, Hilfsmittelfreier Teil. Zum Download hier.
- 1
Aufgabe 1
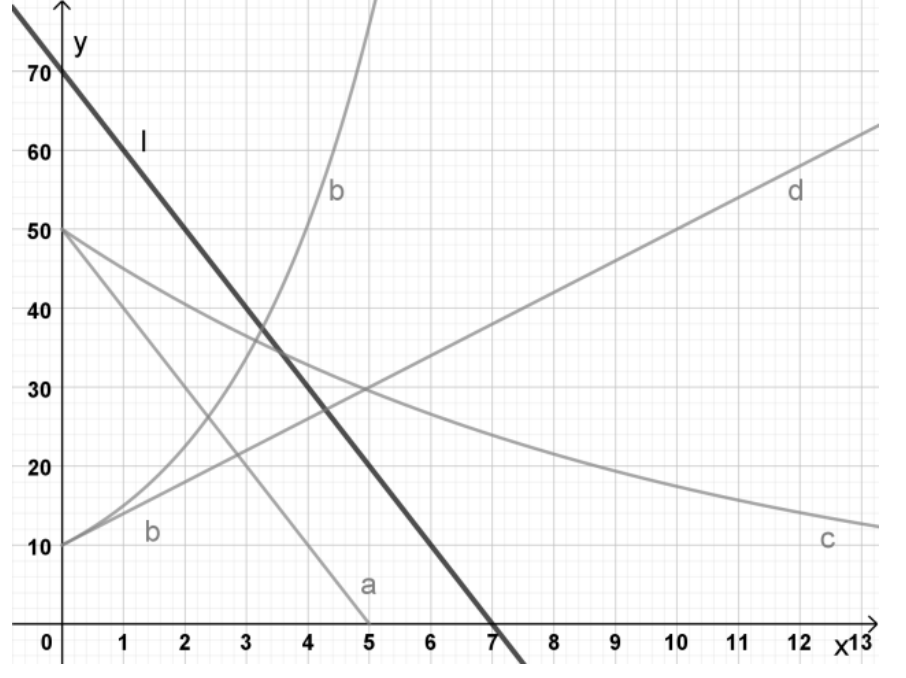
Ordne jedem der folgenden Texte den zugehörigen Graphen und eine passende Funktionsgleichung zu. (4 BE)
Du kannst die Objekte anklicken und mit der Maus ziehen.
Begründe deine Zuordnungen des Graphen zu Text III.
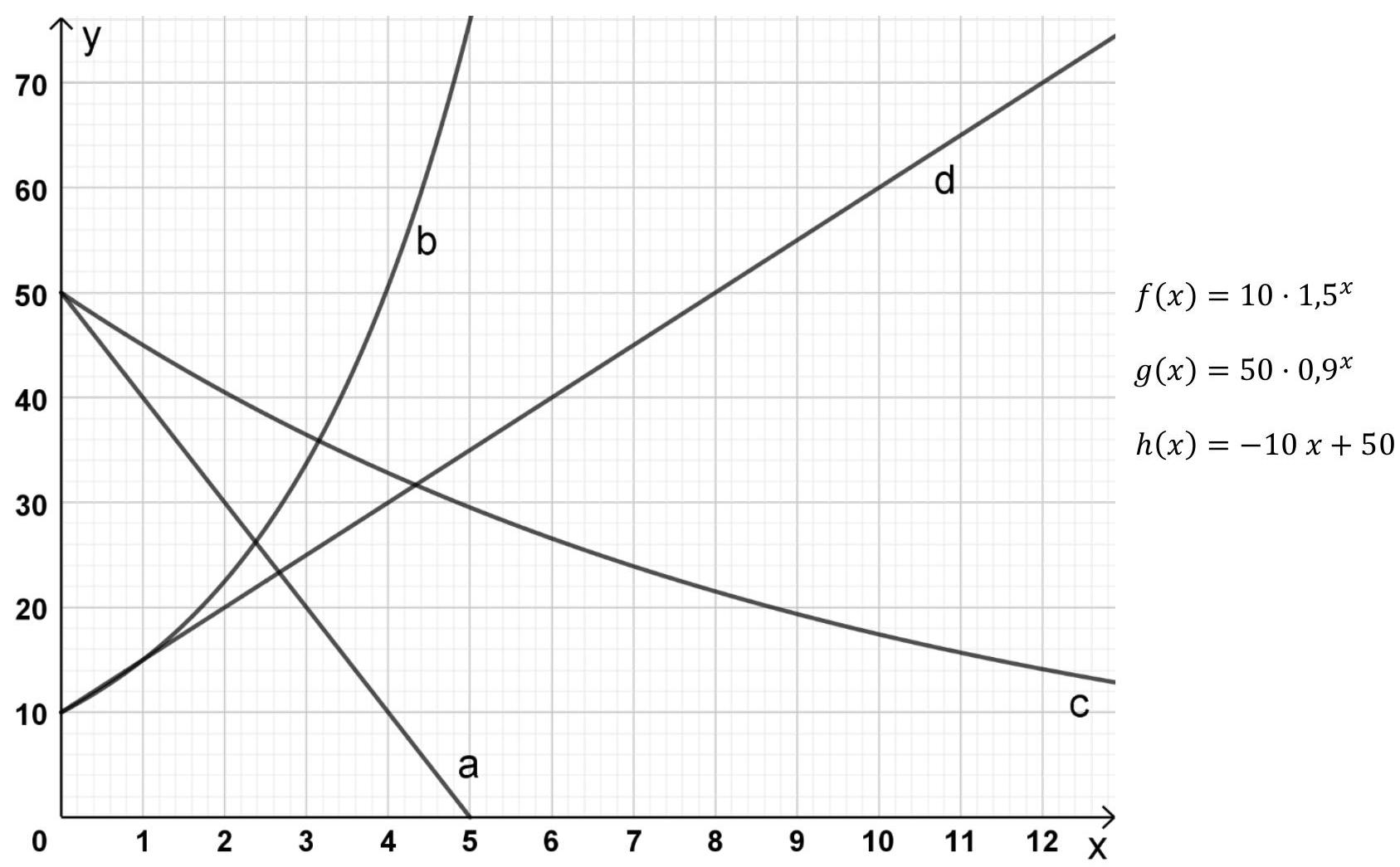
Gegeben ist die Funktion mit .
Zeichne den Graphen zu der Funktion in das Koordinatensystem. (2 BE)
Begründe, weshalb die Graphen der Funktionen und parallel sind. (1 BE)
- 2
Aufgabe 2
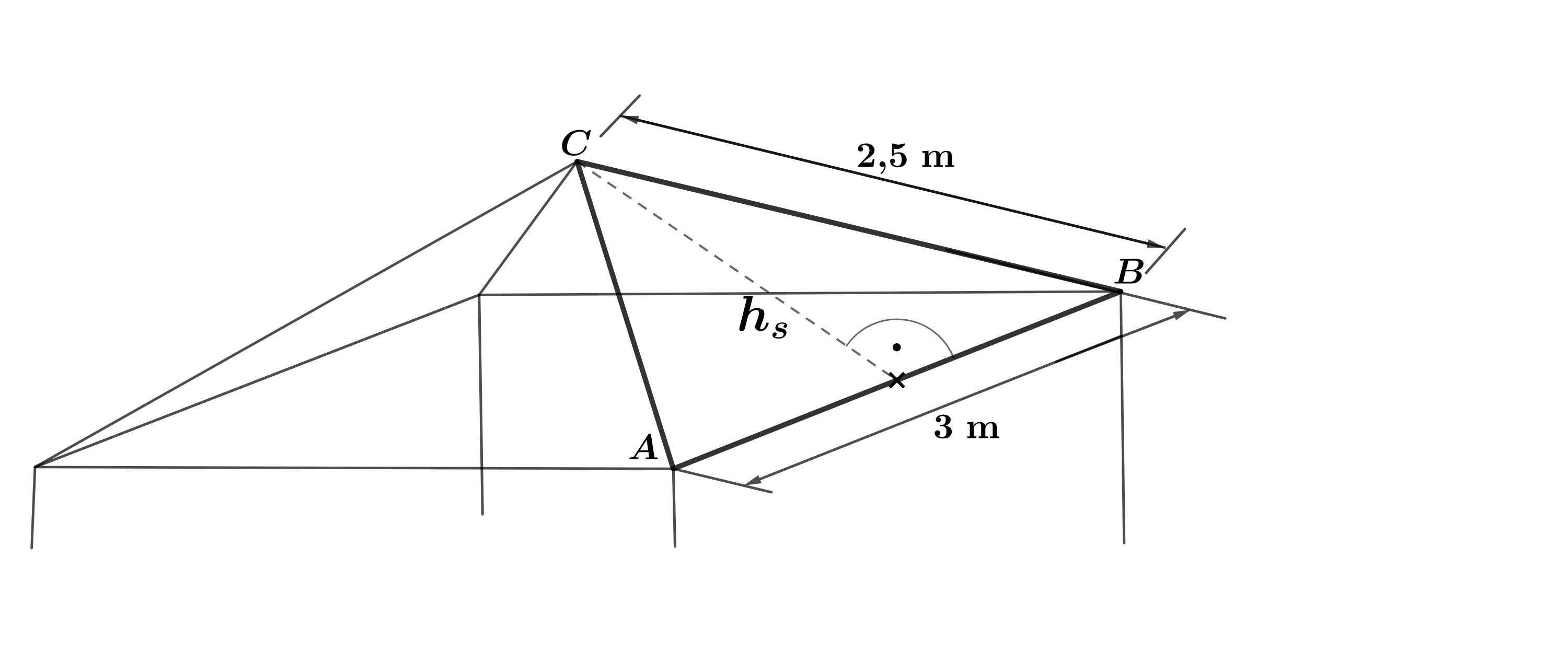
Der abgebildete Pavillon besteht aus einem Quader und einer Pyramide.
Der Quader hat eine quadratische Grundfläche.
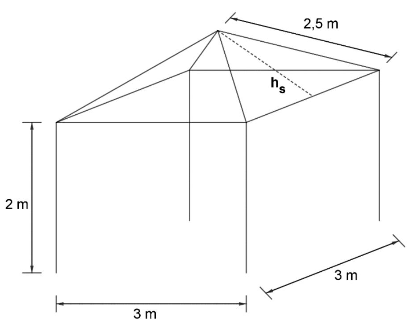

Die Skizze zeigt die Stangen des Pavillons.
Berechne die Gesamtlänge aller Stangen. (2 BE)
Berechne die Höhe eines Dreiecks der Pyramide. (2 BE)
Der Pavillon ist teilweise von Planen bedeckt. Die Planen bedecken vereinfacht betrachtet die vier schrägen Dachflächen und zwei Seiten des Quaders.
Berechne den gesamten Flächeninhalt der Planen. (2 BE)
(Wenn du b) nicht gelöst hast, verwende .)
- 3
Aufgabe 3
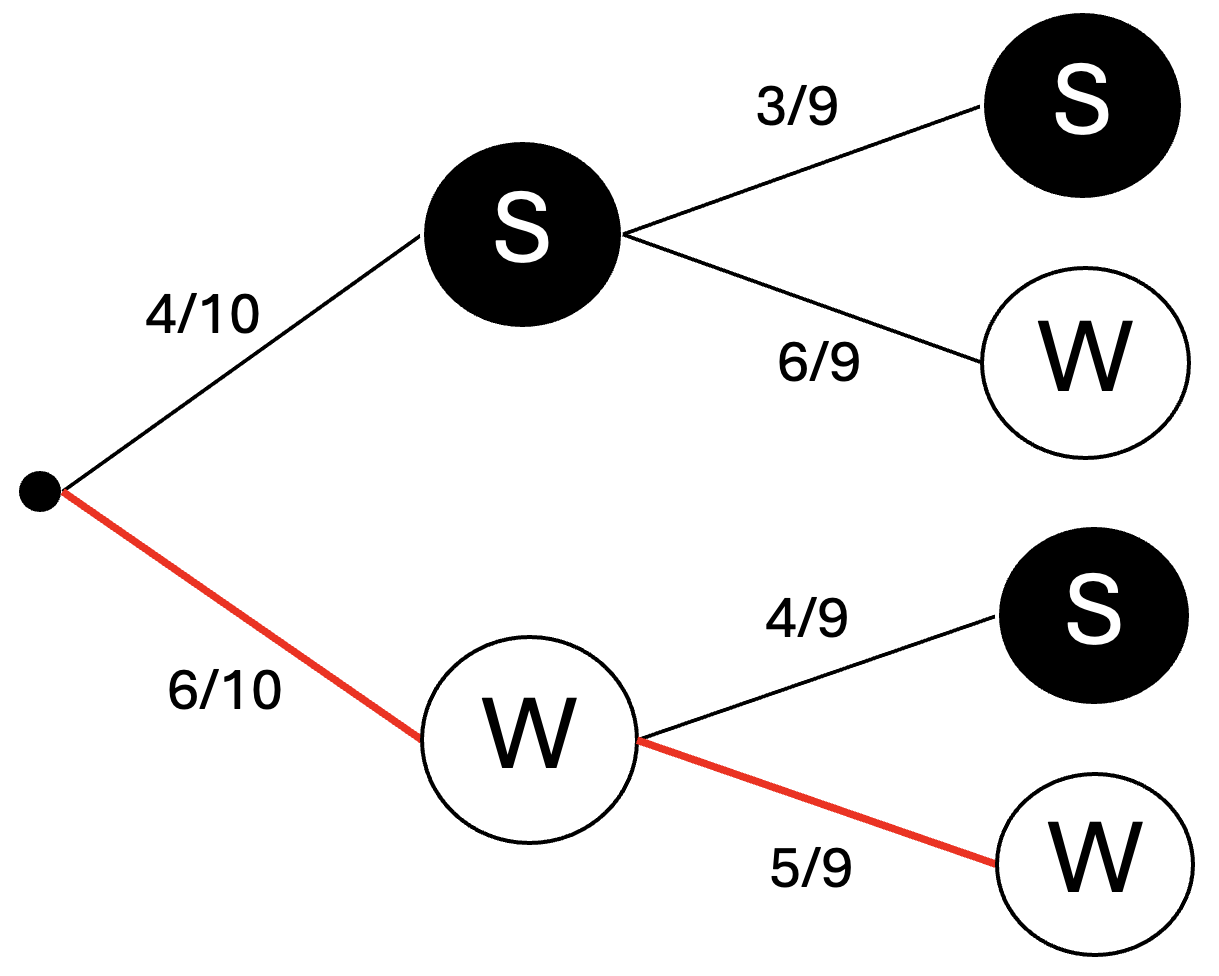
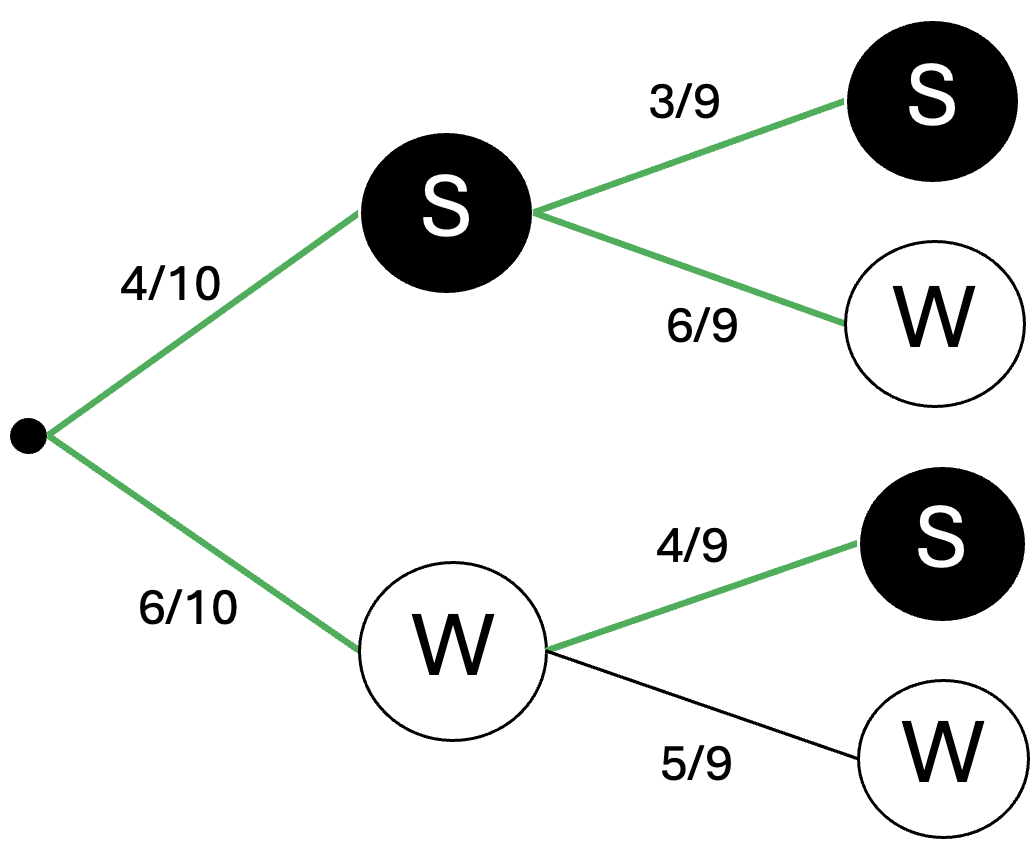
In einer Urne liegen 6 weiße und 4 schwarze Kugeln.
Dorothee zieht zweimal ohne Hinzusehen eine Kugel.
Die Kugeln werden nicht zurückgelegt.
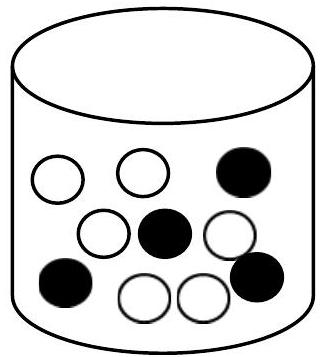
Berechne die Wahrscheinlichkeit für das Ziehen von zwei weißen Kugeln.
Gib dein Ergebnis in Prozent an. (3 BE)
Berechne die Wahrscheinlichkeit, dass Dorothee mindestens eine schwarze Kugel zieht. (2 BE)
In einer anderen Urne befinden sich blaue und gelbe Kugeln.
Insgesamt sind es 10 Kugeln.
Wenn man aus dieser Urne zwei Kugeln ohne Zurücklegen zieht, dann beträgt die Wahrscheinlichkeit für zwei blaue Kugeln .
Hanke möchte die Anzahl an blauen Kugeln herausfinden und stellt eine Gleichung auf:
Erkläre Hankes Gleichung. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?