Prüfungsteil 2 2022 - lernen mit Serlo!

Aufgabe 3: Parabel und Rechteck

Julia zeichnet mithilfe einer Geometriesoftware die Parabel $f$ mit der Funktionsgleichung $f(x)=-0{,}5 x^{2}+5{,}5$ in ein Koordinatensystem (Abbildung 1).

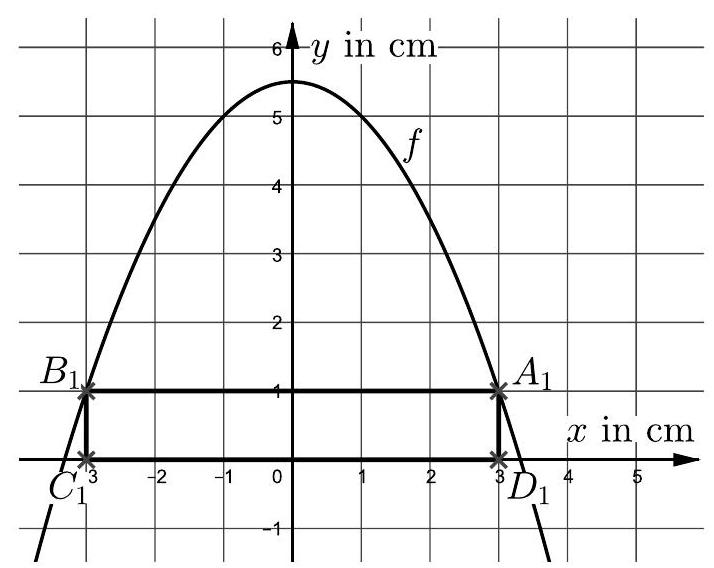
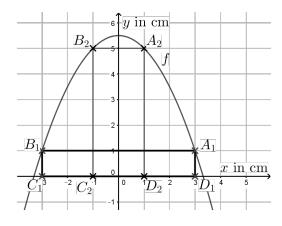
Abbildung 1: Parabel und Rechteck — Abbildung 1: Parabel $f$ und Rechteck $A_{1} B_{1} C_{1} D_{1}$

Bestätige durch eine Rechnung, dass der Punkt $A_{1}$ (3|1) auf der Parabel $f$ liegt. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Allgemeine Form und Scheitelform einer quadratischen Funktion
Nachweis
$f(x)=-0{,}5 x^{2}+5{,}5$
Setzte $x = 3$ in die Funktionsgleichung ein:
$f(3)=-0{,}5\cdot 3^2+5{,}5$
$f (3) = - 4,5 + 5,5$
$f (3) = 1$
Der Punkt $A_{1} = (3 ∣ 1)$ liegt auf der Parabel.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Setze die x-Koordinate des Punktes $A_{1}$ in die Funktionsgleichung ein und überprüfe, ob sich aus der Rechnung der richtige y-Wert ergibt.
Begründe mit den Eigenschaften dieser Parabel, dass der Punkt $B_{1}(-3 \mid 1)$ ebenfalls auf dem Graphen von $f$ liegt. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Begründung
Die Parabel ist achsensymmetrisch zur $y$ -Achse. Spiegelt man den Punkt $A_{1} (3 ∣ 1)$ an der $y$ -Achse, so erhält man den Punkt $B_{1} (- 3 ∣ 1)$ . Dieser liegt also ebenfalls auf dem Graphen von $f$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründe mithilfe der Symmetrie der Parabel.
Die Punkte $C_{1}$ und $D_{1}$ liegen auf der $x$ -Achse und bilden mit den Punkten $A_{1}$ und $B_{1}$ das Rechteck $A_{1} B_{1} C_{1} D_{1}$ .
Berechne den Umfang dieses Rechtecks. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Seitenlängen des Rechtecks
$U_{\text{Rechteck}}=2\cdot a+2\cdot b$
$a = 3 + 3 = 6$
$b = 1$
Umfang des Rechtecks
$U_{\text{Rechteck}}=2\cdot a+2\cdot b$
$U_{\text{Rechteck}}=12+2=14$
Der Umfang des Rechtecks beträgt $14 c m$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Seitenlängen des Rechtecks.
Berechne den Umfang des Rechtecks.
Ausgehend von anderen Punkten auf der Parabel $f$ kann man auf die gleiche Art weitere Rechtecke zeichnen.
(1) Zeichne den Punkt $A_{2}(1 \mid 5)$ in Abbildung 1 ein. (1 P)
(2) Ergänze die drei weiteren Punkte $B_{2}, C_{2}$ und $D_{2}$ und verbinde die vier Punkte zu dem Rechteck $A_{2} B_{2} C_{2} D_{2}$ . (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Koordinatensystem
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Julia stellt den Term (I) auf, mit dem man den Umfang für jedes dieser Rechtecke berechnen kann. Dazu nutzt sie die bekannte Formel zur Berechnung des Umfangs eines Rechtecks und erhält:
$\text { (I) } 2 \cdot 2 x+2 \cdot\left(-0{,}5 x^{2}+5{,}5\right) \text {. }$
Dabei ist $x > 0$ und steht für die $x$ -Koordinate des zum Rechteck gehörenden Punktes $A_{1}, A_{2}$ usw.
Begründe, dass mit dem Term (I) der Umfang jedes dieser Rechtecke berechnet werden kann. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Begründung
$U_{\text{Rechteck}}=2\cdot a+2\cdot b$
Die beiden waagrechten Rechtecksseiten sind jeweils $2 x$ lang.
Die beiden senkrechten Rechtecksseiten sind jeweils $-5x^2+5{,}5$ lang.
$U_{\text{Rechteck}}=2\cdot (2x)+2\cdot (-5x^2+5{,}5)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Stelle die Länge der Dreiecksseiten mit Hilfe der Unbekannten $x$ dar.
Stelle die Formel für den Umfang des Rechtecks mit diesen Rechteckseiten auf.
Julia vereinfacht den Term (I) zu (II) $-x^{2}+4 x+11$
Zeige durch Termumformungen, dass die beiden Terme (I) und (II) gleichwertig sind. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vereinfachen von Termen mit Klammern
Termumformung
$2 \cdot 2 x+2 \cdot\left(-0{,}5 x^{2}+5{,}5\right)$
$= 4 x - x^{2} + 11$
$= - x^{2} + 4 x + 11$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Klammer auf.
Sortiere nach den Exponenten.

Julia stellt die folgende Gleichung auf:

$-x^{2}+4 x+11=14{,}75$

(1) Löse die Gleichung. (3 P)

(2) Erkläre das Ergebnis in Bezug auf die Rechtecke unter der Parabel $f$ . (1 P)

Der Term (II) kann auch als Funktion $u$ mit $u(x)=-x^{2}+4 x+11$ interpretiert werden.

(1) Bestimme den Scheitelpunkt der Funktion $u$ (2 P) und

(2) erkläre seine Bedeutung für die Umfangsbetrachtung. (2 P)

$\displaystyle -x^2+4x+11$	$=$	$\displaystyle 14{,}75$	$\displaystyle -14{,}75$
$\displaystyle -x^2+4x-3{,}75$	$=$	$\displaystyle 0$	$\displaystyle \cdot\left(-1\right)$
$\displaystyle x^2-4x+3{,}75$	$=$	$\displaystyle 0$

$\displaystyle u\left(x\right)$	$=$	$\displaystyle -x^2+4x+11$	$\displaystyle +4-4$
	↓	quadratische Ergränzung
$\displaystyle u\left(x\right)$	$=$	$\displaystyle -x^2+4x-4+4+11$
	↓	(-1) ausklammmern und zusammenfassen
$\displaystyle u\left(x\right)$	$=$	$\displaystyle -\left(x^2-4x+4\right)+15$
	↓	2. Binomische Formel
$\displaystyle u\left(x\right)$	$=$	$\displaystyle -\left(x-2\right)^2+15$

Aufgabe 3: Parabel und Rechteck

Nachweis

Hast du eine Frage oder Feedback?

Begründung

Hast du eine Frage oder Feedback?

Seitenlängen des Rechtecks

Umfang des Rechtecks

Hast du eine Frage oder Feedback?

Skizze

Hast du eine Frage oder Feedback?

Begründung

Hast du eine Frage oder Feedback?

Termumformung

Hast du eine Frage oder Feedback?

Umformung der Gleichung

Lösung der Gleichung mit der Mitternachtsformel

Erklärung des Ergebnisses

Hast du eine Frage oder Feedback?

Scheitelform bestimmen

Beschreibung im Sachzusammenhang

Hast du eine Frage oder Feedback?