Teil 2, Stochastik I - lernen mit Serlo!

In einer bestimmten Region Deutschlands sind vier verschiedene Arten von DSL Internetanschlüssen verfügbar, wobei pro Haushalt nur genau eine der vier möglichen Anschlussarten gewählt werden kann. Die Tabelle veranschaulicht die Verteilung der verschiedenen Anschlüsse unter denjenigen Haushalten mit DSL-Anschluss:

Haushalte mit DSL 2000	Haushalte mit DSL 6000	Haushalte mit DSL 1600	Haushalte mit DSL 50000
17,3%	17,9%	19,8%	15%

Im Auftrag eines Internetdienstanbieters soll eine Umfrage zur Internetnutzung durchgeführt werden. Zu diesem Zweck werden 25 Haushalte der Region zufällig ausgewählt.

Berechnen Sie die Wahrscheinlichkeiten folgender Ereignisse:

$E_{4}$ : „Genau drei der ausgewählten Haushalte besitzen einen DSL 2000-Anschluss.“

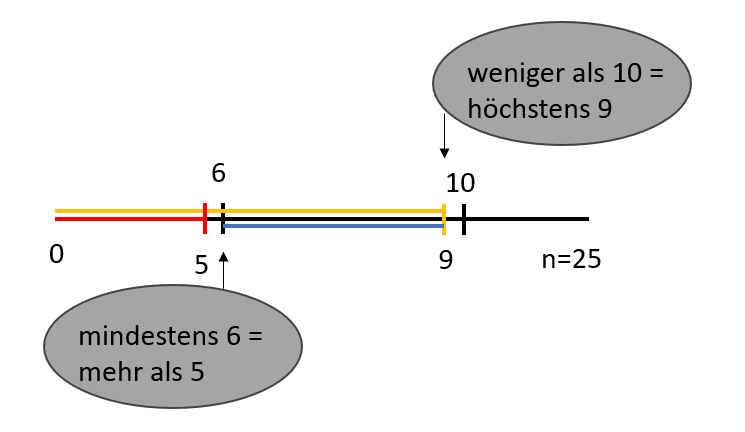
$E_{5}$ : „Mindestens sechs, aber weniger als zehn der ausgewählten Haushalte besitzen einen DSL 50000-Anschluss.“

$E_{6}$ : „Weniger als die Hälfte der ausgewählten Haushalte verfügen über einen DSLInternetanschluss.“

(6 BE)

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

	$P (6 \leq k < 10)$
	↓ Ersetze "weniger als 10" durch "höchstens 9"
$=$	$P (6 \leq k \leq 9)$
	↓ Die gesuchte Wahrscheinlichkeit kann als Differenz ausgedrückt werden. Da $k = 6$ aber in der kumulierten Wahrscheinlichkeit enthalten ist, muss alles bis zur 5 abgezogen werden
$=$	$P (k \leq 9) - P (k \leq 5)$
$=$	$F (25; 0,15; 9) - F (25; 0,15; 5)$
$\approx$	$0,15938$

Wahrscheinlichkeit von $E_{4}$

Wahrscheinlichkeit von $E_{5}$

Wahrscheinlichkeit von $E_{6}$

Wahrscheinlichkeit von E4

Wahrscheinlichkeit von E5

Wahrscheinlichkeit von E6

Wahrscheinlichkeit von $E_{4}$

Wahrscheinlichkeit von $E_{5}$

Wahrscheinlichkeit von $E_{6}$