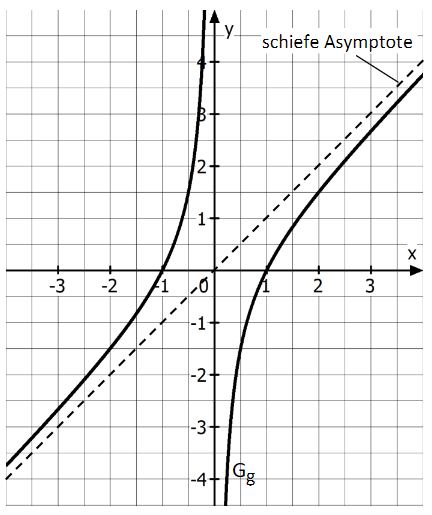
Lesen Sie die Nullstellen der Funktion $gg$ und die Gleichungen der Asymptoten des Graphen $G_{g}G\_g$ ab und geben Sie diese an.

Gegeben ist: $\mid {\int }_{-3}^{-2}g(x)\mathrm{d}x\mid \backslash left\; |\backslash int\_\{-3\}^\{-2\}\; g(x)\; \backslash mathrm\{d\}x\; \backslash right|$

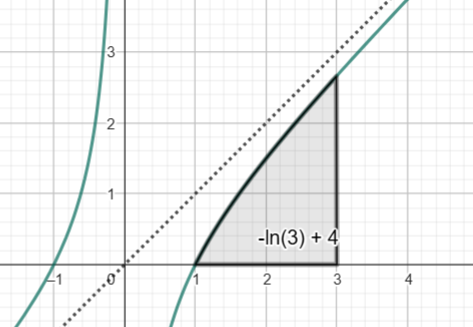
Dieser Wert kann geometrisch als Inhalt einer Fläche im Koordinatensystem der Aufgabenstellung interpretiert werden. Kennzeichnen Sie dieses zugehörige Flächenstück im Koordinatensystem oben.

Begründen Sie, dass der Graph $G_g^{\mathrm{\prime }}G\_g\text{'}$ der Ableitungsfunktion $g^{\mathrm{\prime }}g\text{'}$ die waagrechte Asymptote mit der Gleichung $y=1y\; =\; 1$ besitzt. Zeichnen Sie sämtliche Asymptoten von $G_g^{\mathrm{\prime }}G\_g\text{'}$ in das Koordinatensystem der Aufgabenstellung ein und skizzieren Sie $G_g^{\mathrm{\prime }}G\_g\text{'}$ in dieses Koordinatensystem.

$GG$ ist eine Stammfunktion von $gg$ mit $D_G=\mathbb{R}D\_G=\backslash mathbb\{R\}$\{ 0 }. Der Graph der Stammfunktion $GG$ wird mit $G_{G}G\_G$ bezeichnet. Kreuzen Sie für jede der folgenden Aussagen jeweils an, ob Sie wahr oder falsch ist.

Hinweis: Setzen Sie Ihr Kreuz nur bei denjenigen Aussagen, bei denen Sie sicher sind. Jedes falsch gesetzte Kreuz geht mit -0,5 BE und jedes richtig gesetzte Kreuz mit +1 BE ein. Im ungünstigsten Fall wird die Aufgabe mit 0 BE gewertet.