Teil 1 Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier

Die Aufgaben in diesem Ordner sollen ohne Hilfsmittel wie Taschenrechner oder Formelsammlung bearbeitet werden.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Abbildung zeigt den Graphen $G_g$ einer gebrochenrationalen Funktion $g$ mit ihrer maximalen Definitionsmenge $D_g=\mathbb{R}$ \{ $0$ }. Der Graph $G_g$ ist punktsymmetrisch zum Koordinatenursprung, besitzt keine lokalen Extrempunkt und hat genau eine schiefe und genau eine senkrechte Asymptote.
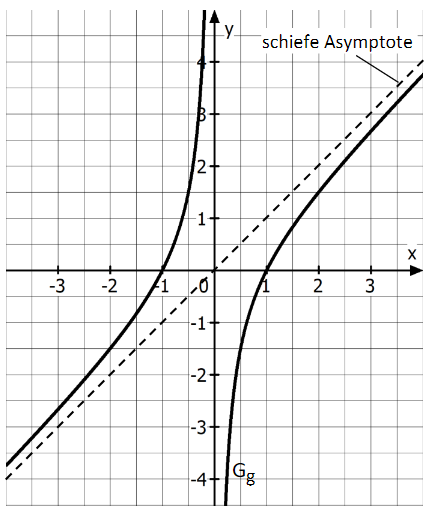
1. Lesen Sie die Nullstellen der Funktion $g$ und die Gleichungen der Asymptoten des Graphen $G_g$ ab und geben Sie diese an.
2. Gegeben ist: $\left |\int_{-3}^{-2} g(x) \mathrm{d}x \right|$
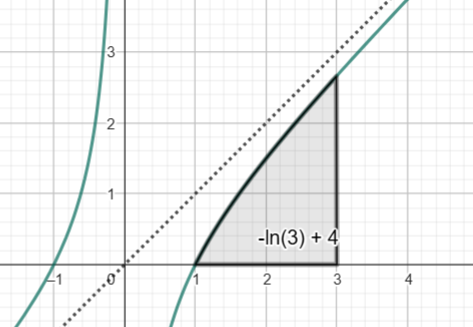
  Dieser Wert kann geometrisch als Inhalt einer Fläche im Koordinatensystem der Aufgabenstellung interpretiert werden. Kennzeichnen Sie dieses zugehörige Flächenstück im Koordinatensystem oben.
3. Begründen Sie, dass der Graph $G_g'$ der Ableitungsfunktion $g'$ die waagrechte Asymptote mit der Gleichung $y = 1$ besitzt. Zeichnen Sie sämtliche Asymptoten von $G_g'$ in das Koordinatensystem der Aufgabenstellung ein und skizzieren Sie $G_g'$ in dieses Koordinatensystem.
4. $G$ ist eine Stammfunktion von $g$ mit $D_G=\mathbb{R}$ \{ 0 }. Der Graph der Stammfunktion $G$ wird mit $G_G$ bezeichnet. Kreuzen Sie für jede der folgenden Aussagen jeweils an, ob Sie wahr oder falsch ist.
  Hinweis: Setzen Sie Ihr Kreuz nur bei denjenigen Aussagen, bei denen Sie sicher sind. Jedes falsch gesetzte Kreuz geht mit -0,5 BE und jedes richtig gesetzte Kreuz mit +1 BE ein. Im ungünstigsten Fall wird die Aufgabe mit 0 BE gewertet.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Abbildung zeigt modellhaft den Querschnitt eines Staudammes, der 100 Meter lang ist. Die Querschnittsfläche des Staudamms hat über die gesamte Länge hinweg die gleiche Form. Die krummlinige Begrenzungslinie der Querschnittsfläche kann durch den Graphen der Funktion $h$ mit $h(x)=(2-x)\cdot e^x$ und $D_h=[ -4;2 ]$ in einem kartesischen Koordinatensystem dargestellt werden. Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität. Bei den Rechnungen kann auf die Mitführung der Einheiten verzichtet werden.
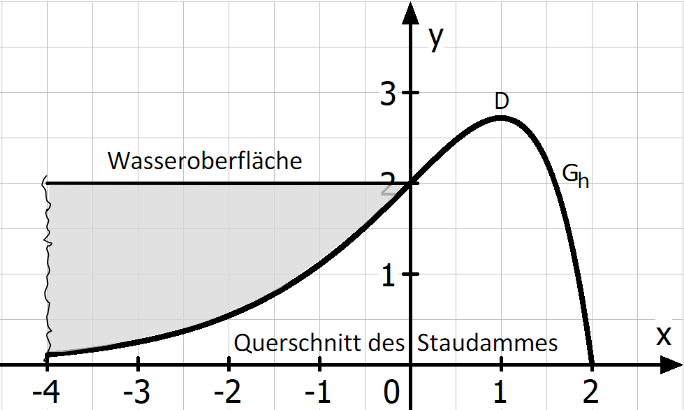
1. Der Punkt $D$ ist der höchste Punkt des Staudammes. Berechnen Sie die Koordinaten des Punktes $D$ . Weisen Sie auch nach, dass ein relativer Hochpunkt vorliegt.
2. Ein Kubikmeter des zur Aufschüttung des Staudamms verwendeten Materials hat die Masse $1{,}8$ Tonnen. Aufgrund der Verdichtung des Materials beim Bau des Staudamms ist das Volumen des tatsächlich benötigten Materials um $6$ % höher, als das theoretisch berechnete. Stellen Sie einen Ansatz auf, mit dem man die Masse des aufgeschütteten Materials in Tonnen berechnen kann.
  Hinweis: Die Berechnung soll nicht durchgeführt werden

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?