Die Abbildung zeigt modellhaft den Querschnitt eines Staudammes, der Meter lang ist. Die Querschnittsfläche des Staudamms hat über die gesamte Länge hinweg die gleiche Form. Die krummlinige Begrenzungslinie der Querschnittsfläche kann durch den Graphen der Funktion mit und in einem kartesischen Koordinatensystem dargestellt werden. Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität. Bei den Rechnungen kann auf die Mitführung der Einheiten verzichtet werden.
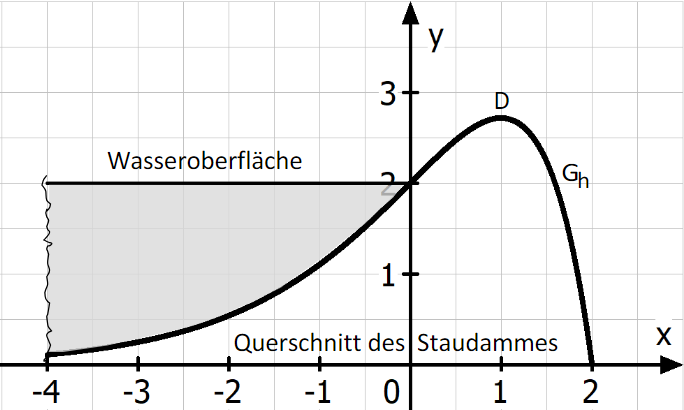
Der Punkt ist der höchste Punkt des Staudammes. Berechnen Sie die Koordinaten des Punktes . Weisen Sie auch nach, dass ein relativer Hochpunkt vorliegt. (5 BE)
Ein Kubikmeter des zur Aufschüttung des Staudamms verwendeten Materials hat die Masse Tonnen. Aufgrund der Verdichtung des Materials beim Bau des Staudamms ist das Volumen des tatsächlich benötigten Materials um höher, als das theoretisch berechnete. Stellen Sie einen Ansatz auf, mit dem man die Masse des aufgeschütteten Materials in Tonnen berechnen kann. (4 BE)
Hinweis: Die Berechnung soll nicht durchgeführt werden
