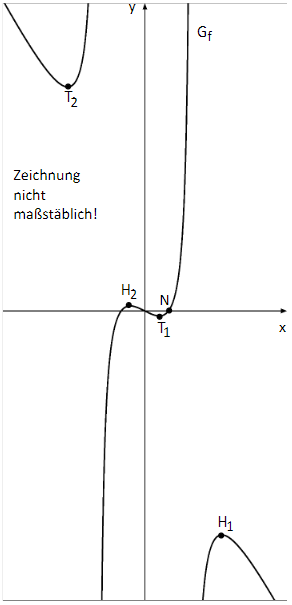
Bestimmen Sie $D_{f}D\_f$ sowie die Nullstellen von $ff$ und geben Sie jeweils die Art der Definitionslücken von $ff$ an.

$G_{f}G\_f$ besitzt genau vier lokale Extrempunkte. Die Koordinaten der beiden Extrempunkte $H_{1}H\_1$ und $T_{1}T\_1$ ergeben sich auf zwei Nachkommastellen gerundet zu $H_1(\mathrm{3,26}\mathrm{\mid }-\mathrm{4,74})H\_1\; (3\{,\}26|\; -\; 4\{,\}74)$ bzw. $T_1(\mathrm{0,61}\mathrm{\mid }-\mathrm{0,11})T\_1\; (0\{,\}61|\; -\; 0\{,\}11)$. Zeigen Sie rechnerisch, dass $G_{f}G\_f$ punktsymmetrisch zum Ursprung ist und geben Sie anschließend die gerundeten Koordinaten der Extrempunkte $H_{2}H\_2$ und $T_{2}T\_2$ an.

Ermitteln Sie für jede Asymptote von $G_{f}G\_f$ ihre Art und ihre Gleichung.

$G_{f}G\_f$ schneidet die x-Achse für $x>0x\; >\; 0$ im Punkt $NN$ (siehe Abbildung). Ermitteln Sie die Gleichung der Tangente an $G_{f}G\_f$ im Punkt $NN$.

[Teilergebnis: $f^{\mathrm{\prime }}(x)={\displaystyle \frac{-4x^4+11x^2-4}{(4-x^2{)}^2}}f\text{'}(x)=\backslash dfrac\{-4x^4+11x^2-4\}\{(4-x^2)^2\}$ ]

Gegeben sind die Gleichungen der zweiten, dritten und vierten Ableitungsfunktion der Funktion $ff$:

$f^{\mathrm{\prime }\mathrm{\prime }}(x)={\displaystyle \frac{6(x^3+12x)}{(4-x^2{)}^3}}f\text{'}\text{'}(x)=\; \backslash dfrac\{6(x^3+12x)\}\{(4-x^2)^3\}$

$f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}(x)={\displaystyle \frac{18(x^4+24x^2+16)}{(4-x^2{)}^4}}f\text{'}\text{'}\text{'}(x)=\backslash dfrac\{18(x^4+24x^2+16)\}\{(4-x^2)^4\}$

$f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}(x)={\displaystyle \frac{72(x^5+40x^3+80x)}{(4-x^2{)}^5}}f\text{'}\text{'}\text{'}\text{'}(x)=\backslash dfrac\{72(x^5+40x^3+80x)\}\{(4-x^2)^5\}$

(Nachweis nicht erforderlich!)

Es gilt: $D_f^{\mathrm{\prime }\mathrm{\prime }}=D_f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}=D_f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}D\_f\text{'}\text{'}=D\_f\text{'}\text{'}\text{'}=D\_f\text{'}\text{'}\text{'}\text{'}$

Untersuchen Sie die vierte Ableitungsfunktion $f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}f\text{'}\text{'}\text{'}\text{'}$ auf Nullstellen. Tragen Sie ausgehend von den gegebenen Ableitungen die fehlenden Zahlen in die leeren Kästchen im Term der fünften Ableitungsfunktion $f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}f\text{'}\text{'}\text{'}\text{'}\text{'}$ ein.

$f^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}(x)={\displaystyle \frac{\mathrm{\square }\cdot (x^{\mathrm{\square }}+60x^{\mathrm{\square }}+240x^{\mathrm{\square }}+64}{(4-x^2{)}^{\mathrm{\square }}}}f\text{'}\text{'}\text{'}\text{'}\text{'}(x)=\backslash dfrac\{\backslash square\; \backslash cdot\; (x^\{\backslash square\}+60x^\{\backslash square\}+240x^\{\backslash square\}+64\}\{(4-x^2)^\{\backslash square\}\}$