Teil 2 Analysis 2 - lernen mit Serlo!

Eine Kette ist an ihren Enden an zwei Punkten aufgehängt. Die beiden Aufhängepunkte haben einen waagrechten Abstand von $10 c m$ und sind auf gleicher Höhe angebracht. Der Verlauf der Kette wird modellhaft in einem kartesischen Koordinatensystem durch den Graphen $G_{K}$ (siehe Abbildung) der Funktion $K$ beschrieben. Die Funktion $K$ ist dabei gegeben durch die Gleichung $K (x) = 2 \cdot (e^{0,25 x - 1,25} + e^{- 0,25 x + 1,25})$ mit $D_{K} =$ $[0; 10]$ . Die Koordinaten der Punkte sind Längenangaben in der Einheit Zentimeter. Auf die Mitführung der Einheiten kann verzichtet werden.

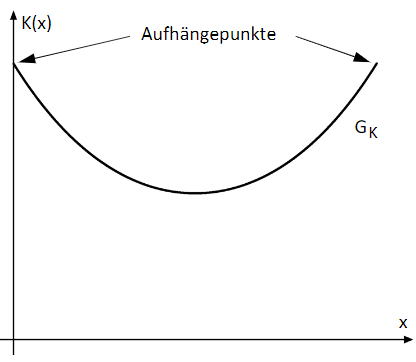
Ermitteln Sie die Koordinaten des tiefsten Punktes der Kette und führen Sie den rechnerischen Nachweis, dass es sich dabei um einen lokalen Tiefpunkt handelt.
[ Mögliches Teilergebnis: $K^{'} (x) = 0,5 (e^{0,25 x - 1,25} - e^{- 0,25 x + 1,25})$ ]
Der Kettenverlauf kann durch eine Parabel $G_{p}$ angenähert werden, die durch den Punkt $Q (0 | 7,554)$ und ihren Scheitelpunkt $S (5 | 4)$ verläuft. Ermitteln Sie die Gleichung der zugehörigen quadratischen Funktion $p$ .
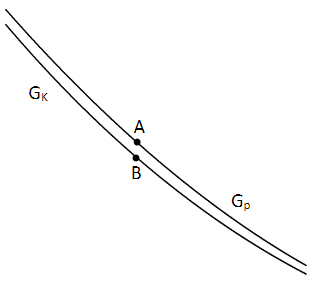
Die Parabel $G_{p}$ verläuft für $x \in] 0; 5 [$ stets oberhalb des Graphen $G_{K}$ . In diesem Bereich wird der Abstand der senkrecht übereinander liegenden Punkte $A (x | p (x)) \in G_{p}$ und $B (x | K (x)) \in G_{K}$ betrachtet. Die Abbildung zeigt einen nicht maßstabsgerechten, vergrößerten Ausschnitt von $G_{p}$ und $G_{K}$ . Der größte dieser Abstände ist ein Maß dafür, wie gut die Parabel $G_{p}$ den Graphen $G_{K}$ im Bereich $0 < x < 5$ annähert. Beschreiben Sie, wie dieser größte Abstand rechnerisch bestimmt werden kann.
Hinweis: Eine rechnerische Lösung soll nicht durchgeführt werden.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?