Aus statistischen Daten ergeben sich die Werte $S(0)=\mathrm{3,80}S(0)\; =\; 3\{,\}80$ und $S(12)=\mathrm{2,45}S(12)\; =\; 2\{,\}45$. Bestimmen Sie mithilfe der beiden Angaben die Werte der Parameter $aa$ und $bb$.

[ Mögliche Ergebnisse: $a\approx \mathrm{2,13}a\backslash approx\; 2\{,\}13$; $b\approx \mathrm{0,015}b\backslash approx0\{,\}015$ ]

Ermitteln Sie die Anzahl der pro Monat gesendeten SMS, die sich nach diesem Modell langfristig einstellen wird.

Zeigen Sie rechnerisch, dass nach diesem Modell die Anzahl der versendeten SMS pro Monat seit Januar 2013 stets gesunken ist.

Zeichnen Sie den Graphen der Funktion $SS$ für $0\le t\le 1000\backslash le\; t\; \backslash le\; 100$ in ein kartesisches Koordinatensystem. Wählen Sie auf beiden Achsen einen geeigneten Maßstab.

Es gilt für den Wert des bestimmten Integrals: ${\int }_0^{84}S(t)\mathrm{d}t\approx \mathrm{116,98}\backslash int\_\{0\}^\{84\}\; S(t)\; \backslash mathrm\{d\}t\backslash approx\; 116\{,\}98$

(Nachweis nicht erforderlich!).

Die folgende Tabelle gibt die gesamte Anzahl der in Deutschland in den einzelnen Kalenderjahren 2013 bis 2019 verschickten SMS in Milliarden an

(Quelle: Bundesnetzagentur).

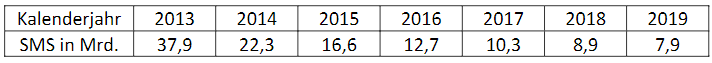
Interpretieren Sie den Wert des angegebenen Integrals und überprüfen Sie die Realitätsnähe des Modells mithilfe der von der Bundesnetzagentur veröffentlichten Zahlen.