Aufgabe 3: Zahlenpaare
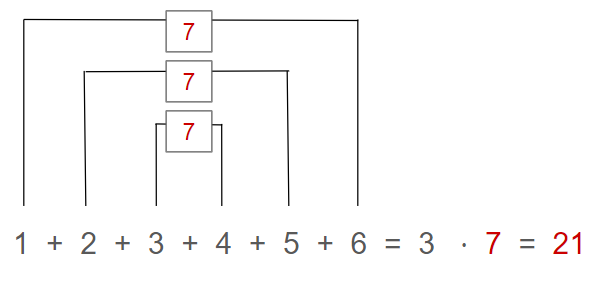
Merle hat Spaß an Zahlen und ist immer auf der Suche nach Tricks, um den Rechenaufwand einer Aufgabe zu verringern. Bei der Addition der Zahlen von 1 bis 10 bemerkt sie:
„Die beiden Zahlen 1 und 10 ergeben zusammen 11, ebenso wie die beiden Zahlen 2 und 9, die Zahlen 3 und 8 usw. Da ich so fünf Zahlenpaare jeweils mit dem Wert 11 bilden kann, muss ich nur rechnen und erhalte das Ergebnis 55.“ (Abbildung 1)
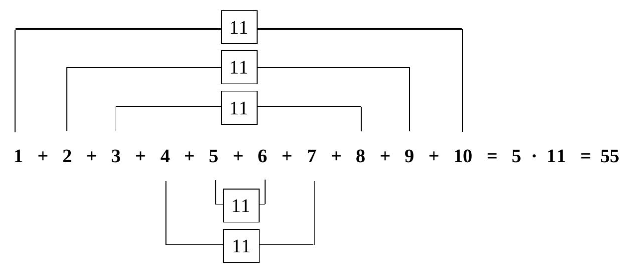
Abbildung 1: Rechentrick für die Addition der Zahlen von 1 bis 10
Wende Merles Trick auf die Addition der Zahlen von 1 bis 6 an, indem du Abbildung 2 vervollständigst. (2 P)
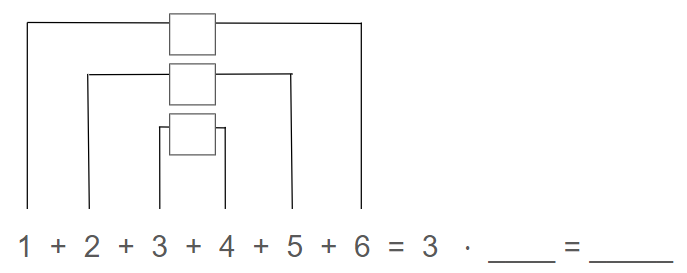
Abbildung 2: Addition der Zahlen von 1 bis 6
Merle verwendet den Trick für aufwendigere Additionen. Damit die Rechnungen übersichtlich bleiben, ersetzt sie fehlende Summanden durch Pünktchen. In Abbildung 3 ist Merles Berechnung für die Summe der Zahlen von 1 bis 30 dargestellt.
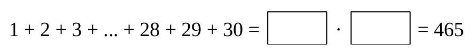
Abbildung 3: Addition der Zahlen von 1 bis 30
Begründe, dass in den Kästchen die Zahlen 15 bzw. 31 stehen müssen. (2 P)
Merle findet einen allgemeinen Term, um die Summe der Zahlen von 1 bis zu berechnen.
Sie notiert .
(1) Berechne mit dem Term den Wert der Summe für . (2 P)
(2) Erläutere die Bedeutung der Faktoren und im Zusammenhang mit dem Rechentrick. (2 P)
Merle formt den Term um und erhält .
Berechne den Wert der Summe für mit diesem vereinfachten Term. (2 P)
(1) Berechne die beiden Lösungen der Gleichung . (4 P)
(2) Erkläre, warum nur eine Lösung für den Kontext sinnvoll ist. (2 P)
„Bei meinem Rechentrick muss man die Summanden paarweise zusammenfassen. Daher nehme ich an, dass meine Formel für ungerade Zahlen nicht gilt“, meint Merle.
Für ungerade Zahlen n entwickeln Merle und ihr Freund Silas den Term .
Silas behauptet: „Es ist egal, welchen Term wir nehmen, da die Terme und gleichwertig sind."
Zeige durch Termumformungen, dass Silas Behauptung stimmt. (3 P)