Aufgabe 2A
Ein Großhändler bietet Rohkaffee in Säcken zu jeweils an. aller Säcke entsprechen den Qualitätsanforderungen. Die Zufallsgröße beschreibt die Anzahl der Säcke, die den Qualitätsanforderungen entsprechen. Sie ist binomialverteilt.
Der Großhändler liefert Säcke aus.
Bestimmen Sie die zu erwartende Anzahl der Säcke, die den Qualitätsanforderungen entsprechen.
Ermitteln Sie ein -Prognoseintervall für die Anzahl der Säcke, die den Qualitätsanforderungen entsprechen. (5 BE)
Mit dem Term lässt sich die Wahrscheinlichkeit eines
Ereignisses im Sachzusammenhang berechnen.
Geben Sie das Ereignis an. (2 BE)
Ein Kunde prüft die Qualität des Kaffees, bevor er mit dem Großhändler einen Vertrag abschließt. Er untersucht zufällig ausgewählte Säcke daraufhin, ob sie den Qualitätsanforderungen entsprechen.
Wenn dies bei höchstens zwei Säcken nicht der Fall ist, dann wird der Vertrag abgeschlossen.
Wenn genau drei Säcke nicht den Qualitätsanforderungen entsprechen, dann werden in einem zweiten Schritt weitere zufällig ausgewählte Säcke daraufhin untersucht, ob sie den Qualitätsanforderungen entsprechen. Wenn von diesen Säcken höchstens ein Sack nicht den Qualitätsanforderungen entspricht, dann wird der Vertrag abgeschlossen.
Andernfalls kommt der Vertrag nicht zustande.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass der Vertrag abgeschlossen wird. (5 BE)
Weiterhin entsprechen aller Säcke den Qualitätsanforderungen. Jeder Sack, der den
Qualitätsanforderungen nicht entspricht, weist mindestens einen der beiden folgenden Mängel auf:
: „Der Kaffee weist zu viele Verunreinigungen auf.“
: „Der Sack enthält weniger als kg Kaffee.“
Ein Sack wird zufällig ausgewählt. Die Wahrscheinlichkeit dafür, dass dieser Sack den Mangel aufweist, beträgt .
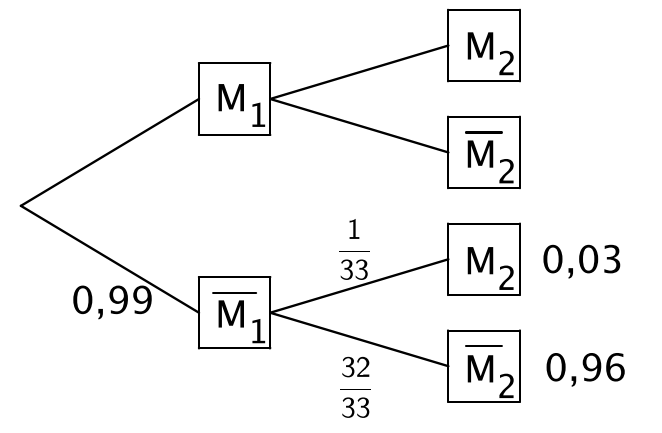
Ergänzen Sie die Wahrscheinlichkeiten in den Feldern in der unteren Hälfte des Baumdiagramms. (4 BE)
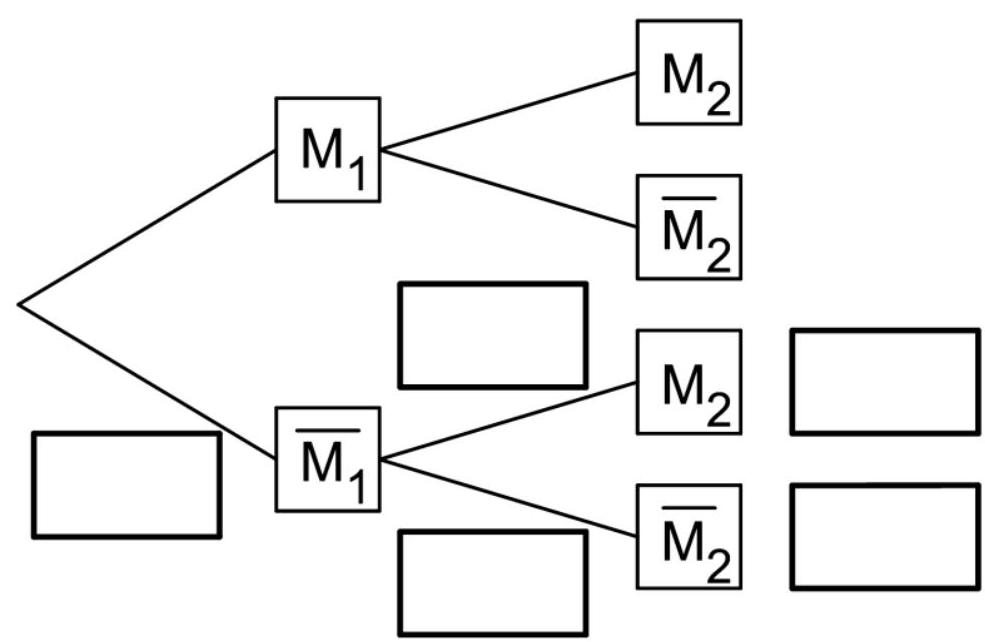
Das Auftreten der beiden Mängel ist stochastisch unabhängig.
Erläutern Sie im Sachkontext die Auswirkungen dieser Eigenschaft auf die Wahrscheinlichkeiten in der oberen Hälfte des Baumdiagramms. (4 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?