Aufgabe 2B
Die Abbildung zeigt das Netz eines Würfels.
Der Würfel wird -mal geworfen.
Die Zufallsgröße gibt an, wie oft die Zahl erzielt wird.
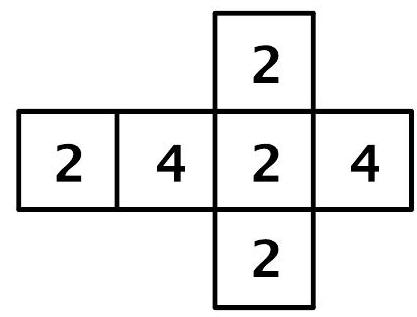
Abbildung 1
Begründen Sie, dass binomialverteilt mit dem Parameter ist. (3BE)
Ermitteln Sie die Wahrscheinlichkeit dafür, dass die Zahl häufiger erzielt wird als die Zahl „“. (2BE)
%Bestimmen Sie das kleinstmögliche zum Erwartungswert symmetrische Intervall, in dem die Anzahl der Würfe, in denen eine „4“ erzielt wird, mit einer Wahrscheinlichkeit von mindestens 80 % liegt. (3 BE)
Geben Sie im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term berechnet werden kann. (2BE)
Bei einem Spiel mit diesem Würfel werfen zwei Personen abwechselnd. Das Spiel ist beendet, wenn eine Person eine andere Zahl würfelt als die andere Person direkt vorher.
Es gewinnt die Person, die in ihrem letzten Wurf die größere Zahl hat.
Eine der beiden Personen beginnt das Spiel.
Berechnen Sie die Wahrscheinlichkeit dafür, dass diese Person verliert und der Würfel insgesamt höchstens viermal geworfen wird. (5BE)
Die Abbildung zeigt das Netz eines weiteren Würfels.
Der Würfel wird -mal geworfen.
Bei den ersten Würfen wird -mal die Zahl erzielt.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass bei höchstens der insgesamt Würfe die Zahl erzielt wird. (4BE)
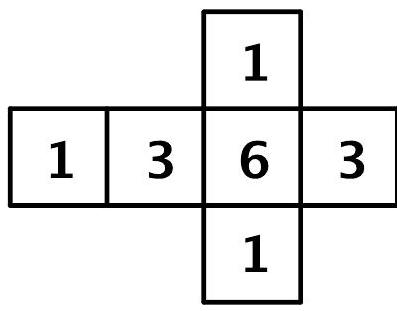
Abbildung 2
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?