1 Warum dieser Kurs?
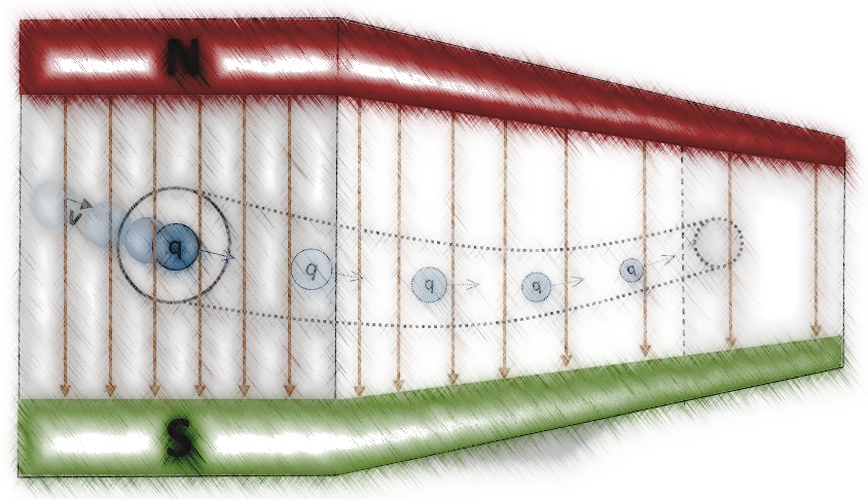
Abb. 1: Ablenkung einer frei beweglichen Ladung q im Magnetfeld
Wir haben bereits bei der Darstellung des Phänomens Magnetismus (siehe Link) und
der Definition der Magnetischen Flußdichte mit der Kraftwirkung auf einen stromdurchflossenen Leiter im Magnetfeld hingewiesen.
In nachfolgendem Kurs soll zunächst aufgezeigt werden, inwieweit dies ebenso auf frei bewegliche einzelne Ladungen (siehe skizzenhafte Darstellung Abb. 1) ausserhalb eines elektrischen Leiters gilt.
Um die Tragweite dieser entstehenden Kräfte, der sogenannten Lorentz-Kraft vollständig darzustellen, fassen wir alle gesammelten Erkenntnisse zusammen und verweisen auf den technisch wie praktischen Nutzen in unserem Alltag
2 Ladung Q und Strom I
1) Die Ladung
Mit Herleitung und Definition des Coulombschen Gesetzes (siehe LINK) haben wir uns bereits mit dem Ladungsbegriff auseinandergesetzt.
Die kleinste vorkommende Ladung genannt auch Elementarladung (Elektron , Proton ), beträgt exakt (für Coulomb). Dieser Wert ist negativ bei Elektronen, positiv bei Protonen
Die Einheit C wurde benannt nach Charles Augustin des Coulomb (siehe WIKIPEDIA).
Für den Ausdruck von Ladungen oftmals verwendet werden die Variablen oder .
Wir einigen uns an dieser Stelle an eine übliche Verwendung insofern . . .
eine einzelne Ladung mit (Elementarladung) bezeichnet wird, ob nun positiv oder negativ.
als Unterscheidung eine Vielzahl dieser "Einzel"- oder Elementarladungen mit beschrieben werden. Alles klar?
2) Elektrischer Strom
Ein "Strom" (hier ) ist ein Fluß von etwas. Der Elektrische Strom ist dementsprechend definiert, welche Ladungsmenge innerhalb einer bestimmten Zeit fließt.
Als Formel ausgedrückt:
Einheit:
3 Kräfte im Magnetfeld
1) Kraft auf einen stromdurchflossenen Leiter
Wir drücken die Magnetische Flußdichte aus mit:
Die Kraftwirkung des Magnetischen Feldes umgestellt somit:
2) Kraft auf eine bewegte Ladung q
In der Formel zu Ermittlung der der Kraft aus eben,
ersetzen wir In nächsten Schritten nun und :
Den Strom und
Die Geschwindigkeit: Weg pro Zeit ; Somit der Weg
. . . eingesetzt, erhalten wir:
Wir erhalten somit eine Beziehung,
einer wirkenden Kraft
auf eine mit der Geschwindigkeit bewegte Ladung
in einem Magnetfeld der Magnetischen Flußdichte beschreibt,
welche als sogenante Lorenz-Kraft definiert wurde.
4 Ermittlung von Kraftrichtungen
Bewegt sich eine Elementarladung (Elektron) oder (Proton) mit der Geschwindigkeit in ein vorherrschendes Magnetisches Feld der Flußdichte ( ⊥ ) wird durch die auftretende Lorentz-Kraft . . .
. . . das sich bewegende Elektron nach unten sowie
. . . das sich bewegende Proton nach oben abgelenkt
Dieses Phänomen ist in nachfolgender Abb. 2 exemplarisch dargestellt:
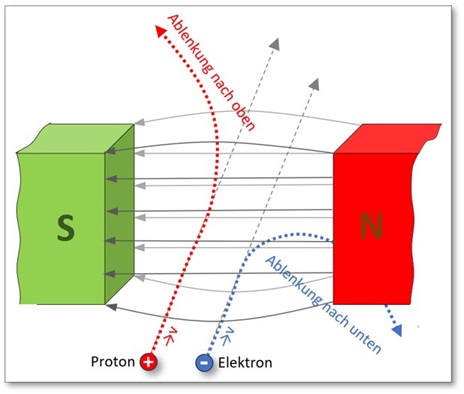
Abb. 2: Ablenkung von Elemtarladungen im Magnetfeld
Ermittlung der Richtung der Lorentz-Kraft
Um die jeweilige Richtung der Lorentz-Kraft einfach zu ermitteln, verwenden wir unsere rechte oder linke Hand. Betrachten wir sich bewegende Elektronen () so benutzen wir unsere linke Hand, im anderen Fall für Protonen () unsere rechte Hand. Beispielhaft hierzu die nachfolgende Abb. 3:
Die jeweils ausgestreckten Finger geben die Bewegungsrichtung mit der Geschwindigkeit an
Die gebeugten Finger die Ausrichtung des -Feldes (in unserem Falle von "Nord nach Süd", also von rechts nach links)
Der ausgestreckte Daumen die sich ergebenden Kraftrichtung , in einem Fall für Elektronen , andererseit für Protonen
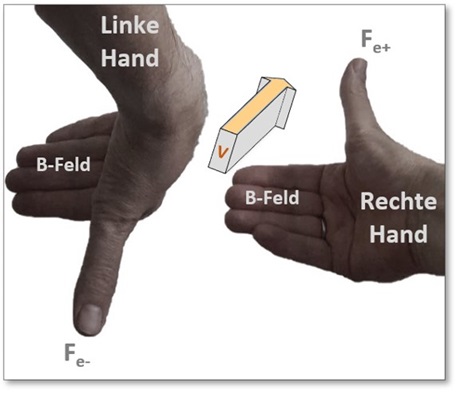
Abb. 3: Hilfsmittel zur Ermittlung einer Kraftrichtung
5 Kreis- und Spiralförmige Bewegungen im Magnetfeld
Kreisförmige Bewegungen im Magnetfeld
Wir können aus den bislang dargestellten Bahnbewegungen von Elektronen oder Protonen im Magnetfeld eine kreisförmige Ablenkung aufgrund der Lorentz-Kraft erkennen.
Interessant deshalb für uns an dieser Stelle, wie sich eine Elementarladung generell innerhalb eines ausgedehnten Magnetfeldes der Magnetischen Flußdichte (Vektorschreibweise!) bewegt. Können wir möglicherweise generell eine kreisförmige Bewegung ableiten?
In diesem Kurs hatten wir bislang angenommen, die Geschwindigkeit verliefe immer senkrecht zur Magnetischen Flußdichte ( ⊥ ).
Nachfolgend werden wir neben dieser bisherigen Annahme (1) ebenso den Bahnverlauf von Elementarladungen betrachten, wenn dem nicht so ist (2).
1) Geschwindigkeit senkrecht zum Magnetfeld
Für unsere weiteren Untersuchungen gehen wir deshalb zunächst davon aus,
. . . dass sich eine Elementarladung , beispielweise ein Proton bereits innerhalb eines Magnetfeldes befindet,
. . . des weiteren die Bewegungsrichtung der Geschwindigkeit zunächst absolut senkrecht zu den magnetischen Feldlinien verläuft (siehe nachfolgende Abb. 4)
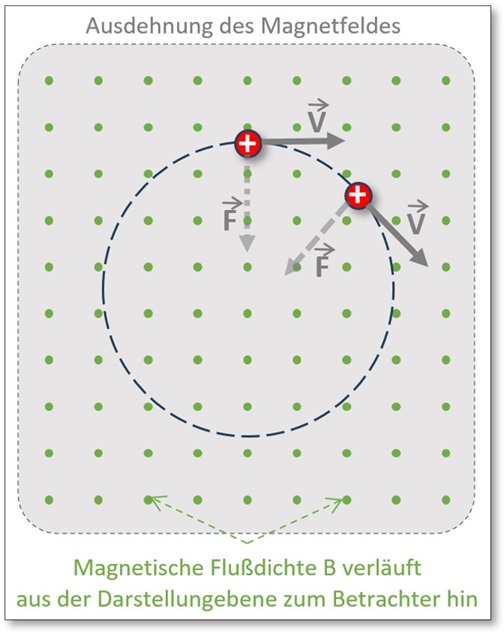
Abb. 4: Bahnbewegung Elementarladung q (Annahme: ⊥ )
2) Geschwindigkeit nicht senkrecht zum Magnetfeld (
Für unseren etwas geänderten Gedankengang nun folgendes,
. . . wiederum befindet sich eine hier positive Elementarladung (Proton) bereits innerhalb eines Magnetfeldes ,
. . . geändert nun allerdings die Bewegungsrichtung der Geschwindigkeit , nun nicht senkrecht zu den magnetischen Feldlinien (siehe nachfolgende Abb. 5).
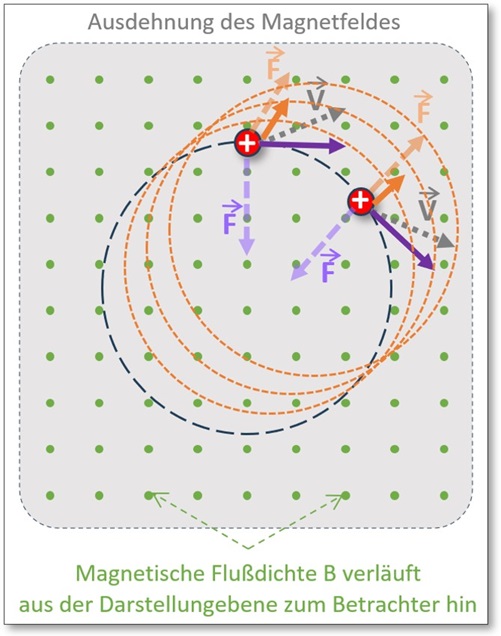
Abb. 5: Bahnbewegung Elementarladung (Annahme:
6 Leiter und Leiterschleifen
Bislang haben wir uns im vorliegenden Kurs mit der Kraftwirkung auf mit der Geschwindigkeit bewegte punktuelle elektrische Ladungen ( bzw. ) beschäftigt.
Um die spätere praktische Verwendbarkeit der Lorenz-Kraft vollständig erfassen zu können, widmen wir uns ergänzend den Kraftwirkungen auf Leiter und Leiterschleifen, also frei beweglichen Ladungen in elektrischen Leitern, in einem Magnetischen Feld der Flußdichte .
Bereits mit der Ableitung und Definition der Magnetischen Flußdichte haben wir die Kraftwirkung auf stromdurchflossene elektrische Leiter kennengelernt. (siehe LINK)
1) Die Kraftwirkung auf ein bewegliches Leiterstück
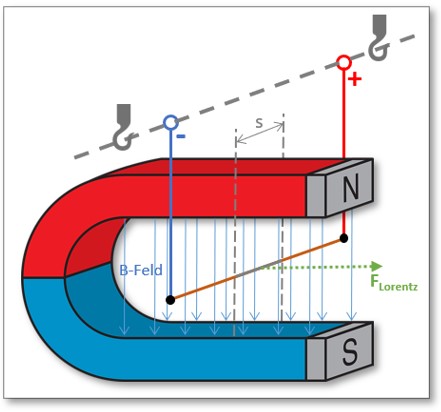
Abb. 6: Stromdurchflossenes bewegliches Leiterstück im Magnetfeld
Im Ergebnis erkennen wir je nach Anwendung der Rechte-Hand-Regel (für Protonen, technische Stromrichtung) oder Linke-Hand-Regel (für Elektronen, physikalische Stromrichtung) eine Bewegung nach rechts, also aus dem Magnetfeld heraus.
2) Die Kraftwirkung auf eine bewegliche Leiterschleife
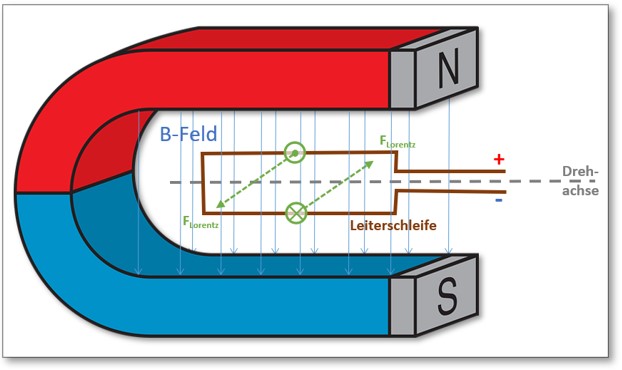
Abb. 7: Stromdurchflossene beweglich gelagerte Leiterschleife im Magnetfeld
Im Ergebnis erkennen wir je nach Anwendung der Rechte-Hand-Regel (für Protonen, technische Stromrichtung) oder Linke-Hand-Regel (für Elektronen, physikalische Stromrichtung) eine Drehbewegung, im gezeigten Beispiel gegen den Uhrzeigersinn (Linksdrehung)
7 Zusammenfassung
Grundsätzliches:
Alle bewegten Ladungen erfahren im Magnetfeld eine Kraftwirkung
Seien es mit Strom durchflossene Leiter (also darin sich bewegende Ladungen pro Zeit ) der Länge gemäß der Formel:
wirksame Leiterlänge: ⊥ -Feld
hier beispielsweise ohne Vektorschreibweise
. . . oder mit Geschwindigkeit bewegten Ladungen gemäß der Formel:
Geschwindigkeitsanteil ⊥ -Feld
hier beispielsweise in Vektorschreibweise
Die sich ergebenden Kraftrichtungen können wir . . .
mit der Rechte-Hand-Regel (für Protonen, technische Stromrichtung) oder
mit der Linke-Hand-Regel (für Elektronen, physikalische Stromrichtung) einfach ermitteln
Praktische Verwendung:
Anwendungen in der Ablenkung von Ladungen
Anwendungen in der Kraftwirkung auf Leiterstücke
Anwendungen in der Kraft- und Drehbewegung auf Leiterschleifen/Spulen
8 Aufgabe
Laden
Quellen:
https://pixabay.com
Bilder in Eigenkonstruktion
