Gegeben sind die Funktionen mit \ {0} und mit . Der Graph der Funktion heißt und der Graph der Funktion heißt . In der Abbildung ist ein Teil des Graphen für und der Graph dargestellt. ist die schräge Asymptote von .
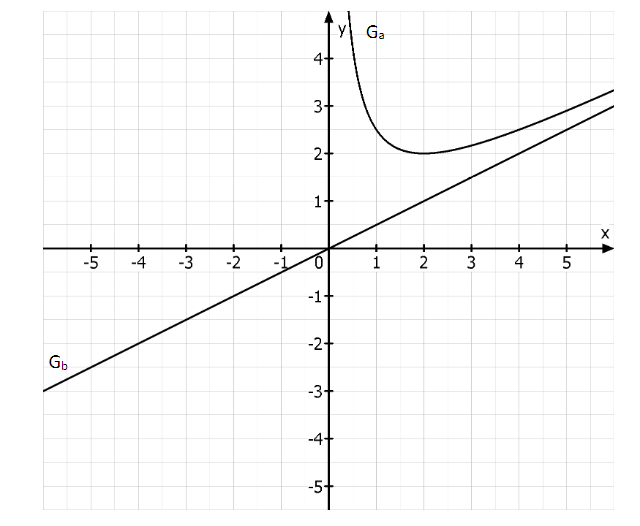
Zeigen Sie, dass der vollständige Graph punktsymmetrisch bezüglich des Koordinatenursprungs ist.
Geben Sie die Art und die ganzzahligen Koordinaten der relativen Extrempunkte von an und zeichnen Sie für in das Koordinatensystem von 1 ein.
Bestimmen Sie die Gleichung der Tangente an im Punkt .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
