Teil 1 Analysis
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Gegeben sind die Funktionen mit \ {0} und mit . Der Graph der Funktion heißt und der Graph der Funktion heißt . In der Abbildung ist ein Teil des Graphen für und der Graph dargestellt. ist die schräge Asymptote von .
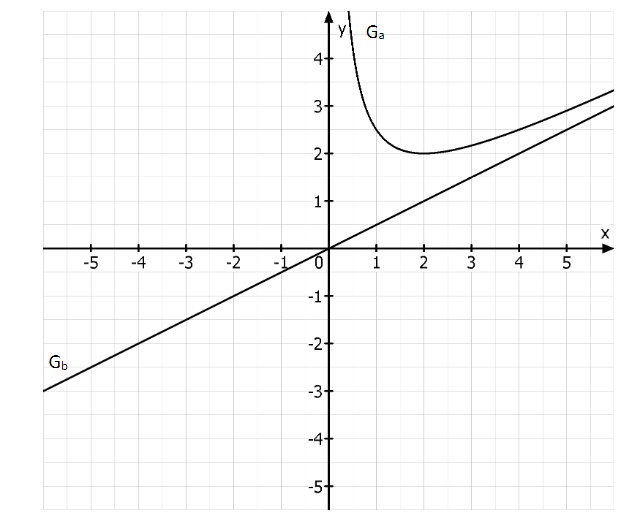
Zeigen Sie, dass der vollständige Graph punktsymmetrisch bezüglich des Koordinatenursprungs ist.
Geben Sie die Art und die ganzzahligen Koordinaten der relativen Extrempunkte von an und zeichnen Sie für in das Koordinatensystem von 1 ein.
Bestimmen Sie die Gleichung der Tangente an im Punkt .
- 2
Von einer gebrochenrationalen Funktion mit der Definitionsmenge \ {} und ihrem Graphen sind die folgenden Eigenschaften bekannt:
-Die Funktion hat eine Unendlichkeitsstelle mit Vorzeichenwechsel bei .
-Die Funktion hat eine stetig behebbare Definitionslücke bei .
-Die Funktion hat die einzige Nullstelle mit der Vielfachheit zwei.
-Es gilt: .
Bestimmen Sie eine Gleichung der Funktion so, dass die genannten Eigenschaften erfüllt sind.
- 3
Gegeben sind in ihren maximalen Definitionsmengen die reellen Funktionen
Die Abbildung zeigt die Graphen der Funktionen und .
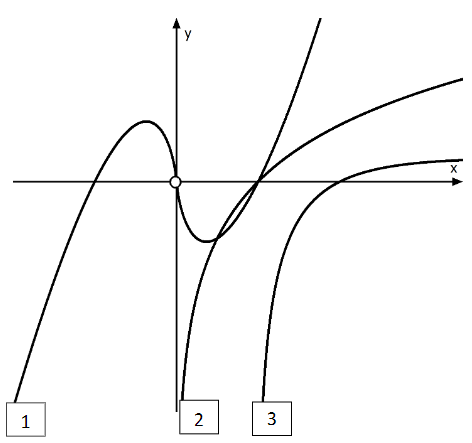
Ordnen Sie jeder Funktion den richtigen Graphen zu und geben Sie zu allen drei Funktionen jeweils die Definitionsmenge an.
Graph 1 und Graph 2 schließen im IV. Quadranten eine endliche Fläche ein. Beschreiben Sie ohne die Rechnungen durchzuführen, wie Sie die Maßzahl dieser Fläche ermitteln können.
- 4
Die Abbildung zeigt den Graphen der quadratischen Funktion mit dem Scheitel .
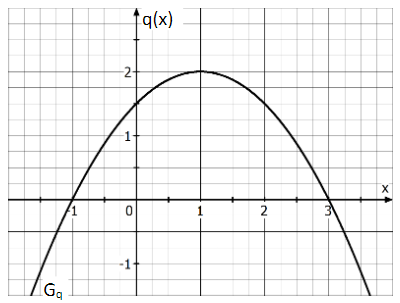
Für die Funktion gilt: . Für beide Funktionen gilt: .
Bestimmen Sie mithilfe der Abbildung die Wertemenge der Funktion . Begründen Sie dabei Ihre Vorgehensweise.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
