Ein Glücksrad ist in 20 gleich große Sektoren unterteilt, die entweder blau oder
gelb eingefärbt sind. Das Glücksrad wird 100-mal gedreht. Die binomialverteilte Zufallsgröße beschreibt, wie oft dabei die Farbe „Blau“, die binomialverteilte Zufallsgröße , wie oft dabei die Farbe „Gelb“ erzielt wird.
Begründen Sie, dass und die gleiche Standardabweichung haben.
Der Erwartungswert von ist ganzzahlig. Die Abbildung zeigt Werte der
Wahrscheinlichkeitsverteilung von .
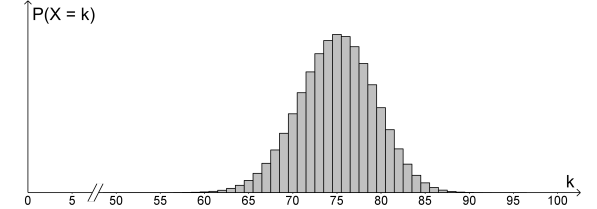
Bestimmen Sie die Anzahl der blauen Sektoren des Glücksrads.
