Untersuchen Sie, für welche Werte von $a$ die Vektoren $\overrightarrow{a}$ , $\overrightarrow{b}$ und $\overrightarrow{c}$ eine Basis des ${ℝ}^3$ bilden.

Für diese Teilaufgabe gilt $a=5$. Stellen Sie den Vektor $\overrightarrow{d}=\left(\begin{array}{c}-4\\ -2\\ -4\end{array}\right)$ als Linearkombination von $\overrightarrow{a}$ , $\overrightarrow{b}$ und $\overrightarrow{c}$ dar.

Der Punkt $P(2|0|0)$ und die Vektoren $\overrightarrow{a}$ und $\overrightarrow{b}$ legen die Ebene $F$ fest. Ermitteln Sie eine Gleichung für $F$ in Parameter- und Koordinatenform.

[ Mögliches Teilergebnis: $F:6x_1+4x_2+3x_3=12$ ]

Berechnen Sie die Schnittpunkte von $F$ mit den Koordinatenachsen und veranschaulichen Sie die Ebene $F$ in einem Koordinatensystem.

Gegeben ist die Geradenschar $g_a:\overrightarrow{x}=\left(\begin{array}{c}1\\ 2\\ 3\end{array}\right)+\mu \left(\begin{array}{c}1\\ a-1\\ 0\end{array}\right)$ mit $a,\mu \in ℝ$. Bestimmen Sie die gegenseitige Lage von $g_a$ und $F$ in Abhängigkeit von $a$. Bei der Bearbeitung können auch die Ergebnisse der Teilaufgabe 1.a) verwendet werden.

Gegeben sind die Punkte $A(2|\text{–}3|0),B(2|0|\text{–}4),D(\text{–}4|\text{–}2|\text{–}4)$ und $E(\text{–}4|\text{–}5|0)$ in einem kartesischen Koordinatensystem des ${ℝ}^3$.

1.) Zeigen Sie, dass das Viereck $DBAE$ ein Parallelogramm ist und begründen Sie, dass das Parallelogramm nicht in der Ebene $F$ aus Teilaufgabe 1.c) liegt.

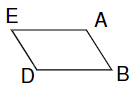
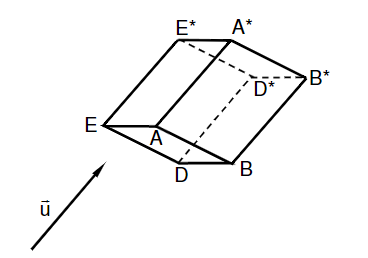
2.) Das Viereck $D$*$B$*$A$*$E$* geht durch Parallelverschiebung um den Vektor $\overrightarrow{u}=\left(\begin{array}{c}-\frac{4}{3}\\ 4\\ 3\end{array}\right)$ aus dem Viereck $DBAE$ hervor. Werden die Punkte $DBAE$ und die Punkte $D$*$B$*$A$*$E$* gemäß der Skizze verbunden, entsteht ein Prisma. Überprüfen Sie rechnerisch, ob sich die Diagonalen $DA$* und $BE$* des Prismas schneiden und geben Sie gegebenenfalls die Koordinaten des Schnittpunktes an.