Aufgabe Q2
Für eine Zahl zeigt die Abbildung den Graphen der in definierten Funktion mit sowie die Gerade . und schneiden sich im Koordinaten-ursprung und verläuft senkrecht zur Tangente an im Koordinatenursprung. Zudem berühren sich und die x-Achse im Punkt .
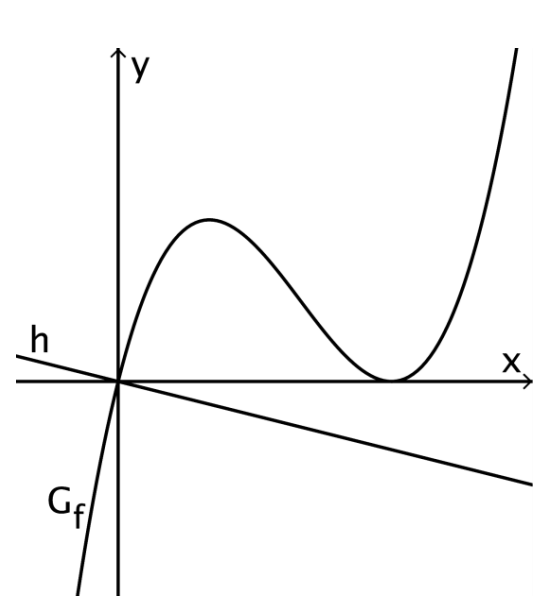
Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
Die beiden gemeinsamen Punkte von und der x-Achse sind zwei benachbarte Eckpunkte des Rechtecks.
Eine Diagonale liegt auf der Gerade .
Skizzieren Sie das Rechteck in der Abbildung und zeigen Sie, dass der Flächeninhalt des Rechtecks unabhängig von ist. [5 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
serlo.orgDieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
→ Was bedeutet das?
