Pflichtteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Wählen Sie von den Aufgaben Q1 bis Q6 genau zwei zur Bearbeitung aus.

1
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P1
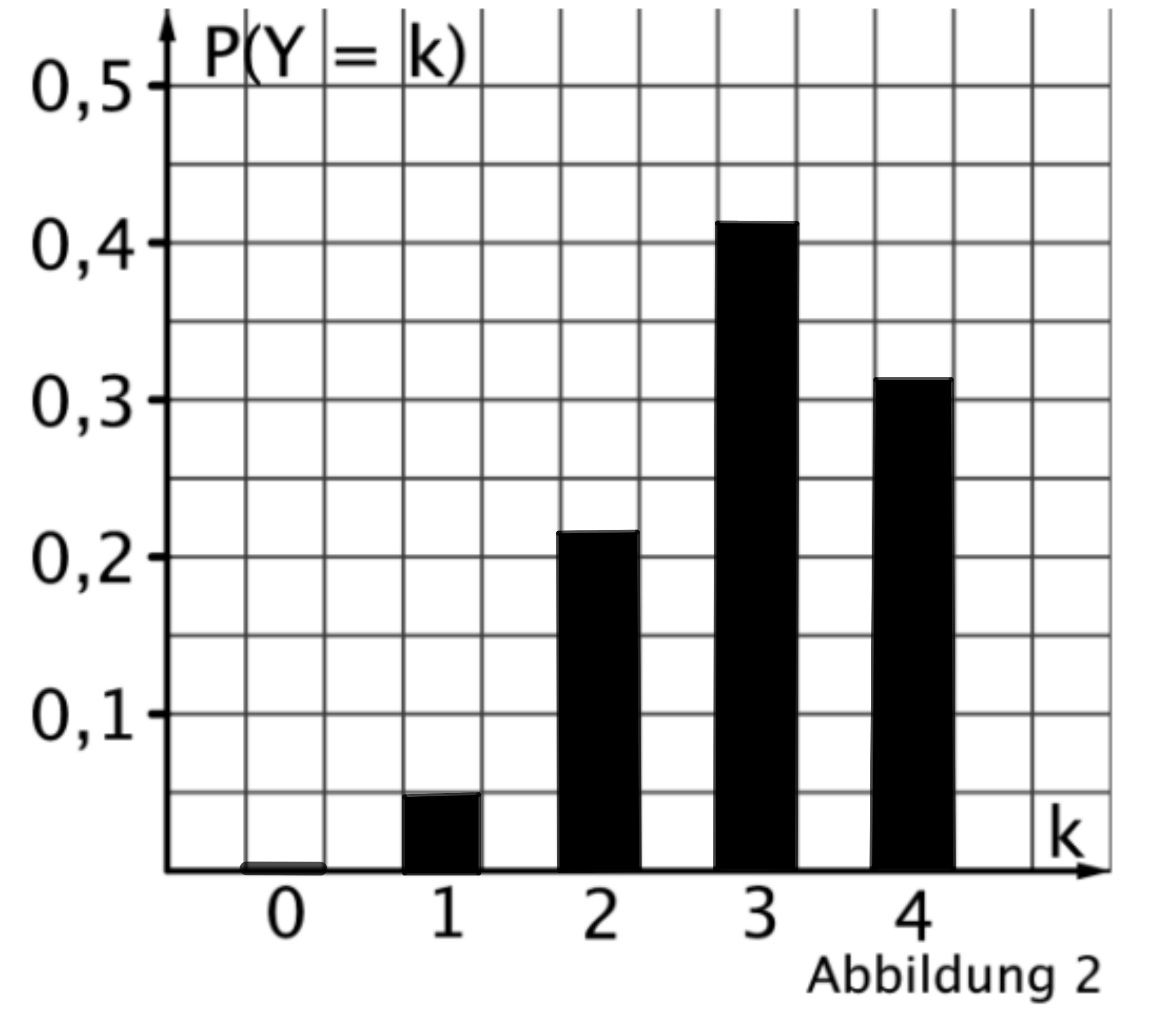
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = (1 - x^{2}) \cdot e^{- x}$
Eine Stammfunktion zu $f$ wird mit $F$
bezeichnet.
Abb. 1
1. Zeigen Sie rechnerisch, dass $f$ genau zwei Nullstellen besitzt. [2BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Setze $f (x) = 0$ :
  $0 = (1 - x^{2}) \cdot e^{- x}$
  Verwende den Satz vom Nullprodukt.
  Da $e^{- x} \neq 0$ für alle $x$ , kann nur $1 - x^{2} = 0$ sein:
  $\Rightarrow x_{1} = - 1$ und $x_{2} = 1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $f (x) = 0$ und verwende den Satz vom Nullprodukt.
2. Deuten Sie die Aussage $F (2, 5) - F (0) \approx 0$ in Bezug auf den Graphen von $f$ geometrisch. [3BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Es gilt: $F (2, 5) - F (0) = \int_{0}^{2,5} f (x) d x \approx 0$
  Betrachte in der Abbildung $1$ das Integrationsintervall:
  Im Intervallbereich $0$ bis $1$ verläuft der Funktionsgraph im positiven Bereich oberhalb der x-Achse (für $x = 1$ ist der Funktionswert gleich null) und man erhält einen positiven Flächeninhalt. Dieser Flächeninhalt ist etwa so groß wie der Inhalt der Fläche, die der Graph von $f$ unterhalb der x-Achse von $1$ bis $2,5$ mit dieser einschließt.
  Die Flächenbilanz ist demnach ungefähr gleich null.
  Die folgende Abbildung dient nur zur Veranschaulichung.
  Die Flächenbilanz ist ungefähr null.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte den Flächeninhalt im Intervallbereich $0$ bis $1$ und im Intervallbereich von $1$ bis $2,5$ .
  Wie groß ist die Flächenbilanz?
2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P2
Gegeben ist die Schar der in $ℝ$ definierten Funktionen $f_{a}$ mit $f_{a} (x) = a x^{3} + a x^{2}$ und $a \in ℝ^{+}$ .
1. Geben Sie den Wert von $a$ an, sodass der Punkt $(1 | 6)$ auf dem Graphen von $f_{a}$ liegt. [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
  Setze den Punkt $(1 | 6)$ in $f_{a} (x)$ ein:
  $6 = a \cdot 1^{3} + a \cdot 1^{2} = 2 \cdot a \Rightarrow a = 3$
  Für $a = 3$ liegt der Punkt $(1 | 6)$ auf $f_{3} (x)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze den Punkt $(1 | 6)$ in $f_{a} (x)$ ein.
2. Berechnen Sie in Abhängigkeit von $a$ den Inhalt der Fläche, die der Graph von $f_{a}$ mit der
  x-Achse einschließt. [4 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Für die Flächenberechnung werden die Nullstellen der Funktion benötigt:
  $f_{a} (x) = 0 \Rightarrow a x^{3} + a x^{2} = 0 \Rightarrow a x^{2} (x + 1) = 0$
  Wende den Satz vom Nullprodukt an:
  $x_{1,2} = 0$ und $x_{3} = - 1$
  Demnach muss für die Flächenberechnung das Integral von $- 1$ bis $0$ berechnet werden:
  $A (a) = \int_{- 1}^{0} a x^{3} + a x^{2} d x = {[\frac{a}{4} x^{4} + \frac{a}{3} x^{3}]}_{- 1}^{0} = 0 - (\frac{a}{4} \cdot (- 1)^{4} + \frac{a}{3} \cdot (- 1)^{3})$
  $A (a) = \frac{a}{3} - \frac{a}{4} = \frac{a}{12}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Nullstellen der Funktion $\Rightarrow$ $x_{1}$ und $x_{2}$
  Berechne dann $A (a) = \int_{x_{1}}^{x_{2}} f_{a} (x) d x$ .
3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P3
Ein Glücksrad ist in $20$ gleich große Sektoren unterteilt, die entweder blau oder gelb
eingefärbt sind. Das Glücksrad wird $100$ -mal gedreht.
Die binomialverteilte Zufallsgröße $X$ beschreibt, wie oft dabei die Farbe „Blau“, die
binomialverteilte Zufallsgröße $Y$ , wie oft dabei die Farbe „Gelb“ erzielt wird.
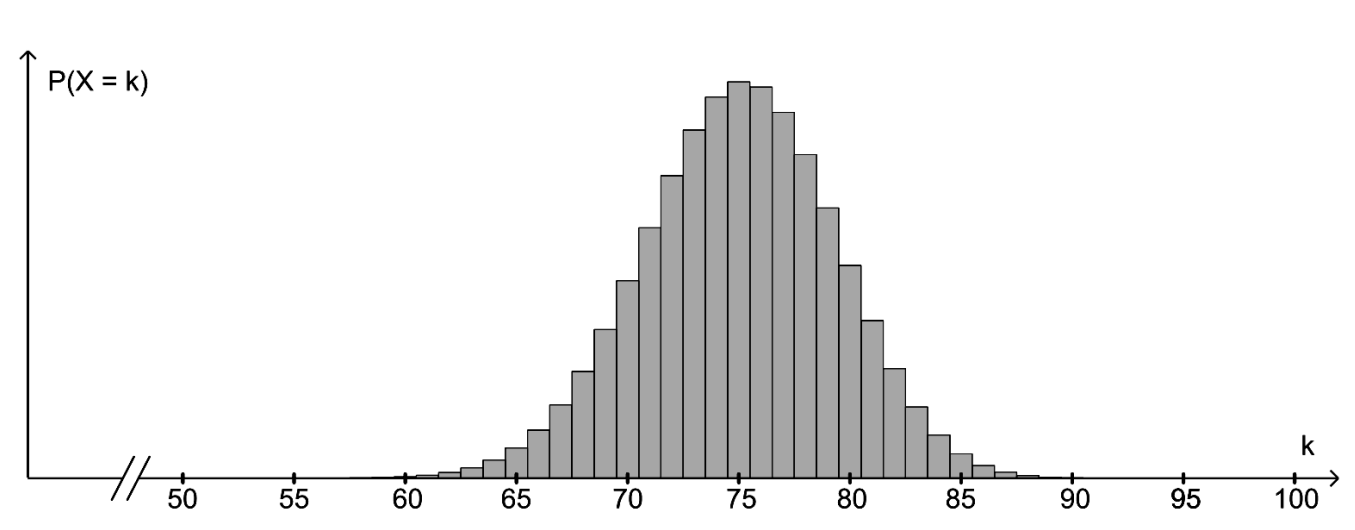
Abb. 2
1. Begründen Sie, dass $X$ und $Y$ die gleiche Standardabweichung haben. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Erwartungswert
  Die Wahrscheinlichkeit dafür, dass man ein blaues oder gelbes Feld trifft, ist nicht gegeben. Man bezeichnet also zunächst die Wahrscheinlichkeit dafür, dass man ein blaues Feld trifft, $p$ , und die Wahrscheinlichkeit dafür, dass man ein gelbes Feld trifft, $q$ .
  Wir wissen, dass $p + q = 1$ sein muss, da man nur entweder ein blaues oder ein gelbes Feld treffen kann.
  Der Erwartungswert beträgt, da es sich um eine Binomialverteilung handelt, für
  $X$ : $n \cdot p = 100 p$ und für $Y$ : $n \cdot q = 100 q$ .
  Varianz und Standardabweichung
  Die Varianz berechnet man bei einer Binomialverteilung mit der Formel
  $n \cdot p \cdot (1 - p) .$
  Varianz von $X : 100 \cdot p \cdot (1 - p) = 100 \cdot p \cdot q$
  Varianz von $Y : 100 \cdot q \cdot (1 - q) = 100 \cdot q \cdot p$
  ⇒ Varianz von $X$ = Varianz von $Y$
  Da die Standardabweichung die Quadratwurzel der Varianz ist, sind auch diese beiden Werte gleich.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Benenne die Trefferwahrscheinlichkeiten der beiden Ereignisse mit Variablen. Was verbindet die beiden Wahrscheinlichkeiten?
  Formuliere in Abhängigkeit von den Variablen Werte für die Varianz und die Standardabweichung und vergleiche sie.
2. Der Erwartungswert von $X$ ist ganzzahlig. Die Abbildung (Abb. 2) zeigt Werte der Wahrscheinlichkeitsverteilung von $X$ . Bestimmen Sie die Anzahl der blauen Sektoren des Glücksrads. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Der Wert, den die Zufallsvariable am wahrscheinlichsten annimmt, ist gleich der Erwartungswert. Diesen Wert kann man in der Abbildung ablesen, der höchste Balken ist bei der Zahl $75$ .
  $\Rightarrow E (X) = 75$
  Der Erwartungswert ist bei einer Binomialverteilung als Produkt aus $n$ und $p$ definiert.
  $\Rightarrow E (X) = n \cdot p = 100 \cdot p$
  Jetzt kann man die beiden Gleichungen gleichsetzen:
  $75$ $=$ $100 \cdot p$ $: 100$
  $\frac{75}{100}$ $=$ $p$
  ↓
  Kürze.
  $\frac{3}{4}$ $=$ $p$
  Die Zufallsvariable $X$ hat also eine Trefferwahrscheinlichkeit $p$ von $0,75$ . Da das Glücksrad insgesamt $20$ gleich große Felder hat, müssen $20 \cdot 0,75 = 15$ davon blau sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Wert, den die Zufallsvariable am wahrscheinlichsten annimmt, ist gleich der Erwartungswert E(X). Diesen Wert kann man in der Abbildung ablesen.
  Weiterhin gilt: $E (X) = n \cdot p = 100 \cdot p$
  Setze den abgelesenen Wert für $E$ in die Gleichung ein und löse nach $p$ auf.
  Die Anzahl der blauen Felder ist dann gleich $20$ mal $p$ .
4
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P4
Die Punkte $𝐵 (4 | 3 | 12)$ und $𝐶 (2 | 4 | 10)$ sind
Eckpunkte eines Parallelogramms $𝐴 𝐵 𝐶 𝐷$ , dessen Diagonalen sich im Punkt $𝑀 (3 | 2 | 1)$ schneiden.
1. Verschiebt man jeden der Punkte $𝐴, 𝐵, 𝐶, 𝐷$ und $𝑀$ parallel zur $𝑥_{3}$ -Achse in die
  $x_{1} x_{2}$ -Ebene, so ergeben sich die Punkte $A^{'}, B^{'}, C^{'}, D^{'}$ bzw. $M^{'}$ . Das Viereck $A^{'} B^{'} C^{'} D^{'}$ ist ein Parallelogramm, dessen Diagonalen sich im Punkt $M^{'}$ schneiden. Zeichnen Sie das Viereck $A^{'} B^{'} C^{'} D^{'}$ und $M^{'}$ in die Abbildung ein. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Das zweidimensionale kartesische Koordinatensystem
  Es gilt: $B^{'} (4 | 3), C^{'} (2 | 4)$ und $M^{'} (3 | 2)$ .
  Diese drei Punkte werden in das Koordinatensystem eingezeichnet und zu einem Parallelogramm ergänzt:
  Parallelogramm
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $B^{'} (4 | 3), C^{'} (2 | 4)$ und $M^{'} (3 | 2)$ .
  Diese drei Punkte werden in das Koordinatensystem eingezeichnet und zu einem Parallelogramm ergänzt.
2. Berechnen Sie den Wert des Skalarprodukts $\vec{C M} \circ \vec{C B} = (\begin{array}{c} 1 \\ - 2 \\ - 9 \end{array}) \circ (\begin{array}{c} 2 \\ - 1 \\ 2 \end{array})$ und beurteilen Sie, ob der Winkel zwischen den Vektoren $\vec{C M}$ und $\vec{C B}$ kleiner als $90^{\circ}$ ist.
  [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Berechne das Skalarprodukt:
  $(\begin{array}{c} 1 \\ - 2 \\ - 9 \end{array}) \circ (\begin{array}{c} 2 \\ - 1 \\ 2 \end{array}) = 1 \cdot 2 + (- 2) \cdot (- 1) + (- 9) \cdot 2 = 2 + 2 - 18 = - 14$
  Das Skalarprodukt ist negativ, d.h. der Winkel ist nicht kleiner als $90^{\circ}$ .
  (Der Winkel ist größer als $90^{\circ}$ .)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne das Skalarprodukt.
  Ist das Skalarprodukt negativ, dann ist der Winkel nicht kleiner als $90^{\circ}$ .
5
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q1
Gegeben ist für jede positive reelle Zahl 𝑎 die in $ℝ$ definierte Funktion $f_{a}$ mit $f_{a} (x) = a \cdot x^{2}$ .
Die Abbildung zeigt den Graphen von $f_{\frac{1}{2}}$ sowie die Tangente 𝑡 an den Graphen von $f_{\frac{1}{2}}$
im Punkt $(4 | f_{\frac{1}{2}} (4))$
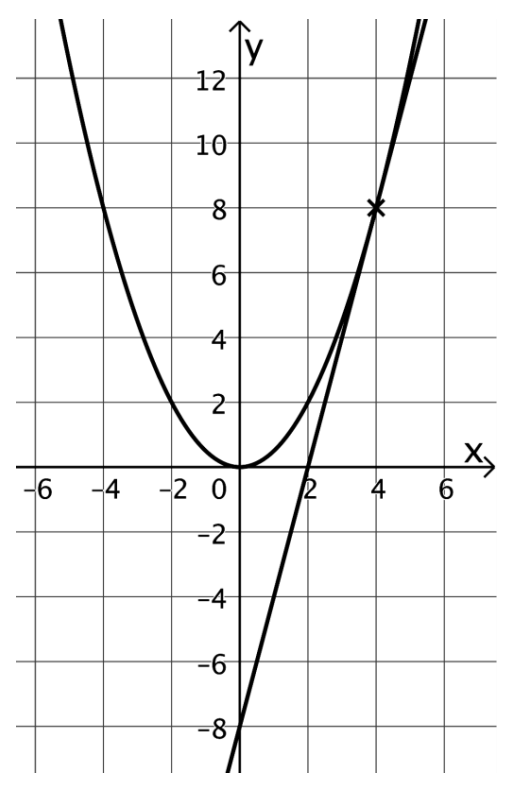
1. Geben Sie anhand der Abbildung eine Gleichung der Tangente 𝑡 an. [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Gleichung der Tangente t
  Tangente an Graph
  $t : y = m \cdot x + b$
  Der y-Achsenabschnitt ist $b = - 8$ (Schnitt von $t$ mit der y-Achse).
  Mit dem eingezeichneten Steigungsdreieck erhält man $m = \frac{Δ y}{Δ x} = \frac{16}{4} = 4$ .
  Also ist $t : y = 4 \cdot x - 8$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt $t : y = m \cdot x + b$ .
  Lies den y-Achsenabschnitt $b$ ab.
  Zeichne ein passendes Steigungsdreieck ein und bestimme $m$ .
2. Weisen Sie nach, dass für jeden Wert $u \in ℝ$ die Tangente an den Graphen von $f_{a}$ im Punkt $(u | f_{a} (u))$ die 𝑦-Achse im Punkt $(0 | - 𝑓_{𝑎} (𝑢))$ schneidet. [4 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Tangente an den Graphen von $f_{a}$ im Punkt $(u | f_{a} (u))$ schneidet die y-Achse im Punkt $(0 | - f_{a} (u))$
  Es ist $f_{a} (x) = a x^{2} \Rightarrow f_{a}^{'} (x) = 2 a x$ und der Punkt ist $(u | f_{a} (u))$ .
  $\Rightarrow f_{a}^{'} (u) = 2 a u = m_{T}$
  Weiterhin gilt für die Tangente:
  $t : y = m_{T} \cdot x + b = 2 a u \cdot x + b$
  Setze die Koordinaten von $(u | f_{a} (u))$ in $t : y = 2 a u \cdot x + b$ ein:
  $t : f_{a} (u) = 2 a u \cdot u + b \Rightarrow b = f_{a} (u) - 2 a u^{2}$
  Mit $f_{a} (u) = a u^{2}$ folgt dann für $b = a u^{2} - 2 a u^{2} = - a u^{2}$
  Damit erhält man für die Tangentengleichung im Punkt $(u | f_{a} (u))$ :
  $t : y = 2 a u \cdot x - a u^{2}$
  Für den Schnittpunkt der Tangente $t$ mit der y-Achse setze $x = 0$ in $t$ ein:
  $t : y = 2 a u \cdot x - a u^{2}$ mit $x = 0$ folgt $y = - a u^{2} = - f_{a} (u)$
  Also ist:
  $S_{y} (0 | - f_{a} (u))$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Gleichung der Tangente für $f_{a} (x)$ im Punkt $(u | f_{a} (u))$ .
  Setze $x = 0$ in die Tangentengleichung ein, um den Schnittpunkt mit der y-Achse zu bekommen.
6
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q2
Für eine Zahl $𝑎 > 0$ zeigt die Abbildung den Graphen $𝐺_{𝑓}$ der in $ℝ$ definierten Funktion $f$ mit $f (𝑥) = x^{3} - 2 a x^{2} + a^{2} x$ sowie die Gerade $h$ . $𝐺_{𝑓}$ und $ℎ$ schneiden sich im Koordinaten-ursprung und $ℎ$ verläuft senkrecht zur Tangente an $𝐺_{𝑓}$ im Koordinatenursprung. Zudem berühren sich $𝐺_{𝑓}$ und die x-Achse im Punkt $(𝑎 | 0)$ .
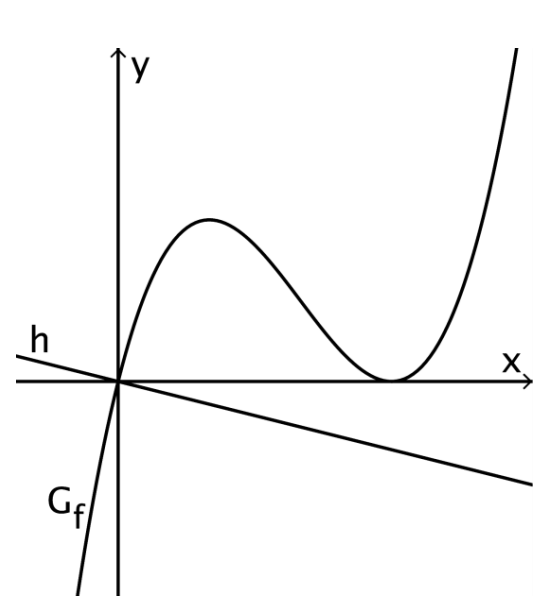
Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
Die beiden gemeinsamen Punkte von $𝐺_{𝑓}$ und der x-Achse sind zwei benachbarte Eckpunkte des Rechtecks.
Eine Diagonale liegt auf der Gerade $h$ .
Skizzieren Sie das Rechteck in der Abbildung und zeigen Sie, dass der Flächeninhalt des Rechtecks unabhängig von $𝑎$ ist. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Skizziere das Rechteck in der Abbildung
Eingezeichnetes Rechteck
Anmerkung: Zusätzlich (in der Aufgabenstellung nicht verlangt) wurde auch die Tangente $t_{f}$ eingezeichnet.
Zeige, dass der Flächeninhalt des Rechtecks unabhängig von $𝑎$ ist
Für den Flächeninhalt des Rechtecks wird die Gleichung der Tangente $h$ benötigt.
Gegeben ist $f (𝑥) = x^{3} - 2 a x^{2} + a^{2} x$ .
Für die Tangentengleichung $h$ muss $f^{'} (0)$ berechnet werden.
$f^{'} (x) = 3 x^{2} - 4 a x + a^{2} \Rightarrow f^{'} (0) = a^{2}$
Die Steigung $m_{t_{f}}$ der Tangente $t_{f}$ im Koordinatenursprung ist gleich $a^{2}$ .
Da $h$ senkrecht zur Tangente $t_{f}$ an $𝐺_{𝑓}$ im Koordinatenursprung steht, gilt:
$m_{h} ⟂ m_{t_{f}} \Rightarrow m_{h} \cdot m_{t_{f}} = - 1 \Rightarrow m_{h} = \frac{- 1}{a^{2}}$
Dann gilt für die Tangentengleichung $h$ :
$h : y = - \frac{1}{a^{2}} \cdot x$
Der Berührpunkt von $G_{f}$ und der x-Achse ist der Punkt $(a | 0)$ .
Die Länge der Grundseite $g$ des Rechtecks ist also gleich $a$ .
Die Höhe des Rechtecks $h$ ist $| h (a) |$ .
$h (a) = - \frac{1}{a^{2}} \cdot a = - \frac{1}{a} \Rightarrow | h (a) | = \frac{1}{a}$
Dann gilt für den Flächeninhalt des Rechtecks:
$A = g \cdot h = a \cdot \frac{1}{a} = 1$
Der Flächeninhalt des Rechtecks ist unabhängig von $𝑎$ .
Teil 1
Zeichne das Rechteck in die Abbildung ein. Beachte dabei, dass die beiden gemeinsamen Punkte von $𝐺_{𝑓}$ und der x-Achse zwei benachbarte Eckpunkte des Rechtecks sind und dass eine Diagonale des Rechtecks auf der Geraden $h$ liegt.
Teil 2
Bestimme die Gleichung der Tangente $t_{f}$ im Koordinatenursprung. Beachte, dass $ℎ$ senkrecht zur Tangente $t_{f}$ an $𝐺_{𝑓}$ im Koordinatenursprung verläuft.
Mit der Gleichung von $h$ kann dann der Flächeninhalt des Rechtecks berechnet werden.
7
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q3
Gegeben ist der Graph, der die kumulierten
Wahrscheinlichkeiten $𝑃 (𝑋 \leq 𝑘)$ für eine
normalverteilte Zufallsgröße $𝑋$ darstellt.
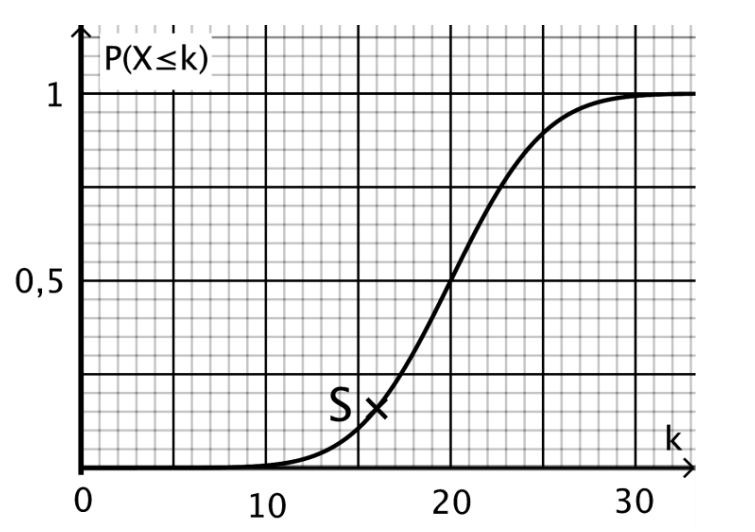
1. Begründen Sie, dass gilt: $μ = 20$ . [1 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Begründe, dass gilt: $μ = 20$
  Aus der Abbildung kann abgelesen werden:
  $P (\leq 20) = 0,5$
  Andererseits gilt: $P (X \leq x) \approx Φ (\frac{x - μ}{σ})$
  Also ist hier: $Φ (\frac{20 - μ}{σ}) = 0,5$
  Es gilt weiterhin:
  $Φ (0) = 0,5 \Rightarrow \frac{20 - μ}{σ} = 0 \Rightarrow μ = 20$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies $P (X \leq 20)$ aus der Abbildung ab.
  Weiterhin gelten: $P (X \leq x) \approx Φ (\frac{x - μ}{σ})$ und $Φ (0) = 0,5$ .
2. Der Punkt $S$ liegt auf dem Graphen und hat die Koordinaten $𝑆 (16 | 0,16)$ .
  Bestimmen Sie einen Näherungswert für $P (μ - 1,5 σ \leq 𝑋 \leq μ + 1,5 σ)$ . [4 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Bestimme einen Näherungswert für $P (μ - 1,5 σ \leq X \leq μ + 1,5 σ)$
  Benötigt wird der Wert von $σ$ .
  Gegeben ist der Punkt $S (16 | 0,16)$ und aus Aufgabe a) $μ = 20$ .
  Demnach gilt: $P (X \leq 16) = 0,16$ .
  Also ist $Φ (\frac{16 - 20}{σ}) = 0,16$ .
  Das Argument von $Φ$ ist negativ:
  $Φ (- z) = 1 - Φ (z) = 0,16 \Rightarrow Φ (z) = 0,84 \Rightarrow z = 1$
  Mit $z = \frac{4}{σ}$ und $z = 1 \Rightarrow σ = 4$
  Setze nun $μ = 20$ und $σ = 4$ in $P (μ - 1,5 σ \leq X \leq μ + 1,5 σ)$ ein:
  $P (20 - 1,5 \cdot 4 \leq X \leq 20 + 1,5 \cdot 4) = P (14 \leq X \leq 26)$
  Aus der Abbildung liest man ab:
  $P (14 \leq X \leq 26) = P (X \leq 26) - P (X \leq 14) \approx 0,93 - 0,07 = 0,86$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gilt: $P (X \leq 16) = 0,16$ .
  Weiterhin gilt dann: $Φ (\frac{16 - 20}{σ}) = 0,16$ .
  Beachte $Φ (- z) = 1 - Φ (z)$ . Dann kann $σ$ berechnet werden.
  Setze den berechneten Wert von $σ$ und den berechneten Wert von $μ$ aus Aufgabe a) in $P (μ - 1,5 σ \leq X \leq μ + 1,5 σ)$ ein und vereinfache.
  Die entsprechenden Wahrscheinlichkeiten können aus der Abbildung abgelesen werden.
8
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q4
Betrachtet wird ein Tetraeder, bei dem die Seiten mit den Zahlen 1 bis 4 durchnummeriert sind. Beim Werfen des Tetraeders werden alle Zahlen mit gleicher Wahrscheinlichkeit erzielt. Das Tetraeder wird viermal geworfen. Die Zufallsgröße $𝑋$ beschreibt die Anzahl der Würfe, bei denen die Zahl 1 erzielt wird. Die Wahrscheinlichkeitsverteilung von $𝑋$ ist in Abbildung 1 dargestellt.
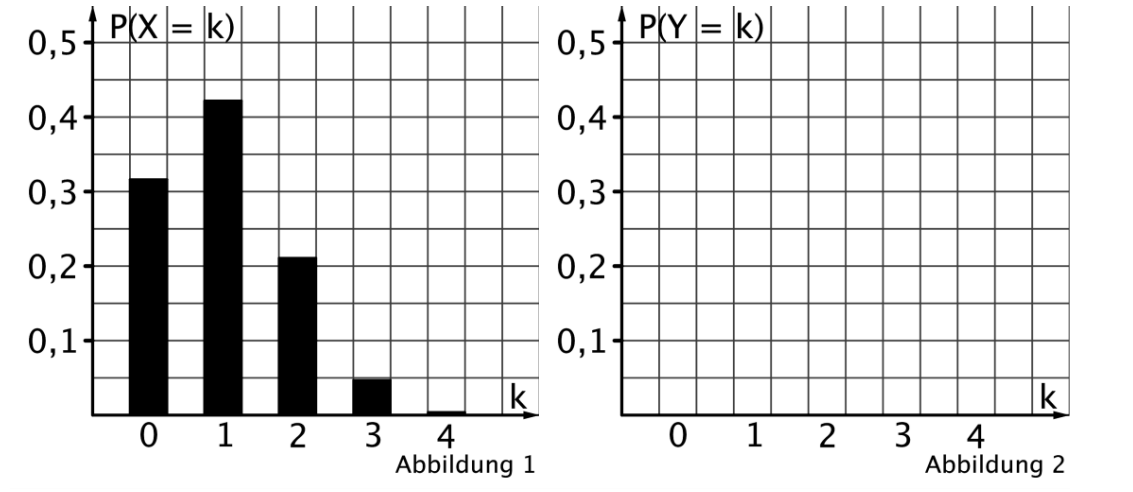
1. Die Zufallsgröße $𝑌$ gibt die Anzahl der Würfe an, bei denen die Zahl 1 nicht erzielt wird.
  Stellen Sie die Wahrscheinlichkeitsverteilung von $𝑌$ in Abbildung 2 dar. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Stelle die Wahrscheinlichkeitsverteilung von $𝑌$ in Abbildung 2 dar
  Die Zufallsgröße $𝑋$ beschreibt die Anzahl der Würfe, bei denen die Zahl 1 erzielt wird. Die Zufallsgröße $𝑌$ gibt die Anzahl der Würfe an, bei denen die Zahl 1 nicht erzielt wird.
  $X = 0$ entspricht $Y = 4$ , $X = 1$ entspricht $Y = 3$ usw.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $X = 0$ entspricht $Y = 4$ , $X = 1$ entspricht $Y = 3$ usw.
2. Bei einem anderen Zufallsexperiment werden ein roter und ein grüner Würfel, bei denen die Seiten jeweils mit den Zahlen 1 bis 6 durchnummeriert sind, viermal gleichzeitig geworfen. Geben Sie zu diesem Zufallsexperiment eine Zufallsgröße $𝑍$ an, die die gleiche Wahrscheinlichkeitsverteilung hat wie $𝑋$ , und begründen Sie Ihre Angabe. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Gib zu diesem Zufallsexperiment eine Zufallsgröße $𝑍$ an, die die gleiche Wahrscheinlichkeitsverteilung hat wie $𝑋$ , und begründe Deine Angabe
  Die Wahrscheinlichkeit für eine Zahl beim Tetraeder ist $p = \frac{1}{4}$ .
  Gesucht ist also ein Würfelexperiment mit zwei Würfeln, bei dem die Wahrscheinlichkeit ebenfalls $\frac{1}{4}$ ist.
  Die Zufallsgröße $Z$ beschreibt die Anzahl der Würfe, bei denen keine der beiden erzielten Zahlen größer als drei ist.
  Es gibt unter den insgesamt 36 gleichwahrscheinlichen Ergebnissen genau 9, bei denen keine der beiden erzielten Zahlen größer als 3 ist.
  Die Wahrscheinlichkeit für das Ereignis „Keine der beiden erzielten Zahlen ist größer als drei.“ beträgt somit $\frac{9}{36} = \frac{1}{4}$
  Damit sind die beiden Zufallsgrößen $X$ und $Z$ binomialverteilt, mit den Parametern $p = \frac{1}{4}$ und $n = 4$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Wahrscheinlichkeit für eine Zahl beim Tetraeder ist $p = \frac{1}{4}$ .
  Suche also ein Würfelexperiment mit zwei Würfeln, bei dem die Wahrscheinlichkeit ebenfalls $\frac{1}{4}$ ist.
9
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe Q5
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung).
Die Eckpunkte $A, B, C$ und $D$ des Oktaeders liegen in der Ebene $H$ mit der Gleichung $2 𝑥_{1} + 𝑥_{2} + 2 𝑥_{3} = 6$ .
Es gilt: $𝐴 (1 | 2 | 1)$ und $𝐶 (- 3 | - 6 | 9)$ .
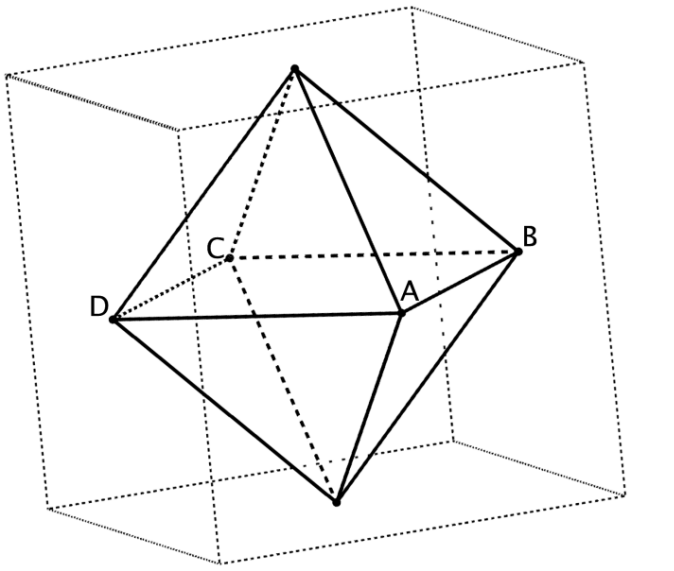
1. Weisen Sie nach, dass die Kantenlänge des Würfels $12$ beträgt. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
  Die Kantenlänge des Würfels soll 12 betragen
  Berechne den Betrag des Vektors $\vec{A C}$ .
  $\vec{A C} = \vec{O C} - \vec{O A} = (\begin{array}{c} - 3 \\ - 6 \\ 9 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) = (\begin{array}{c} - 4 \\ - 8 \\ 8 \end{array})$
  $| \vec{A C} | = \sqrt{(- 4)^{2} + (- 8)^{2} + 8^{2}} = \sqrt{16 + 64 + 64} = \sqrt{144} = 12$
  Die Kantenlänge des Würfels beträgt $12 LE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Betrag des Vektors $\vec{A C}$ .
2. Bestimmen Sie die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in $𝐻$ liegen. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalenvektor – Umwandeln von Ebenendarstellungen
  Die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in H liegen
  Die Spitze $S$ der oberen Pyramide liegt senkrecht über dem Mittelpunkt von $A C$ .
  $\vec{O M_{A C}} = \frac{1}{2} (\vec{O A} + \vec{O C}) = \frac{1}{2} (\begin{array}{c} 1 - 3 \\ 2 - 6 \\ 1 + 9 \end{array}) = \frac{1}{2} (\begin{array}{c} - 2 \\ - 4 \\ 10 \end{array}) = (\begin{array}{c} - 1 \\ - 2 \\ 5 \end{array})$
  Weiterhin kann der Normalenvektor der Ebene $H$ abgelesen werden:
  ${\vec{n}}_{H} = (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})$
  Sein Betrag ist $| {\vec{n}}_{H} | = \sqrt{2^{2} + 1^{2} + 2^{2}} = \sqrt{4 + 1 + 4} = \sqrt{9} = 3$ .
  Da die Kantenlänge des Würfels $12$ ist, ist die Höhe einer Pyramide gleich $6$ .
  Da der Betrag des Normalenvektors $3$ beträgt, muss er zweimal zum Vektor $\vec{O M_{A C}}$ addiert werden, um zur Pyramidenspitze $S$ zu gelangen ( $h = 6 = 2 \cdot | {\vec{n}}_{H} |$ ).
  Dann folgt für den Vektor $\vec{O S}$ :
  $\vec{O S} = \vec{O M_{A C}} + 2 \cdot {\vec{n}}_{H} = (\begin{array}{c} - 1 \\ - 2 \\ 5 \end{array}) + 2 \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} - 1 + 4 \\ - 2 + 2 \\ 5 + 4 \end{array}) = (\begin{array}{c} 3 \\ 0 \\ 9 \end{array})$
  Der eine Eckpunkt $S$ des Oktaeders hat die Koordinaten $S (3 | 0 | 9)$ .
  Ergänzung (nicht in der Aufgabenstellung gefordert):
  Der andere Eckpunkt $S^{'}$ , der nicht in $H$ liegt, ist dann:
  $\vec{O S^{'}} = \vec{O M_{A C}} - 2 \cdot {\vec{n}}_{H} = (\begin{array}{c} - 1 \\ - 2 \\ 5 \end{array}) - 2 \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} - 1 - 4 \\ - 2 - 2 \\ 5 - 4 \end{array}) = (\begin{array}{c} - 5 \\ - 4 \\ 1 \end{array})$
  Der andere Eckpunkt des Oktaeders $S^{'}$ hat die Koordinaten $S^{'} (- 5 | - 4 | 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Mittelpunkt von $A C$ $\Rightarrow \vec{O M_{A C}}$
  Lies den Normalenvektor der Ebene $H$ ab und berechne seinen Betrag.
  Da die Kantenlänge des Würfels $12$ ist, ist die Höhe einer Pyramide gleich $6$ .
  Überlege Dir, wie oft der Normalenvektor zum Vektor $\vec{O M_{A C}}$ addiert werden muss, um die Spitze $S$ der oberen Pyramide zu erreichen.
10
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
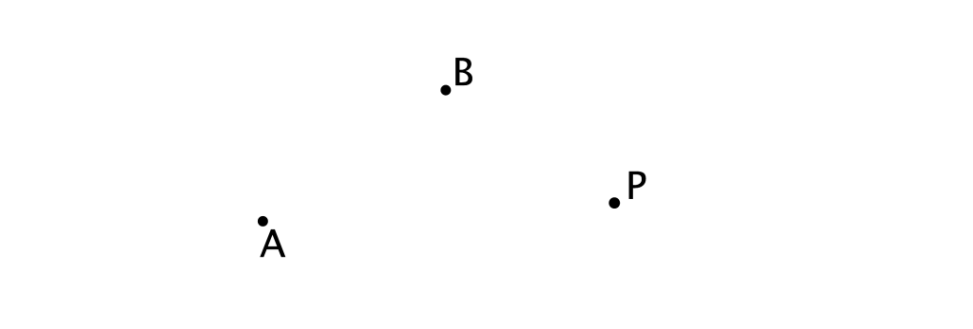
Aufgabe Q6
Die Abbildung zeigt die Punkte $A, B$ und $P$ . Die Ebene, in der die drei Punkte liegen, wird durch die Zeichenebene dargestellt.
Betrachtet werden Geraden $𝑔, 𝑔^{*}$ und $h$ , für die gilt:
$g$ verläuft durch $A$ , $g^{*}$ durch $B$ und $h$ durch $P$ .
$g$ und $g^{*}$ schneiden sich in $P$ .
Wird $g$ an $h$ gespiegelt, so entsteht $g^{*}$ .
Zeichnen Sie die Gerade $g$ , die Gerade $g^{*}$ und eine Gerade $ℎ$ in die Abbildung ein.
Geben Sie einen Term an, mit dem aus den gegebenen Punkten $𝐴$ , $𝐵$ und $𝑃$ der Ortsvektor eines weiteren Punktes von $ℎ$ bestimmt werden kann. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Geraden
Zeichne die Gerade $𝑔$ , die Gerade $𝑔^{*}$ und eine Gerade $ℎ$ in die Abbildung ein
Gib einen Term an, mit dem aus den gegebenen Punkten $𝐴$ , $𝐵$ und $𝑃$ der Ortsvektor eines weiteren Punktes von $ℎ$ bestimmt werden kann
Die gesuchte Gerade $h$ ist Winkelhalbierende im Schnittpunkt $P$ der Geraden $g$ und $g^{*}$ . Für diese Winkelhalbierende gibt es zwei Möglichkeiten, die beispielhaft in den beiden Lösungsvarianten eingezeichnet sind.
Es werden zwei Möglichkeiten zur Konstruktion eines Punktes $D$ auf $h$ angegeben.
Lösungsmöglichkeit 1
Skizze zur Veranschaulichung:
Finde einen Punkt $C$ auf der Geraden $g$ , der an $h$ gespiegelt den Punkt $B$ ergibt.
Dabei gilt: $| \vec{B P} | = | \vec{P C} |$ und $\vec{P C} = \frac{| \vec{B P} |}{| \vec{A P} |} \cdot \vec{A P}$
Addiert man zum Vektor $\vec{O B}$ den Vektor $\vec{P C}$ kommt man zu einem Punkt $D$ auf der Geraden $h$ :
Das Viereck $B P C D$ ist eine Raute, da alle Seiten gleich lang sind (die Seite $C D$ entsteht ja durch Verschiebung von $B P$ ) und die Gerade $h$ durch $P$ und $C$ ist als Diagonale eine Symmetrieachse.
Der gesuchte Term ist also:
$\vec{O B} + \frac{| \vec{B P} |}{| \vec{A P} |} \cdot \vec{A P}$
Lösungsmöglichkeit 2
Konstruiere einen Punkt $C$ auf der Strecke von $A$ nach $P$ , der denselben Abstand zu $P$ wie $B$ hat.
Der Mittelpunkt von $B$ und $C$ liegt dann auf der Geraden $h$ .
Finde einen Punkt $C$ auf der Geraden $g$ , der an $h$ gespiegelt den Punkt $B$ ergibt.
Dabei gilt: $| \vec{B P} | = | \vec{P C} |$ und $\vec{P C} = \frac{| \vec{B P} |}{| \vec{P A} |} \cdot \vec{P A}$
Addiert man zum Vektor $\vec{O C}$ die Hälfte des Vektors $\vec{C B}$ kommt man zu einem Punkt $D$ auf der Geraden $h$ .
Der gesuchte Term ist also:
$\vec{O C} + \frac{1}{2} \cdot \vec{C B} = \vec{P C} + \vec{O P} + \frac{1}{2} \cdot \vec{C B} = \frac{| \vec{B P} |}{| \vec{P A} |} \cdot \vec{P A} + \vec{O P} + \frac{1}{2} \cdot \vec{C B}$
Der Vektor $\vec{C B}$ muss noch umgeformt werden:
$\frac{1}{2} \cdot \vec{C B} = \frac{1}{2} (\vec{O B} - \vec{O C}) = \frac{1}{2} (\vec{O B} - (\vec{P C} + \vec{O P})) = \frac{1}{2} (\vec{O B} - \vec{O P} - \vec{P C})$
$\frac{1}{2} (\vec{O B} - \vec{O P} - \vec{P C}) = \frac{1}{2} (\vec{P B} - \vec{P C}) = \frac{1}{2} (\vec{P B} - \frac{| \vec{B P} |}{| \vec{P A} |} \cdot \vec{P A})$
Damit erhält man:
$\frac{| \vec{B P} |}{| \vec{P A} |} \cdot \vec{P A} + \vec{O P} + \frac{1}{2} \cdot (\vec{P B} - \frac{| \vec{B P} |}{| \vec{P A} |} \cdot \vec{P A})$
Zusammengefasst:
$\vec{O P} + \frac{1}{2} \cdot \vec{P B} + \frac{1}{2} \cdot \frac{| \vec{B P} |}{| \vec{P A} |} \cdot \vec{P A}$
Teil 1
Zeichne die Gerade $g$ durch die Punkte $A$ und $P$ .
Zeichne die Gerade $g^{*}$ durch die Punkte $B$ und $P$ .
Spiegele die Gerade $g$ an $h$ .
Teil 2
Finde einen Punkt $C$ auf der Geraden $g$ , der an $h$ gespiegelt den Punkt $B$ ergibt.
Berechne den Vektor $\vec{P C}$ .