Aufgabe Q5
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung).
Die Eckpunkte und des Oktaeders liegen in der Ebene mit der Gleichung .
Es gilt: und .
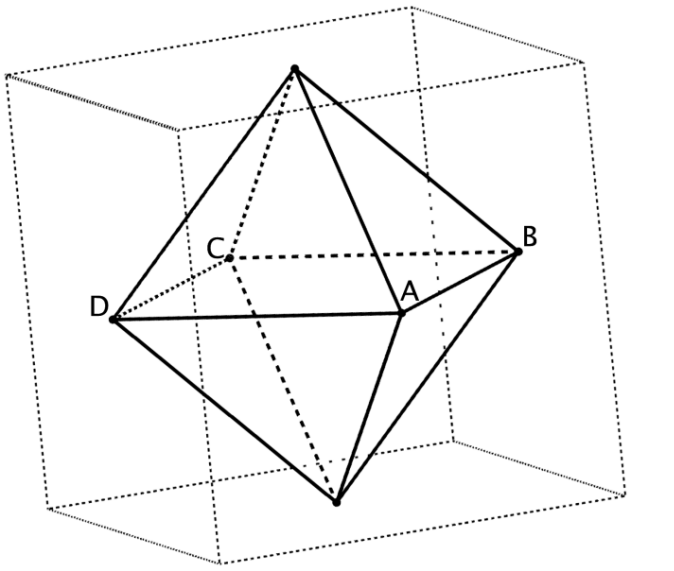
Weisen Sie nach, dass die Kantenlänge des Würfels beträgt. [2 BE]
Bestimmen Sie die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in liegen. [3 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
serlo.orgDieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
→ Was bedeutet das?